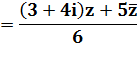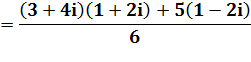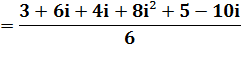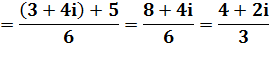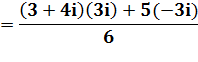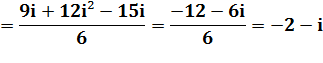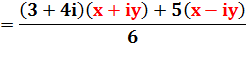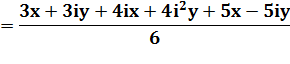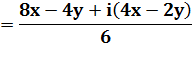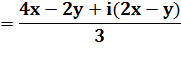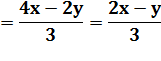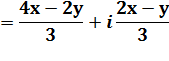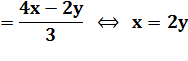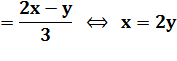|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres complexes Exercices de terminale Problèmes relevés dans les
annales du baccalauréat et résolus à ma manière. |
Données communes
|
Plan
et repère orthonormé Deux
nombres complexes: z = a
+ ib,
affixe d'un point M (ou du vecteur z'
= a' + ib', affixe d'un point M' (ou du vecteur À
tout point M (affixe z) du plan, on associe le point M' (affixe z'). |
|
|
|||
|
Application f |
|
|
|
|
Soit les trois points A, B
et C |
Affixes A, B et C |
zA
= 1+2i; zB
= 1; zC
= 3i. |
|
|
Point A' image de A |
Affixe A' |
|
|
|
Point B' image de B |
Affixe B' |
|
|
|
Point C'
image de C |
Affixe C' |
|
|
|
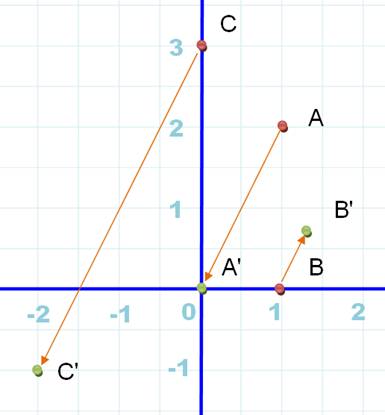
Graphe |
|
||
|
Exercice 12 – Écriture algébrique
|
|
|||
|
Application f |
|
|
||
|
Avec z = x + iy |
|
|
||
|
Séparez partie réelle et
partie imaginaire. |
|
|
Re(z)
= 2 Im(z) |
|
|
|
|||
|
Invariants |
|
Tout point M tel que son image M' = M |
|
|
Affixe de z = affixe de z' |
|
|
|
|
Égalité en x (Réels) |
|
|
|
|
Égalité en y (Imaginaires) |
|
Même relation |
|
|
C'est l'équation d'une droite
|
|
|
|
|
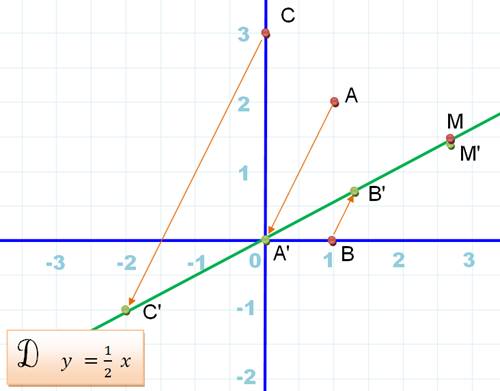
Graphe On remarque que les points
images de A, B et C appartiennent à la droite des invariants. Pour tout point M l'affixe
de l'image M' est un nombre dont la partie réelle
est le double de la partie imaginaire. Ce qui correspond bien à la droite D. Le lieu des points images M' est la droite D. |
Tout point du plan a pour image un point de
la droite D. |
||
|
|
|||
|
Un nombre complexe |
|
|
|
|
Calculez l'expression et
simplifiez le plus possible. |
|
|
|
|
Exercice 22 – Cercle et rotation
|
|
||
|
Point A |
A (2; 0) |
zA
= 2+ 0.i = 2 |
|
|
Deux points B et B' |
Affixes |
|
|
|
Cercle |
Centre O |
Rayon = 2 |
|
|
B et B' ont même module 2 et
ils appartiennent au cercle |
|
|
|
|
Soit D appartenant au cercle
et son affixe exponentielle |
|
le module est 2 et l'argument (angle) est thêta. |
|
|
Positionnez le point E définit
par: |
|
L'exponentielle correspond à une rotation
de Pi/3 = 60° |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/Exerc01.htm
|
![]()