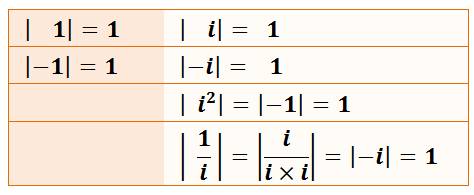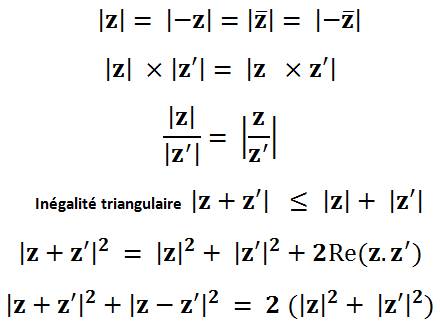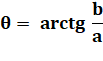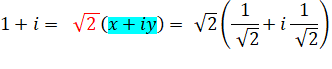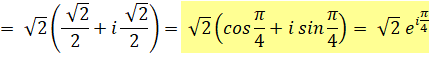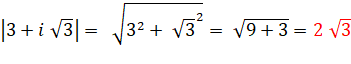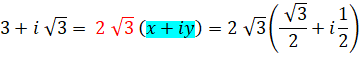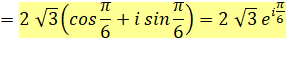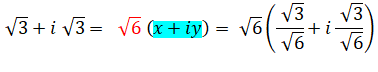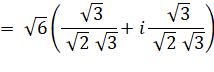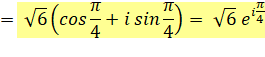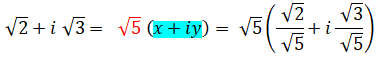|
||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres complexes Forme polaire |
|
|
|
|
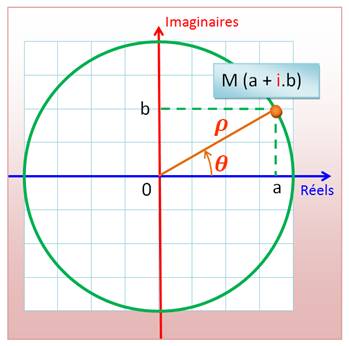
un nombre complexe sous sa forme polaire s'écrit:
|
|
|
|
|
|
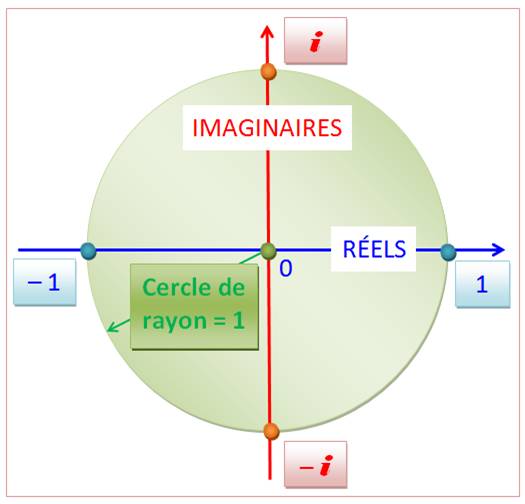
Tous les nombres complexes dont l'image est située sur
le cercle de rayon unité ont un module unité.
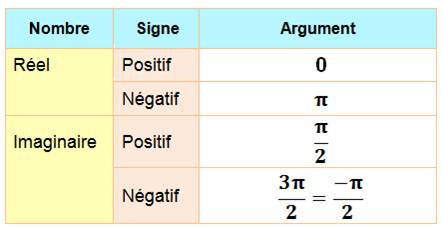
Quelques valeurs
typiques
|
|
Voir Exemple
de calculs de modules / U le groupe des unités
sur C / Morphisme
|
|
|
|
Module
Argument Arg(z . z') = Arg(z)
+ Arg(z') Arg(z / z') = Arg(z) – Arg(z')
Voir Angles |
|
|
|
||
|
Module Argument |
|
|
|
Partie réelle Partie imaginaire |
a = b = |
|
|
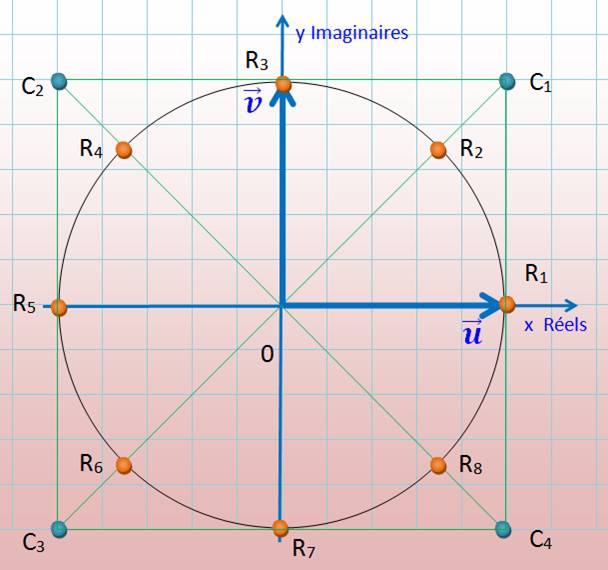
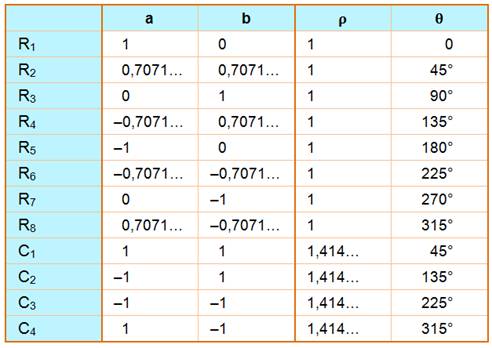
u et v
sont les vecteurs unitaires portés par les deux axes Valeurs des nombres
complexes indiqués sur cette figure:
|
||
|
|
||
|
1 + i |
Notez l'astuce qui
consiste à poser x = cos et y = sin, puis, à trouver leur valeur en les égalant
avec la partie réelle et la partie imaginaire du nombre de départ. |
|
|
3 + i |
|
|
|
|
Vérification: ce
nombre est bien un multiple du premier nombre calculé (1 + i). |
|
|
|
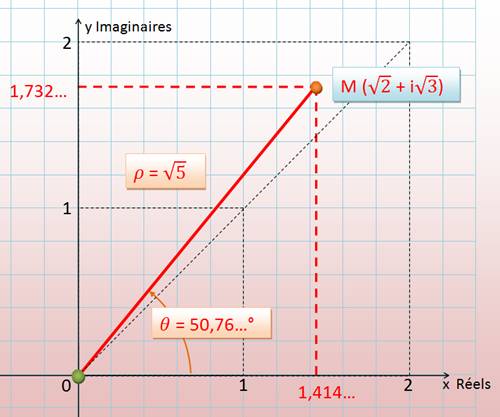
Calcul: le nombre
0886 radians = 50,76…° est donné par une calculette ou tableur ou programme
mathématique. |
|
Illustration de ce
dernier cas
|
|
La forme
polaire de l'ours

![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/Polaire.htm |
![]()