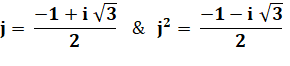|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
|
||
|
On
introduit le nombre imaginaire: tel que i² = – 1 Voir Nombres complexes et racines
de nombres négatifs |
Exemple (Identités
remarquables) a² – b² = (a – b) (a + b) a² + b² = (a – b |
|
|
Formés
avec des nombres entiers, ils ont un comportement proche de ceux des nombres entiers. Notez
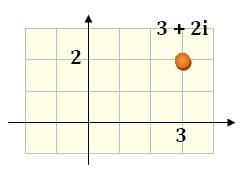
qu'en représentation géométrique des nombres complexes,
les nombres entiers de Gauss sont ceux qui sont aux nœuds du quadrillage des
nombres entiers en abscisse comme en ordonnée. |
Les
nombres de la forme a + b avec
a et b entiers sont
décomposables de façon unique en nombres complexes non décomposables
eux-mêmes (facteurs premiers).
|
|
|
|
5
= 2² + 1² = ( 2 – 8
= 2² + 2² = ( 2 – 2 10 = 3² + 1² = ( 3 – 13 = 3² + 2² = ( 3 – 2 |
|
|
Comme on vient de la voir, c'est le cas de tous les
nombres qui sont somme de deux carrés. |
3 non 5 oui => 5 = ( 2 – 7 non 11 non 13 oui => 13 =
( 3 – 2 Etc. |
|
|
|
|
|
Soit un cercle
centré sur l'origine des axes et de rayon
|
|
|
|
||
|
|
a + i · b nombres
de Gauss. a + j · b nombres
d'Eisenstein. Avec
a et b des nombres entiers. Attention: pour éviter la confusion avec le symbole de l'intensité (I), les électroniciens
remplacent le i des imaginaires par j (à ne pas confondre avec le j des
mathématiciens) |
|
|
Notez: puissance trois |
Somme
de deux cubes a3
+ b3 = (a + b) (a² – ab
+ b²) = (a + b) (a + jb)
(a + j²b) 35 = 23 +
33 = 5 x 7 = 5 (2 + i |
|
|
|
||
Gotthold Eisenstein (1823/1852) – Mort à moins de 30 ans
de tuberculose
|
|
||
|
|
a + i .
b nombres de Gauss a + j .
b nombres d'Eisenstein a + |
|
|
|
Puissances n an
+ bn avec |
|
|
|
||
|
Lorsque
le nombre somme de deux carré est
lui-même un carré nous avons à faire aux triplets
de Pythagore |
Somme de deux carrés a²
+ b² = (a – b a²
+ b² = c² 3² + 4² = 5² |
|
|
|
Théorème de
Fermat-Wiles an
+ bn = cn Cette
équation n'a pas de solution en nombres entiers pour n > 2 (a,
b, c non nuls) |
|
|
|
an + bn
= cn = (a + Contrairement
aux entiers ordinaires et aux entiers de Gauss, ces nombres en a + |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()
![]()
Calcul avec les deux
méthodes
![]() en nombres entiers classiques (toute
somme de trois cubes est le produit de deux nombres)
en nombres entiers classiques (toute
somme de trois cubes est le produit de deux nombres)
![]() avec les nombres complexes (seul
intérêt de montrer la factorisation en trois termes)
avec les nombres complexes (seul
intérêt de montrer la factorisation en trois termes)

Retour >>>
Nombre 35
![]()