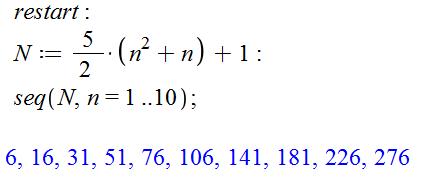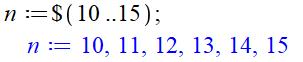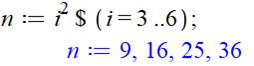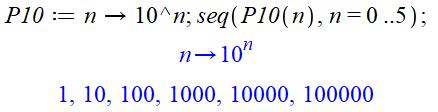Programmation suite, séquence

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/04/2020 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Informatique
Débutants Programmation	Programmation			Glossaire Algorithme
INDEX Programmation Algorithmes Multimédia	<<< Division	Séquence	Liste >>>
		Sommaire de cette page >>> Définir une séquence >>> Manipuler une séquence >>> Cumul addition >>> Cumul sommes littérales >>> Cumul multiplications >>> Astuce >>> Bilan

SÉQUENCE ou SUITE

Comment faciliter l'écriture de suite de nombres, de mots …?

Comment facilement calculer des cumuls sur des sommes ou des produits ou …?

Remarque: En français il faudrait dire SUITE, mais Mapple utilise le type SÉQUENCE

Définir une séquence
Deux possibilités: avec le symbole $ ou avec le mot "seq". Dans les deux cas, on donne la valeur littérale de la fonction (ici: i) et l'extension de la séquence (ici, i varie de 1 à 4).		> i $ i=1..4; > seq(i,i=1..4);
Voici un autre exemple, montrant comment obtenir la séquence des nombres carrés. L'accent circonflexe veut dire puissance: i^2 = i².		> i^2 $ i=1..4; > seq(i^2,i=1..4);
Pratique pour calculer une formule. Ici, les nombres pentagonaux centrés.

Raccourcis avec $

Une SUITE (ou Séquence) est une succession d'expressions (nombres ou caractères) séparées par une virgule.

Exemple: séquence des puissances de 10

Instruction à recopier dans Maple

P10:=n->10^n; seq(P10(n), n=0..5);

Programme et exécution

Voir Puissances de 10

Manipuler une séquence

Il est possible d'isoler un élément de la séquence en donnant simplement son rang entre crochets.

Ainsi, mercredi (bleu) est bien le troisième élément de la séquence "jours".

Notez: la première séquence est suivie de ";" et la séquence est imprimée (bleu); alors que la seconde est suivie de ":" elle n'est pas imprimée.

> MaSuite:=1,6,7,9,10;

MaSuite[3];

> jours:=lundi, mardi, mercredi,

jeudi, vendredi, samedi,

dimanche:

jours[3];

Il est possible d'isoler plusieurs éléments successifs de la séquence en donnant simplement le rang de départ et celui d'arrivée entre crochets.

> MaSuite:=1, 6, 7, 9, 10, papa,

maman, zut, 27, 123;

MaSuite[3..7];

Il est possible de compter la quantité d'éléments dans une séquence avec l'instruction nops.

Il suffit de donner le nom de la séquence entre crochet.

> MaSuite:= 1,6,7,9,10;

nops([MaSuite]);

> jours:=lundi, mardi, mercredi,
jeudi, vendredi, samedi,

dimanch):
nops([jours]);

Il est possible de concaténer (cat) les éléments d'une séquence pour former un seul élément, un seul nombre.

> MaSuite:= 1,6,7,9,10;

cat(MaSuite);

Cumul addition

L'instruction add permet de faire la somme cumulée d'une fonction.

Ici, nous faisons la somme: 1 + 2 + 3 + 4 + 5 = 15

Puis: 1 + 3 + 5 + 7 + 9 + 11 = 36

> add(n,n=1..5);

> add(2*n+1,n=0..5);

Illustration avec le calcul du cumul des n entiers (S1), des carrés (S2), des cubes (S3), des puissances 4 (S4) et des puissances 5 (S5).

Et cela, pour les nombres de 1 à i (séquence), avec i variant de 1 à 10 (boucle).

Ainsi, à la ligne 4:

Le premier nombre est: i = 4

1¹ + 2¹ + 3¹ + 4¹ = 10

1² + 2² + 3² + 4² = 30
1³ + 2³ + 3³ + 4³ = 100

Etc.

> for i from 1 to 10 do

S1:=add (n,n=1..i):

S2:=add (n^2,n=1..i):

S3:=add (n^3,n=1..i):

S4:=add (n^4,n=1..i):

S5:=add (n^5,n=1..i):

lprint(i, S1, S2, S3,

S4, S5):

od:

1, 1, 1, 1, 1, 1

2, 3, 5, 9, 17, 33

3, 6, 14, 36, 98, 276

4, 10, 30, 100, 354, 1300

5, 15, 55, 225, 979, 4425

6, 21, 91, 441, 2275, 12201

7, 28, 140, 784, 4676, 29008

8, 36, 204, 1296, 8772, 61776

9, 45, 285, 2025, 15333, 120825

10, 55, 385, 3025, 25333, 220825

Entraînement

Vérifiez que la somme des cubes des nombres successifs est égale au carré de la somme des entiers correspondants.

Exemple:

1³ + 2³ + 3³ + 4³ = (1 + 2 + 3+ 4)² = 100

> for n from 1 to 5 do

S3:= add(i^3, i=1..n):

S2:= add(i, i=1..n)^2:

lprint (n,S3,S2):

od:

1, 1, 1

2, 9, 9

3, 36, 36

4, 100, 100

5, 225, 225

Cumul sommes littérales
L'instruction sum produit le même résultat que add, mais avec une syntaxe un peu différente. Son intérêt réside dans le fait qu'il est possible de calculer en littéral. Comme la somme des entiers jusqu'à n, par exemple. Nous demandons la somme S1 des entiers jusqu'à n. La réponse est une expression algébrique. Pour l'arranger un peu, nous demandons si, à tout hasard, il est possible de factoriser cette expression. Oui! et, c'est la forme sympathique sous laquelle nous la connaissons bien	> sum (i, i=1..5); > S1:= sum(i,i=1..n); factor(S1); S1 = ½ n (n+1) La somme des entiers de 1 à n est égale au demi-produit de n par n+1. >>> Exemples 1 + 2 + 3 + 4 = ½ 4 x 5 = 10 1 + 2 +… + 100 = ½ 100 x 101 = 5 050
Nous voyons qu'il est aussi facile de calculer la somme des carrés des entiers de 1 à n. Ou des cubes. Voir suite jusqu'à la puissance 20	> S2:= sum (i^2, i=1..n); factor(S2); > S3:= sum (i^3, i=1..n); factor(S3);

Cumul multiplications

L'instruction mul permet le calcul des multiplications successives à l'instar de l'instruction add.

Avec la multiplication des entiers successifs nous obtenons la factorielle.
Ex: 4! = 1 x 2 x 3 x 4 = 24.

Nous avons mis en œuvre une boucle pour calculer ces factorielles jusqu'à n = 10.

> for n from 1 to 10 do

M:=mul(i,i=1..n):

lprint(n,M):

od:

1, 1

2, 2

3, 6

4, 24

5, 120

6, 720

7, 5040

8, 40320

9, 362880

10, 3628800

Astuce

Comment calculer le sinus de tous les angles multiples de 30° de 0 à 360°?

Créer une séquence qui fait progresser un angle de Pi/6 en le multipliant par un indice qui varie de 0 à 11.

Comme nous l'avons vu, il est possible

> seq(sin(i*Pi/6),i=0..11);

Rappel:

Sin (30°) = 1/2

> Sinusn30 := seq(sin(i*Pi/6),i=0..11);

Sinusn30[3];

Ce que nous avons appris

La définition de séquences permet un automatisme bien appréciable lorsqu'on manipule les nombres.

Nous savons copter le nombre d'éléments dans une séquence et isoler un élément de cette séquence.

Un logiciel mathématique tel que Mapple

Suite	Suites (seq) conditionnelles Liste Calcul des sous-factorielles (exemple de programmation de séquence) Application à l'extraction des chiffres d'un nombre et au retournement d'une liste Application à la recherche des nombres chanceux Application à la recherche des nombres permutés Application à l'énumération des combinaisons Nombres premiers de Stern – Manipulation de séquences
Voir	Menu en en-tête Programmation – Index
Aussi	Programmation – En savoir un peu plus
Site	Apprendre Maple
Cette page	http://villemin.gerard.free.fr/aInforma/06Sequen.htm