|
||||||||||||||||||||||||||||||||||||||||
![]()
|
LOTO traditionnel avec cartons (3/3) Loto familial Quantité de cartons Nous avons vu comment calculer la quantité de configurations des cartons
sans numéros. Il y en a: 733 320. Introduisons les nombres
dans ces configurations. Quelle est alors la quantité
de cartons différents portant des numéros ? |
Anglais: Bingo Lotto Lottery with tickets / Tambola ticket
Notes sur la méthode de calcul
|
1) Le calcul
qui suit prend bien en compte la disparité des
colonnes: 9 nombres en colonne 1 (de 1 à 9), 11 nombres sur la
dernière colonne (de 80 à 90) et 10 nombres sur les sept autres (de d0 à d9,
selon la dizaine). 3) De très nombreux cartons se retrouvent avec
les mêmes nombres. C'est un autre calcul que d'isoler, par exemple,
des jeux de six cartons portant tous les numéros de 1 à 90. |
|
|
||
|
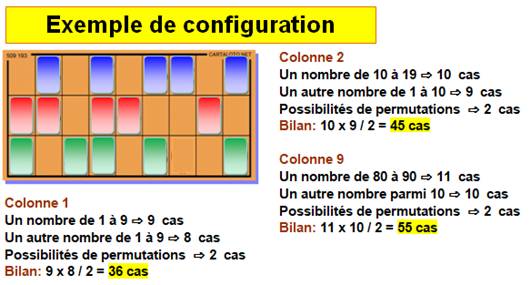
Principe du dénombrement On examine chaque colonne:
|
Exemple avec trois nombres en
colonne 9 Le premier est choisit par 11, le deuxième par mi
10 et le troisième parmi 9. On peut les placer de six manières différentes (a,b,c;
a,c,b; b,a,c; b,c,a; c,a,b; c,b,a). Soit le calcul des possibilités: 11 x 10 x 9 / 6
= 165. Voir Tableau des
neuf cas |
|
|
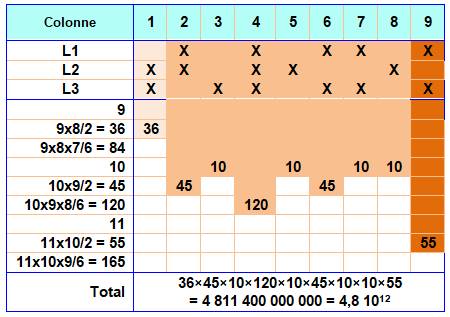
Décompte complet pour une configuration de carton On retrouve bien:
Les choix pour chaque case
sont indépendants, ces valeurs se multiplient. |
|
|
|
5 000 milliards de cartons différents pour une
seule configuration ! |
Estimation En prenant cette
configuration comme une moyenne, avec 150 000
types de congigurations, on a: |
|
Configurations
conduisant au minimum et au maximum de cartons
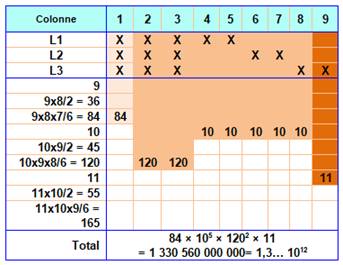
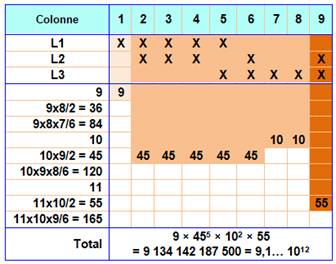
|
|
|||
|
Cas de 1, 2 ou 3 nombres par colonne Compte
tenu des spécificités de chaque configuration de cartons, il est assez
hasardeux de faire un calcul combinatoire. Un programme examinant tous les cas comme vu ci-dessus fera
l'affaire. Le
programme examine chaque configuration et ajoute les sous-totaux trouvés. |
Config = 733 320 Cartons = 3 660 498 857 039 062 500 = 3,66… 1018 Cartons de loto autorisant 1, 2 ou 3 nombres par colonne. Les nombres d'une colonne sont ordonnés du plus petit au plus grand
(on ignore toutes les permutations). |
||
|
Une idée de ce nombre Supposons 10 cartons par millimètre d'épaisseur. |
(3,66 1018) / (10mm x 1000m
x 1000km x 156 000 000Soleil ) = (3,66 1018) / (1,56 1015) =
2 346 Soit une épaisseur de 2 346 fois la distance Terre-Soleil. |
||
|
Cas de 1 ou 2 nombres par colonne Calcul en
supprimant tous les cas des colonnes à trois nombres. |
Cartons = 1 174 751 160 876 562 500 = 1,17… 1018 Cartons de loto autorisant seulement 1 ou 2 nombres par colonne. |
|
|
Vu sur Internet Autres règles du jeu ? |
Cartons = 6,08… 1015 Cartons
= 3,54… 1021 |
|
|
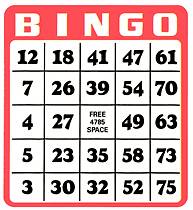
Cas du Bingo 5 x 5 avec 75 nombres (États-Unis) Voir Règles
du Bingo Calcul combinatoire plus facile: 15 nombres
possibles dans les cases des colonnes (1 à 15, puis 16 à 30, etc.) Colonnes BI
GO: 15 x 14 x 13 x 12 x 11 = 360 360 Colonne
N : 15 x 14 x 13 x 12 =
32 760 Q = 360 3604 x 32 760 = 552
446 474 061 128 648 601 600 000 |
Cartons
= 5,52… 1026
|
|
![]()
|
|
||
|
|
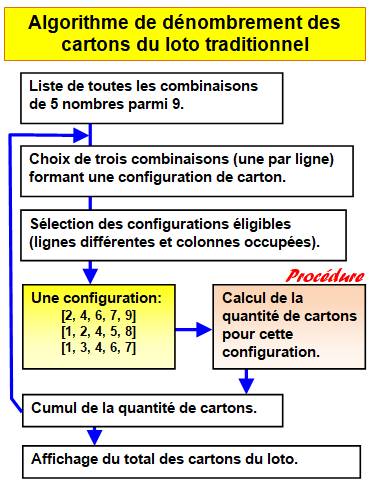
Description La configuration d'un carton est
représentée par la liste des numéros de colonnes occupées. Par exemple: [2,
4, 6, 7, 9] [1,
2, 4, 5, 8] [1,
3, 4, 6, 7] Ces configurations sont obtenues en
listant toutes des combinaisons de 5
nombres parmi 9, et cela trois fois. Soit 1263 = 2 000 376
configurations. Les configurations avec lignes identiques sont éliminées; il reste 1
953 000 configurations différentes. Une configuration est éligible si
toutes les colonnes sont occupées. Les neuf numéros de colonne sont présents
parmi les trois listes. Il y a 733 320 configurations éligibles. Pour chaque configuration, on calcule la quantité de cartons avec
numéros: des milliards de cartons par configurations! La quantité est cumulée et affichée en fin d'examen de toutes les
configurations éligibles. |
|
|
Programme Maple
|
Commentaires Une procédure calcule la
quantité de cartons pour une configuration donnée, comme nous venons de le
voir ci-dessus. Les trois listes de cinq chiffres A, B et C sont proposées à l'examen. Chacune
contient les numéros des cases de la configuration à examiner. Pour chaque numéro de 1 à 9, on évalue la
quantité (kt) de cases non vides dans la colonne
de ce numéro. Selon le numéro de la colonne, et sa quantité de
cases, on donne une valeur à t: (9,
36, 84, 10, 45 …) À chaque fois, le total T
en cours de calcul est multiplié par t (cumul multiplicatif). La valeur retournée par la procédure est T, la
quantité de cartons de cette configuration. Le programme principal, identifie
toutes les configurations. Avec les listes L1,
L2 et L3, on sélectionne toutes les combinaisons de 5 parmi 9 (choose)
qui sont placées en P1, P2 et P3. Trois boucles imbriquées (i, j et k) isolent trois combinaisons (un par ligne du
carton) qui sont mémorisées en P, Q et R. Si ces trois combinaisons sont distinctes et
complètes, on incrémente le compteur kt qui donnera la quantité de
configurations, et on appelle la procédure de calcul des cartons pour cette
configuration (Totcar(P,Q,R)). Détection de configuration complète: si la concaténation des ensembles P, Q
et R comporte 9 chiffres. La mise sous forme d'ensemble {op(P)}, élimine les éléments redondants lors de
la concaténation. Enfin, on calcule le cumul des quantités de
cartons et Tot. En bleu, le résultat du traitement selon la
demande d'impression: qunatité de configurations (kt),
quantité totale de cartons (Tot) et la
même valeur en notation cientifique. _________________________________ Cas
de 1 ou 2 nombres par colonne Dans la procédure, si kt
= 3, on annule la configuration en mettant t
à zéro. |
|
Listing
pour copie dans Maple Totcart := proc (A, B, C)
local T, i, kt, t: T := 1: for i to 9 do kt := 0: if evalb(i in A) then kt :=
kt+1 end if: if evalb(i in B) then kt := kt+1 end if: if evalb(i in C) then
kt := kt+1 end if: if i = 1 then if kt = 1 then t := 9 elif kt = 2 then t :=
36 elif kt = 3 then t := 84 end if: if kt <> 0 then T := T*t end if end
if: if 1 < i and i < 9 then if kt = 1 then t := 10 elif kt = 2 then t
:= 45 elif kt = 3 then t := 120 end if: if kt <> 0 then T := T*t end if
end if: if i = 9 then if kt = 1 then t := 11 elif kt = 2 then t := 55 elif kt
= 3 then t := 165 end if: if kt <> 0 then T := T*t end if end if end
do: return T end proc: L1 := [1, 2, 3, 4, 5, 6, 7, 8, 9]: L2 := [1, 2, 3, 4,
5, 6, 7, 8, 9]: L3 := [1, 2, 3, 4, 5, 6, 7, 8, 9]: with(combinat): qt := 5:
P1 := choose(L1, qt): q1 := nops(P1): P2 := choose(L2, qt): q2 := nops(P2):
P3 := choose(L3, qt): q3 := nops(P3): kt := 0: Tot := 0: for i to q1 do P :=
P1[i]: for j to q2 do Q := P2[j]: for k from 1 to q3 do R := P3[k]: if P
<> Q and P <> R and Q <> R and nops({op(P), op(Q), op(R)})
= 9 then kt := kt+1: TT := Totcart(P, Q, R): Tot := Tot+TT end if end do end
do end do: print(kt, Tot, evalf(Tot)): |
|
Voir Programmation – Index
|
|
||
|
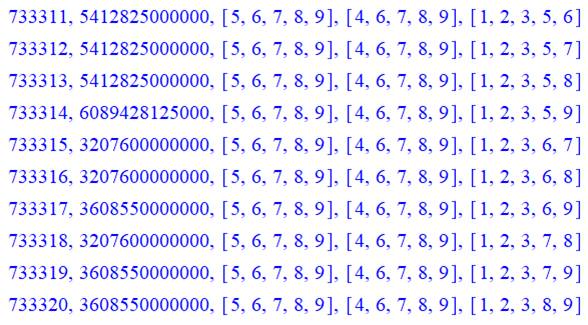
Début |
Rang, quantité de cartons pour
cette configuration, configuration (3 listes)
|
|
|
Intermédiaires |
|
|
|
Fin |
|
|
|
Records La configuration suivante produit un plus grand
nombre de cartons |
|
|
Merci à René Brocas pour
sa coopération à la réalisation de ces pages
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()