NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/05/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Jeux et énigmes
Débutants Général	DÉPLACEMENTS				Glossaire Général
INDEX Casse-têtes	Chaîne	Tranchée	Fortin	Étoile	Pair
	Croix	Chameau et bananes		Œufs qui tombent
	Verres	Grenouilles sauteuses
	Sommaire de cette page >>> Chaîne et hôtel >>> Solution >>> Explication

Chaîne et hôtel
Le client a un arrangement avec l'hôtel. Il règle chaque nuit passée avec un maillon de sa chaîne en or qui en comporte 21. Comment s'y prendre en coupant un minimum de maillons ? Le paiement est effectué très régulièrement, au jour le jour. La chaîne est bien entendu libre à chaque extrémité.

Solution

Indice

En coupant deux maillons, je peux payer le premier jour et le deuxième jour. En ayant coupé le quatrième maillon, je peux disposer d'un morceau de chaîne de trois maillons. Je le donne au caissier en lui demandant de me rendre les deux premiers. Je paie ainsi mon troisième jour. Quel maillon faut-il couper pour payer mon deuxième jour, et ainsi poursuivre astucieusement à payer mon séjour de 21 jours ?

Solution

Chaîne et hôtel - Solution
La solution consiste à couper seulement deux maillons: le 4 et le 10 Soit 2 maillons libres et 3 chaînettes de 3, 5 et 11 maillons: Une variante consiste à couper le maillon 11 au lieu du 10.

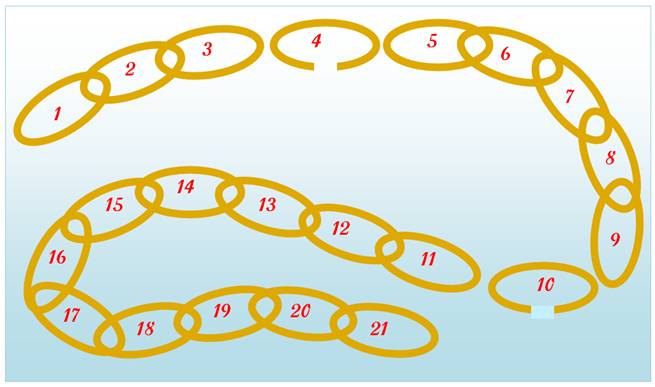
Nuit	Le client possède	L'hôtel possède
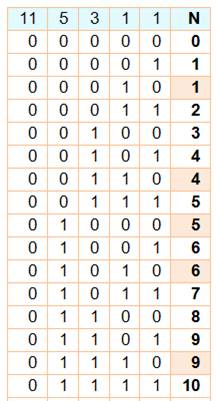
0	1 – 1 – 3 – 5 – 11
1	1 – 3 – 5 – 11	1
2	3 – 5 – 11	1 – 1
3	1 – 1 – 5 – 11	3
4	1 – 5 – 11	1 – 3
5	1 – 1 – 3 – 11	5
6	1 – 3 – 11	1 – 5
7	3 – 11	1 – 1 – 5
8	1 – 1 – 11	3 – 5
9	1 – 11	1 – 3 – 5
10	11	1 – 1 – 3 – 5
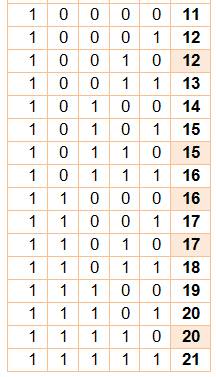
11	1 – 1 – 3 – 5	11
12	1 – 3 – 5	1 – 11
13	3 – 5	1 – 1 – 11
14	1 – 1 – 5	3 – 11
15	1 – 5	1 – 3 – 11
16	1 – 1 – 3	5 – 11
17	1 – 3	1 – 5 – 11
18	3	1 – 1 – 5 – 11
19	1 – 1	3 – 5 – 11
20	1	1 – 3 – 5 – 11
21		1 – 1 – 3 – 5 – 11

Retour

Explications

La solution ci-dessous montre un procédé qui s'apparente de près à une méthode de numération dans une base spécifique. Le tableau indique les 32 valeurs possibles. Ce système de numération n'est pas performant car il donne 10 valeurs redondantes (en marron). Quelle est la taille maximum de la chaîne avec coupure de deux maillons seulement ? C'est 23, avec coupure des maillons 4 et 11. La taille des chaînettes est: 1, 1, 3, 6 et 12, et les possibilités sont les suivantes:

Suite	Voir haut de page Chaîne et ses maillons Jeux et énigmes – Index
Voir	Partage – Énigmes classiques Partage en dix Polygone, Octogone
DicoNombre	Nombre 28
Aussi	Partage et dédommagement Partage lors d'un repas en commun Partage de Pascal
Cette page	http://villemin.gerard.free.fr/aJeux1/Deplacem/Chaine.htm