NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/10/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Jeux et énigmes
Débutants Général	DÉPLACEMENTS				Glossaire Général
INDEX Casse-Tête	Chaîne	Tranchée	Chèvre, chou et loup	Étoile
	Pair	Croix	Chameau et bananes	Fortin
	Verres		Problème de Josèphe
		Sommaire de cette page >>> Le fortin >>> Autres versions de cette énigme (texte des auteurs) >>> L'abbesse et ses religieuses >>> Le bourgeois et sa cave

Récréations mathématiques

Énigme des gardes du fortin,

Énigme de l'Abbesse, et

Énigme du bourgeois

Ces énigmes très proches se trouvent:

chez Bachet de Méziriac (1581-1638) – Problèmes plaisans et délectables;

chez Jacques Ozanam (1640-1718) – Récréations mathématiques et physiques;

et chez Euler (1707-1783).

GARDES du FORTIN
Un sergent a placé ses trente-six gardes autour du fortin, neuf gardes par côté. Il vérifie toutes les heures que cette disposition est bien respectée: il y a bien 9 gardes par face du fortin. Mais les gardes sont malins et resquillent …Voyons comment heure par heure

Note: Je n'ai pas retrouvé de référence accordant la paternité de cette énigme à Euler.

HEURE par HEURE

20 heures

0	9	0
9	F	9
0	9	0

9 gardes par côté; total 4 x 9 = 36

22 heures

1	7	1
7	F	7
1	7	1

9 gardes par côté; total 4 x 7 + 4 = 32

24 heures

2	5	2
5	F	5
2	5	2

9 gardes par côté; total 4 x 5 + 4 x 2 = 28

02 heures

3	3	3
3	F	3
3	3	3

9 gardes par côté; total 8 x 3 = 24

04 heures

4	1	4
1	F	1
4	1	4

9 gardes par côté; total 4 x 4 + 4 = 20

21 heures

0	8	1
8	F	8
1	8	0

9 gardes par côté; total 4 x 8 + 2 = 34

23 heures

2	6	1
6	F	6
1	6	2

9 gardes par côté; total 4 x 6 + 4 + 2 = 30

01 heure

3	4	2
4	F	4
2	4	3

9 gardes par côté; total 4 x 4 + 6 + 4 = 26

03 heures

4	2	3
2	F	2
3	2	4

9 gardes par côté; total 4 x 2 + 8 + 6 = 22

05 heures

4	0	5
0	F	0
5	0	4

9 gardes par côté; total 8 + 10 = 18

Bilan

En ne comptant que la quantité de gardes par côté, le sergent ne s'est pas aperçut que deux gardes disparaissaient toutes les heures!

Au petit matin, seuls 18 gardes étaient de faction, et (36 – 18 =) 18 étaient en train de jouer tranquillement aux cartes.

Autres versions – Textes exacts des auteurs
Bachet	Ozanam
Un bon bourgeois fit faire dans sa cave un casier de neuf cases disposées en carré; la case du milieu était destinée à recevoir les bouteilles vides provenant de la consommation de soixante bouteilles pleines, qu'il disposa dans les huit autres cases en mettant six bouteilles dans chaque case des angles et neuf dans chacune des autres cases. Son domestique enleva d'abord quatre bouteilles qu'il vendit, et il disposa les bouteilles restantes de manière qu'il y en eût toujours vingt- et-une sur chaque côté du carré. Le maître, trompé par cette disposition, pensa que son domestique n'avait fait qu'une transposition de bouteilles, et qu'il y en avait toujours le même nombre. Le domestique profita de la simplicité de son maître pour enlever de nouveau quatre bouteilles, et ainsi de suite jusqu'à ce qu'il ne fût plus possible d'en enlever quatre sans que le nombre vingt-et-un cessât de se trouver sur chaque côté du carré. On demande comment il s'y prit à chaque fois, et de combien de bouteilles il fit tort à son maître. Solution	Une abbesse aveugle vérifiant les religieuses qui sont dispersées également dans huit cellules construites aux quatre angles d’un carré, et au milieu de chaque côté, trouve partout un nombre égal de personnes dans chaque rang qui est composé de trois cellules: et en les vérifiant une seconde fois, elle trouve dans chaque rang le même nombre de personnes quoiqu’il soit entré quatre hommes: et en les vérifiant une troisième fois, elle trouve encore dans chaque rang le même nombre de personnes quoique les quatre hommes soient sortis, chacun avec une religieuse; on demande comment cela se peut et se doit se faire. Solution

L'abbesse et ses religieuses (Ozanam)
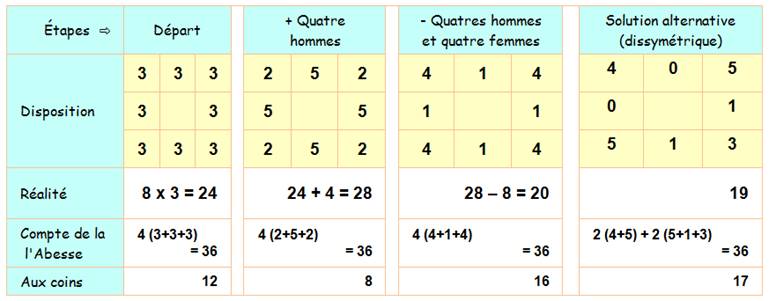
Exemple avec trois religieuses par cellules, trente-six au total. En fait l'abbesse ne fait pas le total; elle compte neuf religieuses sur chaque côté. Remarquez l'attitude naïve de l'abbesse qui compte systématiquement deux fois les religieuses des angles. La réalité est bien égale au compte de l'abbesse diminué des présentes aux coins. Exemple au départ: 24 = 36 – 12.

La cave du bourgeois (Bachet)
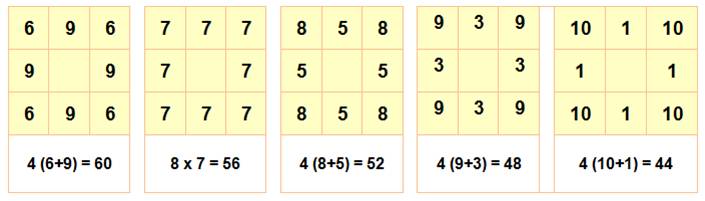
Le domestique réussit à subtiliser quatre bouteilles à chaque fois. Il pourra répéter l'opération à la barbe du bourgeois quatre fois. Le propriétaire compte toujours vingt-et-une bouteille par rangée; pourtant le total de bouteille diminue. Finalement, le domestique aura subtiliser 16 bouteilles (66 – 44) .

Suite	Jeux et énigmes – Index Sentinelle dans sa guérite en un seul trait Remettre les verres dans le même sens Problème de Josèphe
Voir	Énigmes des œufs qui tombent du centième étage Partage – Énigmes classiques Partage en dix Polygone, Octogone
DicoNombre	Nombre 7 Nombre 33 Nombre 36 Nombre 37
Aussi	Partage et dédommagement Partage lors d'un repas en commun Partage de Pascal
Cette page	http://villemin.gerard.free.fr/aJeux1/Deplacem/Fortin.htm