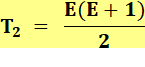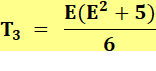|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
ŒUFS qui TOMBENT du 100e ÉTAGE Énigme des boules de cristal Énigme casse-tête qui
demande depuis quel étage un œuf qui tombe se casse sûrement. Deux œufs sont
proposés pour faire les tests. La question: combien d'essais sont nécessaires
au mieux? Problème
d'optimisation de déplacements plutôt
que de partage. |
Anglais: Dropping eggs puzzle, 2 Eggs-100 Floors puzzle, The
Two Egg Problem
|
Nous
disposons de deux œufs absolument
identiques.
Le problème
est de savoir à partir de quel étage cela se passe. Dit-autrement, lâchés des
étages inférieurs, ils ne se casseront pas. Combien
d'essais, au maximum, sont nécessaires pour connaitre la réponse? La réponse
optimale est 14. Comment trouver ce résultat? Note: avec un seul
œuf, il suffit de faire tous les étages successifs à partir du premier et de
s'arrêter lorsque l'œuf casse. Au pire, il faut 100 essais. L'énigme proposée
met deux œufs à votre disposition et il s'agit de minimiser la quantité des
essais. Quelle est la meilleure stratégie? Pour les puristes: si les œufs se
cassent à partir d'un étage donné, ils se cassent pour tous les étages
supérieurs. S'ils ne cassent pas, ils ne cassent pas pour les étages
inférieurs. Ils peuvent se casser dès le premier étage ou alors, résister
jusqu'au dernier étage. Tout dépend de la nature des œufs. |
|
Ce magicien mesure 1,73 mètre et il tient
un œuf frais dans sa main. L'œuf chute sur près de deux mètres sans se
casser. Comment fait-il ? Réponse: il est monté sur la table! |
|
|
||
|
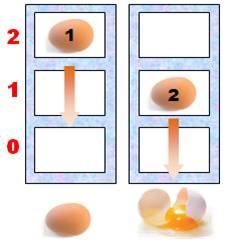
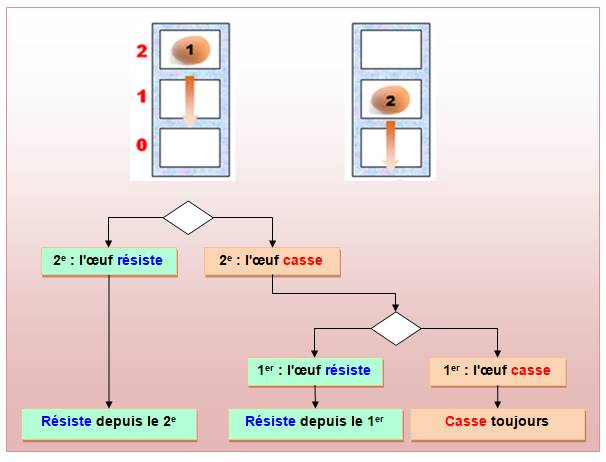
Deux étages Évidemment,
l'œuf peut se casser au premier essai, mais au pire, il faudra effectuer 2
essais. Bilan: avec un
bâtiment de deux étages (B = 2), il faut au maximum deux essais (E = 2). |
Avec 2
étages, 2 essais suffisent |
|
Algorithme
du test avec deux étages
Merci à Frédéric Smietanski pour sa contribution
|
|
||
|
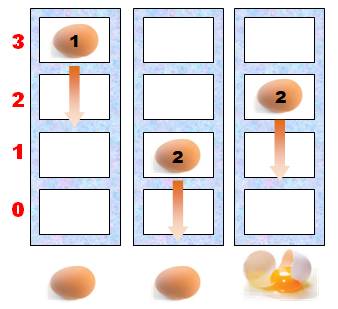
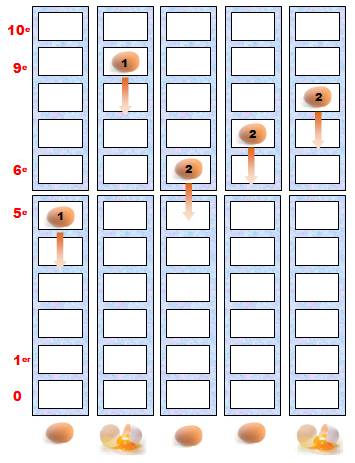
Idée En fait,
le bâtiment comporte beaucoup d'étages, mais nous allons tester d'abord le bloc
des cinq premiers étages. Cinq étages Le cas critique serait que les œufs se cassent à
partir du 4e étage. Avec le 1er œuf, on teste la 5eétage.
Cas critique, il se casse. On doit alors poursuivre les essais en testant
l'étage le plus bas et monter progressivement jusqu'au 4e. Dans le cas le plus extrême, il faut 5 tests. Notez que si, in fine, l'œuf ne se casse pas, c'est
que ces œufs sont résistants au 5 étages. |
5 étages, cas critique
Avec un
bloc de 5 étages, il faut 5 essais |
|
|
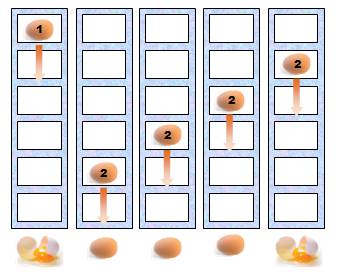
Idée Si avec
un essai sur 5 étages le premier œuf ne se casse pas, c'est que l'étage
cassant est plus haut. Le deuxième
œuf est disponible pour tester les étages supérieurs. Contrainte:
ne pas utiliser plus d'essais que les 5 précédents. Oui, mais il ne reste
plus que 4 essais possibles. Donc, l'œuf lâché du 5e étage résiste:
Bilan: avec cinq
essais imposés, il est possible de tester un bâtiment de 9 étages (pas 10). Suite: si l'œuf n°1 ne casse
pas au deuxième essai à partir du 9e étage, c'est que l'étage
cassant est au-dessus. Les essais se poursuivent … |
9 étages
Avec 5 essais, on peut tester un bloc de 5 étages puis un bloc de 4
étages |
|
|
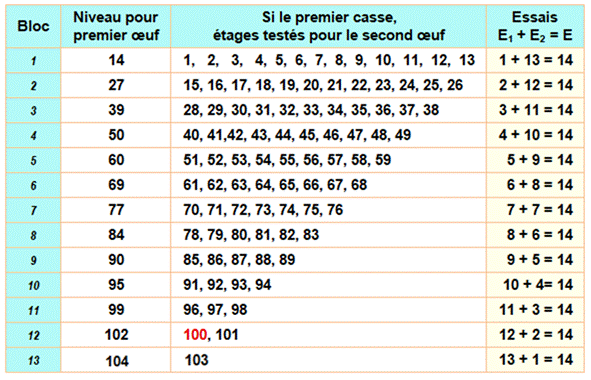
Règle des blocs Ce
raisonnement montre que chaque fois que le premier œuf résiste, on peut
monter d'un bloc d'étages, mais avec un étage de moins que dans le bloc
précédent. Le tableau montre que, pour 5 essais, on peut
aller jusqu'à 5 blocs conduisant à 15 étages. Remarque: la quantité
d'étages dans le bloc de départ détermine la quantité
d'essais: B = E. |
15 étages
Avec 5 essais, on peut tester 5
blocs totalisant
15 étages, et 15 = 1 +
2 + 3 + 4 + 5. |
|
|
|
|||||
|
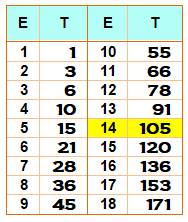
Conclusion de nos observations Avec un
étage de moins à chaque bloc supérieur, la totalité (T) des étages atteints
est la somme
des entiers jusqu'à E. Avec E = 10 essais, on commence à tester un bloc
de B = 10 étages, ce qui conduit à pouvoir tester un bâtiment qui compte
jusqu'à T = 55 étages. Nous approchons des 100 demandés. |
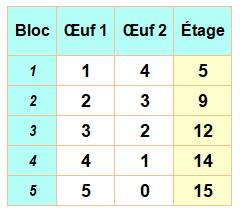
Avec 5 essais, donc un premier bloc
de 5 étages B = E = 5 T = 1 + 2 + 3 + 4 + 5 = ½ x 5 x 6 = 15 Il est possible de tester 15 étages Avec 10 essais, donc un premier
bloc de 10 étages B = E = 10 T = 1 + 2 + 3 + … + 10 = ½ x 10 x 11 = 55 Il est possible de tester 55 étages |
||||
|
Formulation pour k étages Il s'agit
de trouver une somme d'entiers qui atteint T = 100. |
Pour T = 100 étages 200 = E (E + 1) |
||||
|
Solution: deux possibilités En fait, avec 14 essais, il est possible de tester 105 étages. Avec 3 œufs, il faudrait seulement 9 essais |
Tableau
de la somme T
|
Résolution de l'équation E² + E – 200 = 0 Équation du second
degré dont les racines sont: 13,65… et -14, 65 … On retient la racine positive et son arrondi supérieur soit: 14 essais. |
|||
|
Avec 3 œufs Il faudrait seulement 9 essais pour les 100 étages. |
|
||||
Bilan: tableau des tests réalisés (au pire)
pour 104 étages
|
|
|
|
Two Egg problem:
|
|
Voir Anglais – Le bagage minimum
![]()
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()