|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mono: une bille
est plus lourde (ou plus légère) Ambi: une
bille est plus lourde ou plus légère sans
que nous le sachions a priori |
![]()
|
Énigme de la pesée des QUATRE BILLES ou BALLES, BOULES, PIÈCES Une petite énigme simple
avec d'aborder l'énigme réputée impossible des douze
billes. Avant la lecture de cette page vous pouvez commencer par l'énigme
encore plus simple des neuf billes. La résolution n'est pas très
compliquée, mais source d'observations utiles pour la résolution d'énigmes
plus complexes. Nous
découvrirons qu'avec quatre billes:
|
|
|
||
|
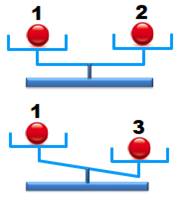
Avec
trois billes dont l'une est plus lourde, nous
savons détecter la bille fautive. |
|
|
|
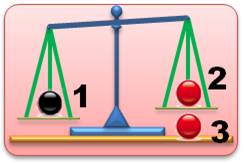
Avec
quatre billes dont l'une est plus lourde que les trois autres, une seule
pesée ne suffit pas, sauf coup de chance. Avec deux
pesées, il y alors plusieurs possibilités. La méthode classique consiste à comparer les
billes par groupes puis individuellement. C'est la méthode par dichotomie ou focalisation
progressive sur la bille fautive. Ici, c'est la bille
1 qui est la plus lourde. |
Méthode classique
|
|
|
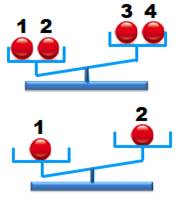
La méthode rapide consiste à comparer les
biles deux à deux. Avec un peu de chance la seconde pesée n'est pas
nécessaire. Ici, c'est la
bille 3 qui est la plus lourde. |
Méthode rapide
|
|
|
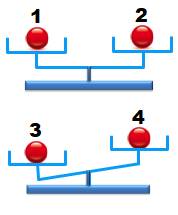
La méthode astucieuse consiste à se servir des
données acquises pour poursuivre les investigations. Elle sera mise à profit
pour les cas concernant un grand nombre de billes. Ici, la première
pesée indique que les billes 1 et 2 sont standard. La bille 1 est réutilisée
pour la comparer à 3. Ici, la bille 3 se trouve la plus lourde. En cas d'équilibre
en seconde pesée, la bille 4 est la plus lourde. |
Méthode astucieuse
|
|
Je réfléchis …
|
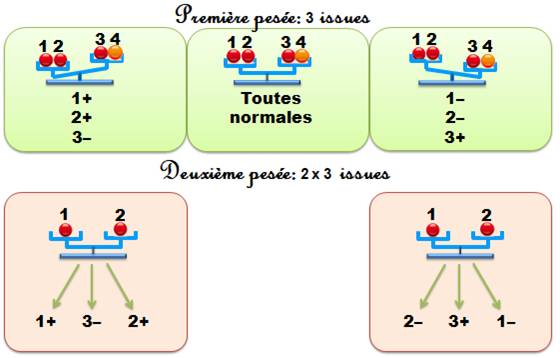
Avec la première pesée, il y a trois
issues (+, = , –) Pour chacune de ces pesée, il y a trois issues (+, = , –) Pour les deux pesées, il a donc neuf issues. Largement plus qu'il n'en faut pour trouver la
plus lourde parmi quatre billes. Et si la bille fautive était plus ou plus légère sans
qu'on le sache, il y aurait huit
conclusions possibles. Huit possibilités pour neuf issues de pesées ça
devrait marcher …sauf contrainte inattendue ! |
![]()
|
|
||
|
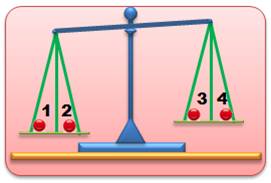
Vous
disposez de quatre billes absolument identiques visuellement. Une parmi
les quatre est plus lourde ou plus légère (ambivalence), mais nous ne savons
pas. En deux
pesées sur une balance à deux plateaux (type Roberval
ou trébuchet), trouvez l'intrus et sa nature. |
Exemple de pesée
Mais est-ce le
bon départ ? Non ! |
|
|
|
||||
|
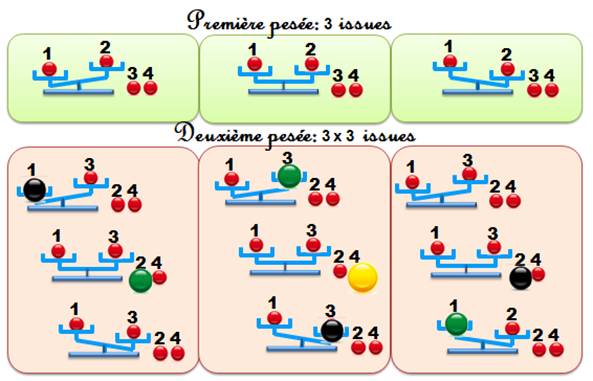
Le tableau des issues des deux pesées se présente
de cette manière. Voyons ce que l'on peut en tirer. Sur le dessin: Bille noire: lourde Bille verte: légère Bille jaune: fautive |
|
|||
|
Bille 1 lourde |
P1: le plateau gauche descend |
P2: le plateau gauche descend |
+ + |
|
|
Bille 1 légère |
P1: le plateau gauche monte |
P2: le plateau gauche monte |
– – |
|
|
Bille 2 lourde |
P1: le plateau gauche monte |
P2: plateaux en équilibre |
– 0 |
|
|
Bille 2 légère |
P1: le plateau gauche monte |
P2: plateaux en équilibre |
+ 0 |
|
|
Bille 3 lourde |
P1: plateaux en équilibre |
P2: le plateau gauche monte |
0 – |
|
|
Bille 3 légère |
P1: plateaux en équilibre |
P2: le plateau gauche descend |
0 + |
|
|
Bille 4 indéterminée |
P1: plateaux en équilibre |
P2: plateaux en équilibre |
0 0 |
|
Remarquez
|
Les
conclusions "plus lourde" ou "plus légère" pour une bille
sont opposées en signe: "plus" pour l'une devient "moins"
pour l'autre. Remarque
qui sera utile pour les énigmes plus complexes. |
|
|
||
|
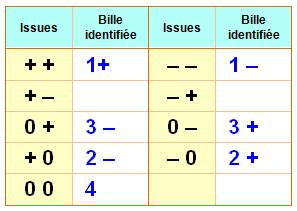
Le tableau des issues de pesées Ce
tableau montre un résumé de la situation. Le signe + indique que le plateau
gauche descend et le signe – qu'il monte; le 0 indique l'équilibre. Associé
aux billes, le signe + indique plus
lourd et le signe – moins lourd. Observations
|
Notez que: une bille peut
être ++ ou – – Elle peut être associée à un 0 neutre. Mais, jamais associée à deux signes contraires: elle ne peut pas
être à la fois lourde et légère. |
|
|
|
||
|
Parmi les quatre billes
Avec deux pesées, il est possible de les
discriminer comme indiqué sur l'illustration. |
En bas des cases vertes, on note la conclusion de
la pesée. En bas des cases roses, on indique la conclusion
de la pesée selon le mouvement des plateaux. |
|
|
Cas de quatre billes + une |
|
|
|
Parmi les cinq billes
Avec deux pesées, il est possible de les
discriminer comme indiqué sur l'illustration. |
La méthode est rigoureusement identique à celle
exposées ci-dessus pour 3 billes + 1,
avec les différences suivantes:
|
|
![]()
|
Retour |
|
|
|
|
|
Voir |
|
|
|
|
|
Sites |
Voir
liste |
|
Cette
page |
![]()