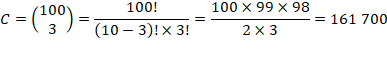|
|||||||||||||||||||||||||||||
![]()
|
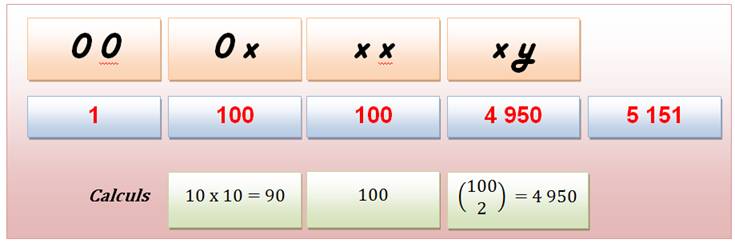
Étude 67 – Combinaisons 100 Sur cette page, étape 3, nous allons compter les
combinaisons avec des nombres de 1 à 100. Quelles sont toutes les additions
possibles avec deux, trois ou quatre termes, avec les nombres de 1 à 100,
quelle que soit la somme. |
Voir Nombre
67
|
|
|
|
Il en reste 5 050 en
excluant les termes nuls. |
|
|
|
||
|
|
Rxxy
= 100 x 100 = 10 000 S = 161 700 + 10 000 =
171 700 |
|
|
|
|
|
|
|
|
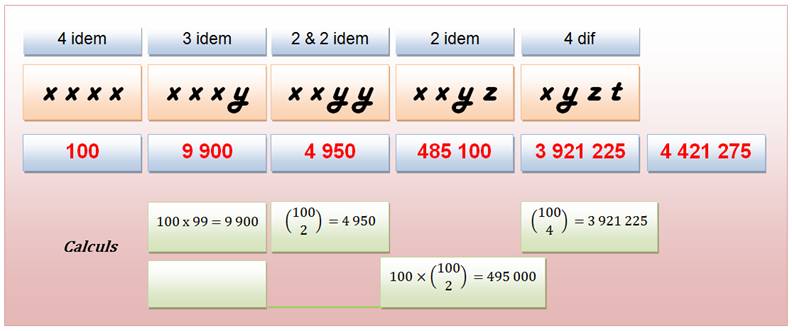
Quantité de sommes
distinctes avec n termes de 1 à 100: n = 1 n = 2 n = 3 n = 4 Total: 4 598 026 |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()