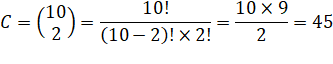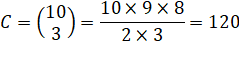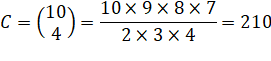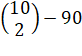NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/02/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	PARTITIONS
Débutants Addition	Étude avec 67			Glossaire Addition
INDEX Partitions Dénombrement Calculs	Combinaisons 10	Somme 7	Combinaisons 100	Somme 67
		Sommaire de cette page >>> Ce que l'on cherche >>> Addition avec deux termes de 1 à 10 >>> Addition avec trois termes de 1 à 10 >>> Addition avec quatre termes de 1 à 10 >>> Bilan

Étude 67 – Combinaisons 10

Études en quatre étapes des partitions avec comme exemple le nombre 67. Dénombrement des sommes de un à quatre termes avec des nombres de 1 à 100.

Sur cette page, étape 1, nous allons simplement compter les sommes distinctes quel que soit le résultat. Les trois premières étapes ne sont pas strictement nécessaires. Elles permettent de se familiariser avec le problème et, surtout, de pratiquer des exercices de dénombrement.

Compter les sommes avec quatre termes distincts (1 + 2 + 3 + 4, 1 + 2 + 3 + 5 …) est un exercice classique de calculs de combinaisons. Le dénombrement est plus compliqué pour les sommes avec termes doublonnés comme 1 + 1 + 2 + 3, 1 + 1 + 1 + 2 …)

Voir Nombre 67

Ce que l'on cherche
Au départ, il s'agit de trouver toutes les partitions à quatre nombres de 67. Quelles sont toutes les possibilités d'obtenir 67 en ajoutant quatre nombres compris entre 1 et 100? Un logiciel de calcul donne immédiatement la solution. D'accord mais comment calculer ce résultat? Démarrons doucement avec deux termes jusqu'à 10.	1 + 2 + 3 + 61 = 67 1 + 22 + 22 + 22 = 67 etc. Il y a 2 586 partitions dont 2 178 sans 0 (ou quatre termes non-nuls).

Addition avec deux termes de 1 à 10
Commençons par compter toutes les possibilités d'additionner deux nombres de 1 à 10. Comme 1 + 1, 1 + 2, 1+ 3, …2 + 1 … La table de toutes les possibilités montre que: il ya 10 x 10 = 100 possibilités, certaines sont identiques pour l'addition, comme 1 + 2 = 3 et 2 + 1 = 3, d'autres affichent des termes répétés comme1 + 1 ou 2 + 2. Illustration: les 100 arrangements avec: en bleu les combinaisons de deux nombres distincts; en jaune clair, à nouveau, toutes les combinaisons de deux nombres distincts, symétrique du précédent; et en jaune foncé, les sommes à deux chiffres identiques.
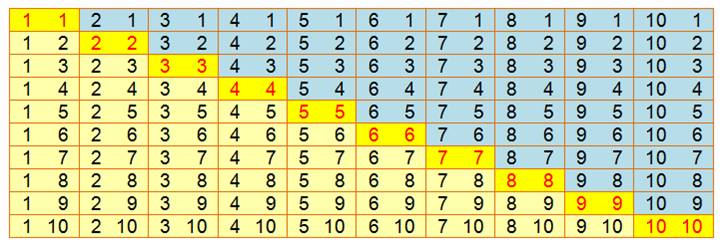
Quantité d'arrangements de deux fois dix nombres (tout le tableau). Quantité de combinaisons (zone bleu ou zone jaune claire). Quantité de somme à chiffres répétés (zone en jaune foncé). Quantité de sommes distinctes avec deux nombres de 1 à 10 (zone jaune foncé et jaune clair).	A = 10^2 = 100 R = 10 S = 100 – 45 = 45 + 10 = 55

Addition avec trois termes de 1 à 10
Il s'agit de compter toutes les possibilités d'additionner trois nombres de 1 à 10. Comme 1 + 1+1, 1 + 1 + 2, 1+ 1 + 3, …2 + 2 + 3 … Illustration: les 1000 arrangements avec en jaune, les sommes uniques à trois termes; en marron, les sommes identiques à celles dans la colonne correspondante, les termes étant commutés; en bleu, toutes les sommes éliminées du fait de leur existence dans les cellules déjà e jaune; et en chiffres rouges, les sommes avec répétitions de termes.
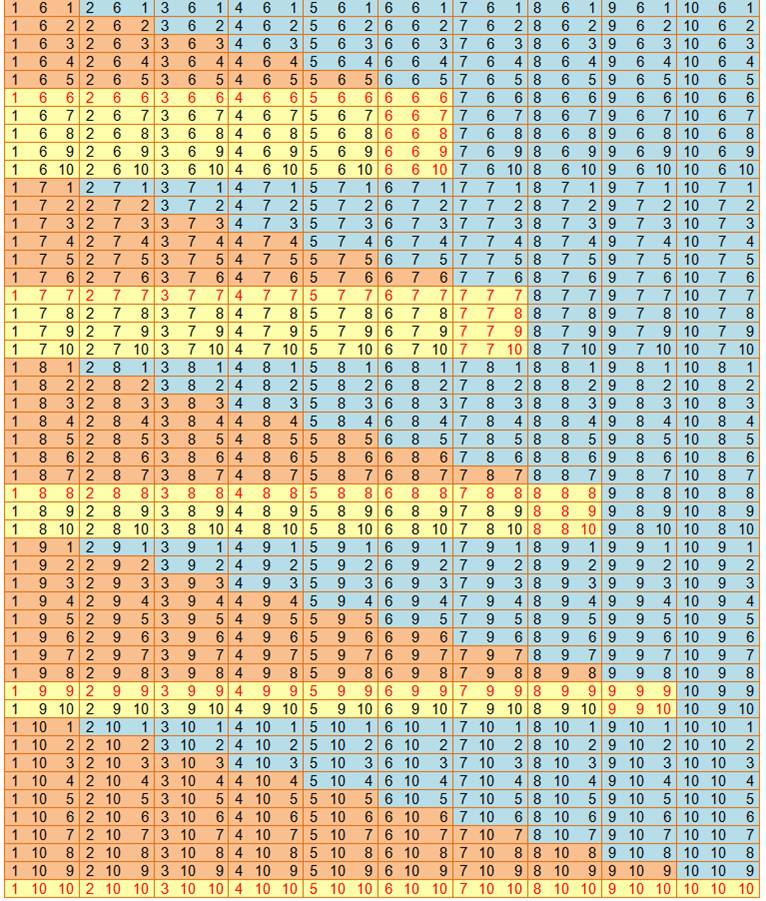
Quantité d'arrangements de trois fois dix nombres (tout le tableau). Quantité de combinaisons (choix de trois nombres distincts parmi 10). Quantité de sommes avec termes répétés (chiffres en rouge). Remarquez qu'ils sont disposés en une équerre de 10 sommes. Quantité de sommes distinctes de trois termes avec des nombres de 1 à 10.	A = 10^3 = 1000 R = 10 x 10 S = 120 + 100 = 220

Addition avec quatre termes de 1 à 10
Avec quatre termes, les configurations se multiplient: quatre termes tous identiques ou tous différents; quatre termes égaux deux à deux; trois termes identiques, différents du quatrième; et deux termes identiques et les deux autres différents. Voici le tableau récapitulatif avec le décompte des possibilités:
Quantité d'arrangements de trois fois dix nombres. Quantité de combinaisons (choix de quatre nombres distincts parmi 10). Quantité de sommes avec termes répétés: de type xxxx (1111, 2222 … 10 fois) de type xxxy (1112, 1113 … 10 fois 9) de type xxyy (tirage de deux blocs distincts parmi 10) de type xxyz (tirage de deux termes distincts parmi 10 et retrait des doublons en xxy)) Quantité de sommes distinctes de quatre termes avec des nombres de 1 à 10.	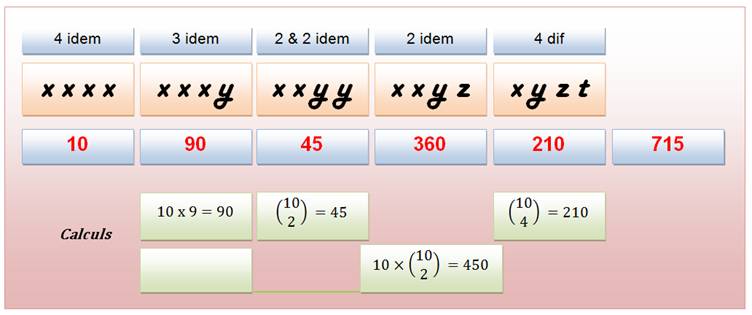A = 10^4 = 10 000 Rxxxx = 10 Rxxxy = 10 x 9 = 90 Rxxyy = = 45 Rxxyz =10 x = 450 – 90 = 360 S =210 + 10 + 90 + 45+360 = 715

Bilan

Quantité de sommes distinctes avec n termes de 1 à 10:

n = 1 1

n = 2 55

n = 3 220

n = 4 715

Total: 991

Suite	Étape 2 – Somme égale à 7
Voir	Conjecture d'Euler
Cette page	http://villemin.gerard.free.fr/aMaths/Partition/N67C10.htm