|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
COURBES k-sécantes Dénombrement Nous
avons identifié tous les cas de courbes qui se croisent deux fois. Nous allons
tenter de formaliser l'approche avec l'espoir d'une généralisation à k
intersections. Exemples de courbes k-sécantes
|
|
On
ne peut plus simple, voire évident, mais extrêmement difficile à démontrer. Ligne de Jordan: une ligne continue et
fermée dans le plan, sans croisement. Théorème de Jordan: une ligne de Jordan
découpe le plan en deux Critère du chemin: un chemin qui part de
l'intérieur et arrive à l'extérieur coupe la courbe un nombre impair de fois.
Sur l'illustration, le point rouge est à l'extérieur car le chemin vert coupe
deux fois (pair) la courbe. |
Voir Théorème
de Jordan
|
|
||
|
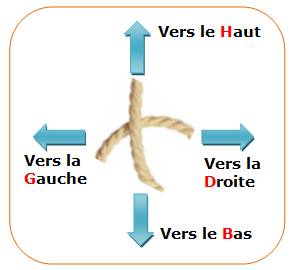
Une
courbe k-sécante est une ligne courbe de
l'espace qui, projetée sur un plan, se croise k fois. Elle crée
k intersection en croix, comme une ficelle
lâchée sur le sol. L'intersection représentée par une croix droite
pointe dans quatre directions symbolisée par les lettres G, D, H et B. |
Intersection – Orientations
|
|
|
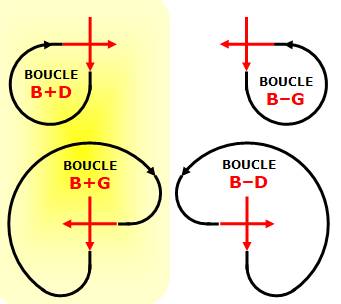
Une
courbe se croisant une fois est définie par la direction d'entrée et celle de
sortie, plus le sens de formation de la boucle. On commence la boucle par un mouvement vers le
bas (B). Les autres départs s'en déduisent par simple rotation. Ensuite la boucle part dans le sens horaire (+)
ou antihoraire (-) pour aller rattraper la direction transverse dans un sens
(droite) ou dans l'autre (gauche). Soit quatre possibilités. En fait, posée sur une table en verre, les
boucles montrées sur la gauche de l'illustration sont les mêmes que celles de
droite. Elles sont superposables et identiques en topologie (symétrique
par rapport à une droite). On conserve comme modèle de base les deux figures
de gauche en privilégiant le sens horaire. |
Les quatre boucles élémentaires dont deux sont à
retenir
Une courbe avec une intersection crée une boucle
qui définit un intérieur et un extérieur. Ici, les points de départ et arrivée sont tous
deux intérieurs ou extérieurs. |
|
|
|
||
|
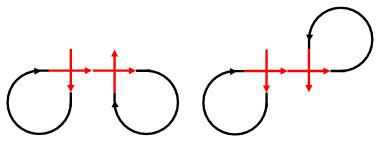
Cas de la
boucle élémentaire du haut à laquelle on ajoute la même boucle en sortie. Deux cas sont possibles: la deuxième boucle est
horaire ou antihoraire. |
B+D = D+H &
B+D = D–B |
|
|
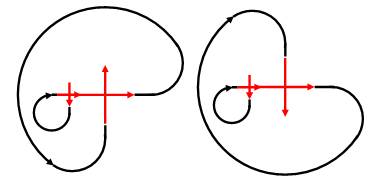
Cas de la
boucle élémentaire du haut à laquelle on ajoute la boucle du bas en sortie. Deux cas sont possibles: la deuxième boucle est
horaire ou antihoraire. |
B+D = D–H &
B+D = D+B |
|
EN COURS
…
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Rien sur le sujet de cette
page, voir néanmoins:
|
|
Cette page |
![]()