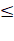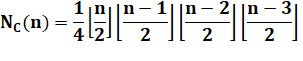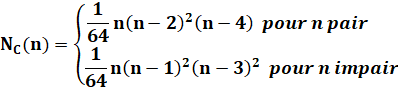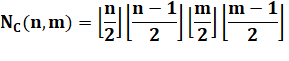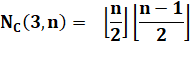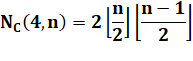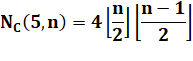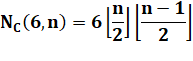|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombre de CROISEMENTS des graphes Graph Crossing numbers En topologie
et en théorie
des graphes, on connait la théorie des nœuds. On
connait aussi cette célèbre énigme des trois
maisons à alimenter en eau, gaz et électricité sans croisement de
réseaux. Problème généralisé sous le nom de la brique de Turan (Turan brick
factory problem). Ici, on
s'intéresse aux graphes qui présentent des croisements inévitables. Pour un
graphe donné, quelle est la quantité d'intersections inévitables (Anglais: graph
crossing number). |
Vocabulaire
|
Sommet
ou nœuds du graphe (one vertex or vertice, several vertices). Arêtes
ou lien (edge). |
|
|
||
|
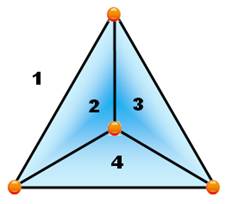
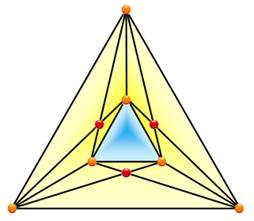
Quatre points Quatre
points quelconques non alignés sont reliés entre eux. Aucun
croisement. Les
arêtes découpent le plan en quatre régions numérotées de 1 à 4. Et si un cinquième point ? Un cinquième point ferait partie d'une des quatre régions (T):
triangle ou extérieur à un triangle (pseudo-triangle). À ce titre, il est
facile de le relier aux trois sommets de T. Par contre, pour relier le
quatrième sommet, le segment devra traverser une frontière de T en créant
nécessairement un croisement. |
NC(K4) = 0 |
|
|
|
||
|
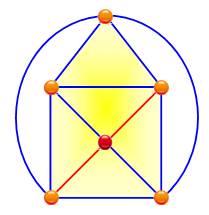
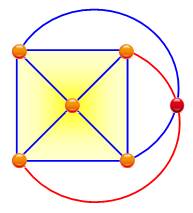
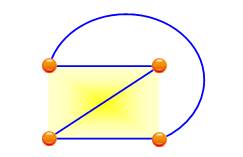
Avec cinq
sommets disposés en pentagone ou en carré centré (le cinquième point à
l'intérieur ou à l'extérieur du quadrilatère formé par les quatre autres), il
est impossible de les relier tous entre eux sans créer une intersection, un
croisement. Le nombre
de croisements minimum pour le graphe K5 est 1. Définition: le nombre de croisements d'un graphe est la
quantité minimale de croisements entre arêtes pour tous les dessins possibles
du graphe dans le plan. Un graphe
planaire est un graphe dont le nombre de croisements est nul. Le nombre
de croisements est alors une indication du degré d'éloignement du graphe
planaire. En imposant des arêtes droites, on définit le nombre de croisements rectilignes Type de problème: calculer le nombre de croisements d'un graphe
est un problème compliqué. C'est un problème
NP-Complet. |
NC(K5) = 1 (en rouge) |
|
|
Si le
graphe est planaire, il représente un polyèdre
auquel on peut appliquer la relation
d'Euler: F + S = A + 2 => F
+ 5 = 10 + 2 => F = 7. Ces 7 faces
mettent en jeu au moins 7 x 3 = 21 arêtes. Chacune étant comptée deux
fois, il y a au moins 10,5 arêtes dans le polyèdre. Or, notre vrai graphe
n'en compte que 10. Incompatible. Le graphe K5 ne peut pas être planaire. |
||
|
|
||
|
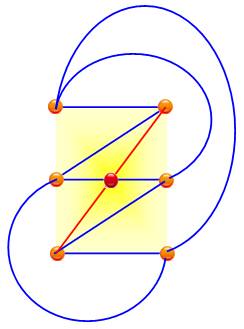
Démonstration 1 – NC (6) = 3 Supposons que le graphe ne présente que deux
croisements. Ceux-ci impliqueraient quatre sommets. Comme K6 en a six, pour deux d'entre eux, il y a formation
d'une configuration en V (ici, dessin du bas, en bleu et en vert). Supposons que l'on retire un de ces deux sommets.
Non seulement on retire un sommet, mais avec lui les deux croisements. Ce qui
voudrait dire que le nouveau graphe K5 serait planaire. Or, on sait que K5 ne
l'est pas. Contradiction. K6 n'est pas planaire et comporte
plus de deux croisements. La figure de droite montre qu'il est possible de
dessiner le graphe avec trois croisements pas plus. Démonstration 2 K6 complet => 6 sommets et 15 arêtes Supposons deux croisements, en retirant deux
arêtes, on obtient un graphe planaire: 6 sommets et 13 arêtes. Or, dans un graphe planaire:
13 |
Graphe K6
NC(K6) = 3 (en rouge) Deux croisements dans K6
|
|
|
|
||||
|
Graphe planaire pour un graphe de n sommets et a arêtes Voir Relation
d'Euler et graphes planaires |
a |
|||
|
Inégalité pour le nombre de
croisements pour un graphe de n sommets et a arêtes Exemple Avec 10 sommets, le graphe complet
compte ½ 9 x 10 = 45 arêtes. |
NC(n) NC(6) La valeur exacte est 60 |
|||
|
Conjecture de Hill
(1958, prouvée par Guy (1972) jusqu'à 10 et étendue à 12 par Pan et Richter
(2007). Elle
concerne les graphes
complets (tous les sommets sont reliés entre eux) à n sommets. |
ou encore
|
|||
|
Valeurs |
Valeurs prouvées
Suite jusqu'à n = 25 (conjecture): 225, 315, 441, 588, 784, 1008,
1296, 1620, 2025, 2475, 3025,
3630, 4356 … Par exemple: K(13) = {217, 219, 221, 223
ou 225} |
|||
|
|
||
|
Définitions Un graphe
biparti (n, m) représente la distribution de n points vers m points. Cas typique
des réseaux de distribution. Il est complet
si toutes les liaisons possibles sont réalisées. En
l'occurrence on cherche à minimiser les croisements. Formule La
conjecture de Zarnkiewicz (1954), indique que:
Elle est
vérifiée jusqu'à K(7,7) et au-delà elle surestime le nombre de croisements. En 1993,
Woodall prouve m On
connait aussi:
Valeurs (exemple K(4,3) = 2)
|
Graphe K(2, 2)
NC(K2,2) = 0 Graphe K(3, 3)
NC(K3,3) = 1 |
|
|
Démonstration pour K(3, 3) non
planaire (Semblable à celle de K5) Formule
d'Euler pour le polyèdre représentatif: F + S = A + 2 => F + 6 = 9 + 2 => F = 5. Chaque
face n'est pas triangle, sinon il y aurait des arêtes entre points n ou
points m. Quantité
minimale d'arêtes: 5 x 4 / 2 = 10.
Impossible pour le graphe K(3, 3) qui n'a que 9 arêtes. Le graphe n'est pas
planaire. |
||
|
|
||
|
The crossing number of a graph is the least
possible number of edge crossings of a plane drawing of the graph. A crossing means a point that is not a
vertex where edges meet. The drawing of a graph is made so that no
three edges cross at a single point. The complete bipartite graph K(m,n) is the graph connecting a set of m
vertices to a set of n vertices, with every eligible pair of vertices joined
by an edge. |
Le nombre de croisements d'un graphe est la quantité minimale
d'intersections d'arêtes sur le dessin d'un graphe. Une intersection est un point de croisement des
arêtes qui n'est pas un sommet. Le dessin du graphe est réalisé de sorte que
trois arêtes ne soient pas concourantes. Un graphe biparti complet K(m, n) est le graphe
reliant un jeu de m sommets à un jeu de n sommets tel que toute paire
admissible de sommets forme une arête. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()