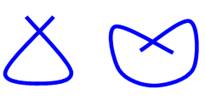|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CROISEMENTS de COURBES Dénombrement En topologie
et en théorie
des graphes, on connait le cas des nœuds; on
connait aussi le cas du décompte des croisements
minimums dans un graphe avec le cas particulier bien connu des trois
maisons à alimenter (Anglais: graph crossing number and
Turan brick factory problem). La théorie sur ces sujets se développe, mais
elle est loin d'être finalisée. Ici, on
s'intéresse aux courbes qui se croisent une fois, deux fois, k fois et à la
quantité de motifs possibles dans chaque cas. Pour une courbe, combien
y-a-t-il de façons de se croiser deux fois ? Réponse 15. Exemples avec les lettres
majuscules cursives: 0 croisement pour la lettre
O; 1 pour C et; 2 pour E, H, J et L.
|
Merci à Gilbert Chovin pour
cette idée de page à propos de ce qu'il appelle les cheminements finis sécants et bisécants
|
|
||
|
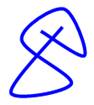
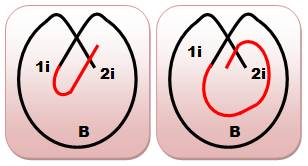
Une
courbe sur un plan. Disons une ficelle posée sur une table pour imager la
situation. Deux cas
de croisement sont possibles selon que les extrémités sont:
Le cas
d'une extrémité à l'intérieur et l'autre à l'extérieur ne forme pas un
croisement mais un simple point de tangence. |
Deux croissements autorisés et un exclu
|
|
![]()
Passage
à deux croisements (X2) ou bisécants
|
Pour obtenir un second croisement, il faut prolonger la
courbe par l'une des deux extrémités et
cela pour les deux cas de croisement unique:
2cas. Le croisement peut se produire soit en croisant la
boucle soit en croisant l'un des deux brins
d'extrémité. En fait, partir du point 1 ou du point 2 revient au même par
effet de symétrie (réflexion dans un
miroir. Restent 6 cas à examiner: 2 cas (boucle et une extrémité). Partant d'une extrémité, on peut prolonger en partant
vers la droite (sens horaire) ou vers la
gauche (sens antihoraire): 2 cas. De plus, le croisement peut se produire au plus proche ou parfois en contournent
le brin d'extrémités: 2 cas. Potentiellement: 2x2x2x2 = 16 situations à analyser une
par une pour dénombrer les cas possibles ou impossibles. |
|
|
||
|
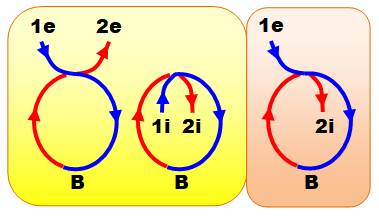
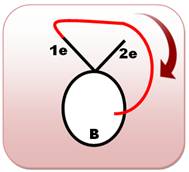
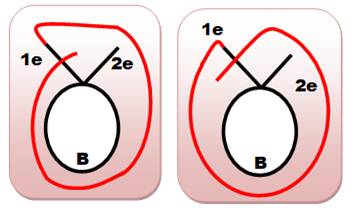
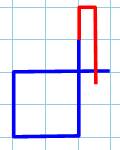
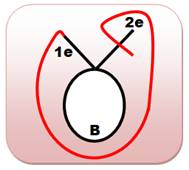
Prolongement dans le sens
antihoraire Il s'agit
d'allonger la courbe pour créer un deuxième croisement. Par exemple (en rouge): un prolongement de 1e et
croisement avec la boucle B. Le
prolongement de 2e et croisement avec B est de même nature. Les deux cas se
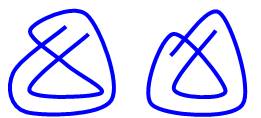
superposent (symétrie). Toutes en bas,
autres représentations courantes de ce genre de graphe. |
|
|
|
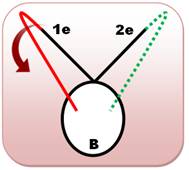
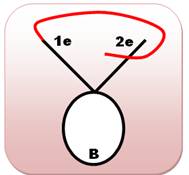
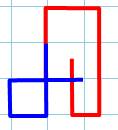
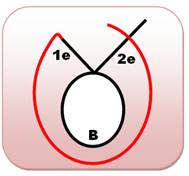
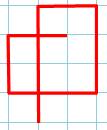
Prolongement dans le sens horaire Il s'agit
d'allonger la courbe dans l'autre sens (sens des aiguilles de la montre) et
former un croisement avec la boucle. Dans ce
cas, il y a formation d'une nouvelle boucle qui encercle 2e. C'est bien un
nouveau cas. Un départ de 2e produirait un cas symétrique. Bilan: deux cas de
croisements avec la boucle et une extrémité externe. |
|
|
|
X2 – Une seule extrémité
externe qui se croise |
|
|
|
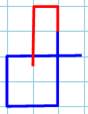
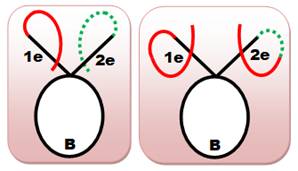
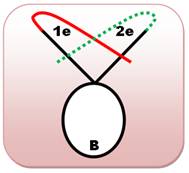
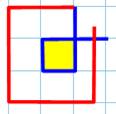
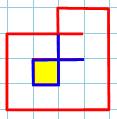
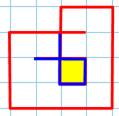
Prolongement au plus près Dans le sens horaire Partant
d'une extrémité, on prolonge la courbe pour croiser la même extrémité (figure de gauche). Les deux cas (rouge et vert) sont identiques par
retournement et superposition. Dans le sens antihoraire Même
principe; un seul cas du fait de la symétrie Comparaison Les deux
cas (horaire et antihoraire) sont différents comme le montre les figures du bas: les extrémités sont du même côté ou
de part et d'autre. |
|
|
|
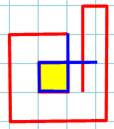
Prolongement par contournement Même principe
que ci-dessus, mais en allant chercher le croisement par contournement. La boucle
initiale est encerclée par une nouvelle boucle. Bilan: quatre cas de
croisements sur une extrémité externe. |
|
|
|
|
||
|
Prolongement dans le sens horaire Partant
d'une extrémité, on prolonge la courbe pour croiser l'autre extrémité au plus
près. Les deux
cas (rouge et vert) sont identiques par retournement et superposition. Idem avec contournement En
croisant le brin 2 par l'autre côté, un nouveau cas est recevable (figures de droite). |
|
|
|
Prolongement dans le sens antihoraire En
partant de 1e et dans le sens
antihoraire, il y a création d'une boucle encerclant la première boucle. Ce cas
est nouveau. Son symétrique partant de 2e
lui est superposable. Idem avec contournement Notez:
impossible de prolonger la courbe pour entourer une nouvelle fois la boucle
car le brin de courbe à atteindre serait enfermé dans la boucle et
inatteignable. Bilan: Soit
quatre cas de croisements entre les deux extrémités externes. |
|
|
|
|
||
|
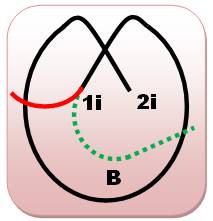
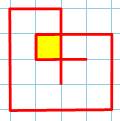
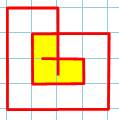
Prolongement pour croiser la boucle Partant de 1i
(extrémité interne), on prolonge pour croiser la courbe. La route peut être
quelconque, sens horaire ou antihoraire; et, comme précédemment, le départ de
2i produit des figures symétriques. Bilan: un seul cas de
croisement avec la boucle et une extrémité interne. Mais, il est identique au premier
cas examiné |
|
|
|
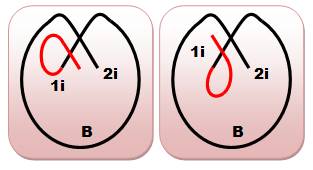
Prolongement pour se croiser
soi-même Partant
de 1i (extrémité interne), on prolonge pour croiser le même brin. Deux
possibilités selon le sens. Les extrémités se retrouvent du même côté ou de
part et d'autre. Toujours
la même remarque pour la symétrie avec un départ en 2i. Bilan: deux cas de
croisements sur une extrémité interne. Mais, ils sont identiques à deux cas
déjà vus. (Voir le tableau de synthèse). |
|
|
|
Prolongement pour croiser l'autre
brin Partant
de 1i, on prolonge pour croiser l'autre brin. Deux possibilités selon que le
brin est croisé directement ou par contournement. Un seul
sens de rotation est possible. Symétrie
en partant de 2i. Bilan: deux cas de
croisements sur les deux extrémités. |
|
|
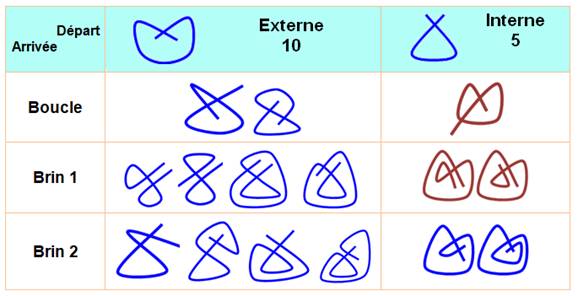
Récapitulatif pour deux croisements
|
Nous avons
dénombré 15 possibilités de double-croissement: 10 à partir des brins
externes et 5 avec les brins internes dont 3 sont communs aux précédents (en marron). Bilan:
12 cas de bi-croisements irréductibles.
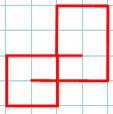
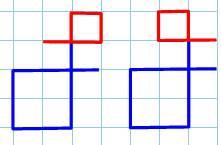
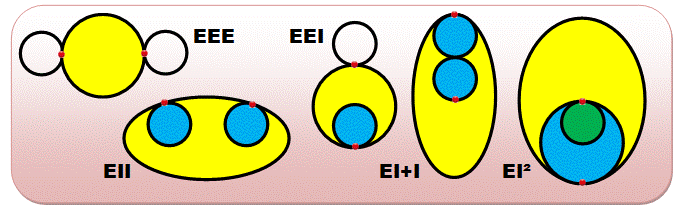
Les cinq
circuits fermés bisécants (représentation stylisée)
Idée de
suite
|
![]()
|
|
|||
|
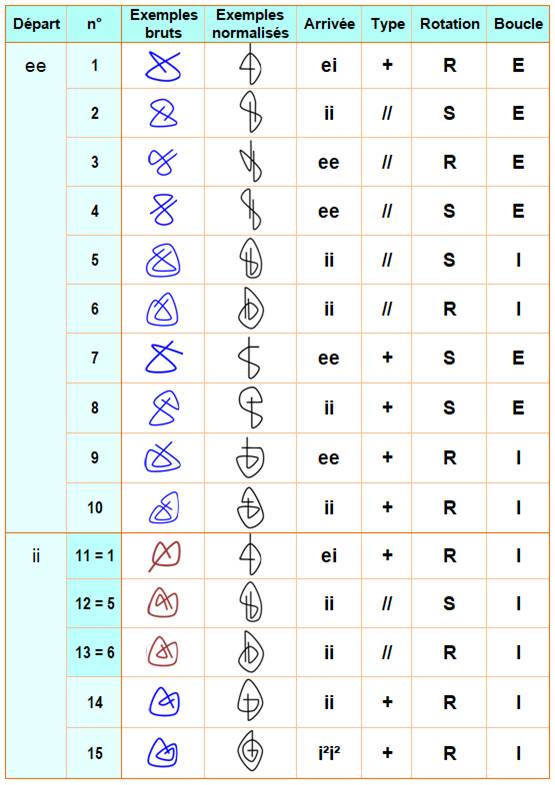
Comment distinguer chacun des cas et s'assurer que
chacun est unique d'un point de vue topologique. Numérotation: de 1 à 15. Motifs: ils sont
rappelés tels que vus ci-dessus et une colonne les reprend en les normalisant
(départ de boucle identique). Départ: ee et ii pour
les deux extrémités externes ou internes à la boucle. Arrivée: même symbole
selon que l'extrémité est externe ou interne. Rotation: un seul sens
de rotation (R), ou deux (S , comme courbe en S). Boucle: les deux
boucles sont externes (E) ou l'une et dans l'autre (I). Type d'extrémités: selon que les
deux extrémités sont "parallèles" ou croisées. Une extrémité dans une double boucle est notée
i². Pour plus de croisements, peut-être faudra-t-il
faire intervenir l'appartenance de l'extrémité à une boucle particulière. |
|
||
|
Bilan |
Parmi les
15 cas recensés, il se trouve que trois d'entre eux sont redondants (ocres). Les douze
cas qui subsistent sont qualifiés de manière unique. |
||
|
Commentaire |
Est-il
possible de simplifier la recherche des invariants à chaque cas ? Il est
clair que la caractérisation présentée ne constitue pas une synthèse
éblouissante. Elle n'est guère propice à une généralisation et encore moins à
une programmation. |
||
Il est étonnant que l’on puisse voir de 20 façons différentes
le paysage sur des chemins qui n’ont qu’un
seul point de rencontre !
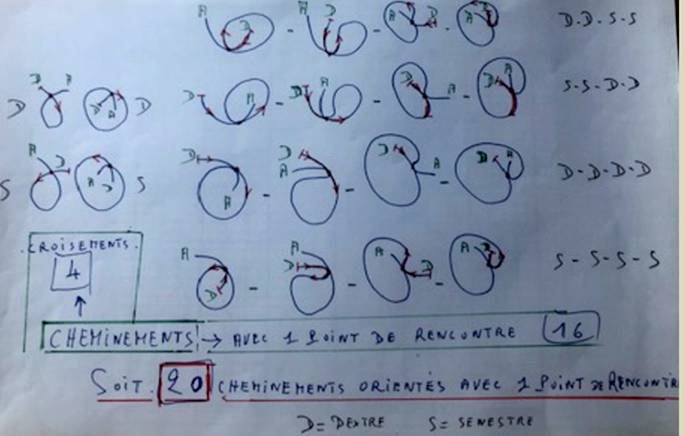
Une remarque proposée
par Gilbert Chovin
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Rien sur
le sujet de cette page, voir néanmoins:
|
|
Cette page |
![]()