|
|||||||||||||||||||||||||||||||||
![]()
|
Puissances de nombres comportant tous
les chiffres Quel est le plus
petit carré qui contient tous les chiffres de 1 à 9 pannumériques)
? Le cube ? La puissance quatrième ? |
|
|
||
|
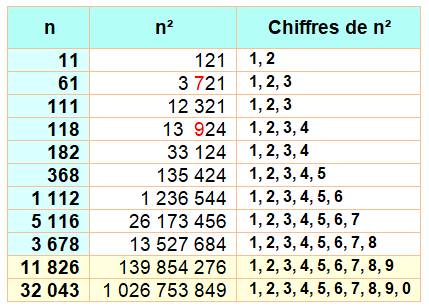
Il faut aller jusqu'au carré de 11 826 pour avoir
un nombre qui contient tous les chiffres de 1 à 9. En prime, ils n'y sont
qu'une seule fois. Il faut le triple (ou presque) pour avoir le 0 en
plus. En rouge: les carrés qui contiennent d'autres
chiffres que ceux spécifiés. 61² est formé avec 1, 2, 3 comme prévu, mais il y a un 7 en plus.
Alors que 111² n'est formé qu'avec 1, 2 et 3. Pourquoi le chiffre 0 in fine ? Tous simplement du fait qu'il est présent dès 10² = 100. |
Chiffres des carrés pour arriver progressivement
à un carré qui contienne tous les chiffres
|
|
Voir Autres
carrés pannumériques
|
|
||
|
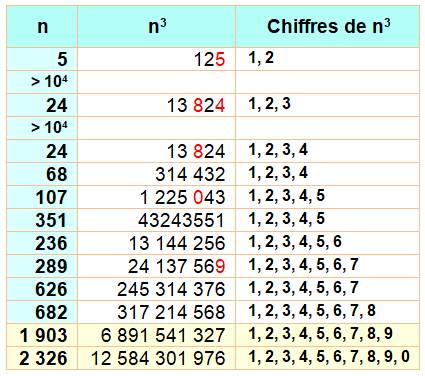
En jaune, les plus petits cubes avec les chiffres
de 1 à 9, puis de 0 à 9. En rouge, les cubes où les chiffres spécifiés
sont bien là, mais avec d'autres chiffres en trop. Pour {1, 2} et {1, 2, 3} pas de solutions avant
le cube de 10 000. |
Chiffres des cubes pour arriver progressivement à
un carré qui contienne tous les chiffres
|
|
![]()
Bilan pour les
puissances de 2 à 12
Lecture: 11 826² est le
plus petit carré avec les chiffres de 1 à 9
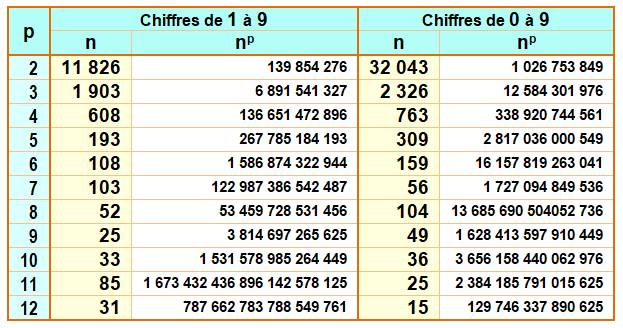
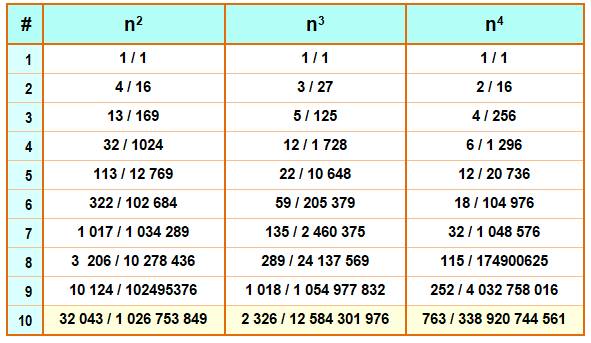
Tableau donnant les
plus petites puissances pour une quantité donnée (#) de chiffres
Lecture: 1 017² = 1 034
289 contient sept chiffres: {0, 1, 2, 3, 4, 8, 9}
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/MOTIF/Pannum/PuisPanu.htm |
![]()