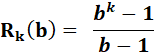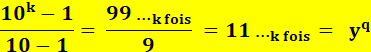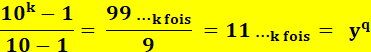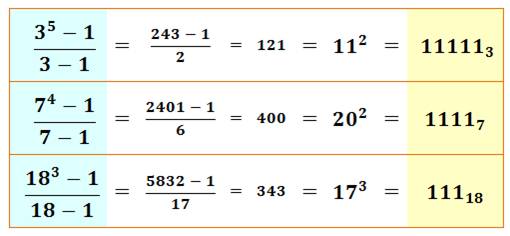NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/09/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	NOMBRES & MOTIFS
Débutants Chiffre	Nombres UNIFORMES				Glossaire Chiffre
INDEX Formes et motifs Nombres en chiffres Chiffres Types de nombres	Repdigits	Repunits		Presque repdigit
	999 …	Division des Repunits		Division de 999 …
	888 …	111 111	Facteurs	Produits
	Nombres Demlo	Nombres dissécables		Suite en 371, 3711 …
	Bi-repdigit	(n.p) min = Repdigit		Nombres trompeurs
		Sommaire de cette page >>> Approche >>> Divertissements >>> Repunit et bases >>> Factorisation >>> Repunits premiers >>> Différence de carrés >>> Repunits en puissance >>> Un tableau amusant ! >>> Somme des repunits

NOMBRES UNIFORMES en 1

ou

REPUNITS ou nombres POLYMONADIQUES

Exemple: 111 = 3 x 37

Les nombres uniformes ou repunits sont composés uniquement du chiffre 1 (concaténation des chiffres 1).

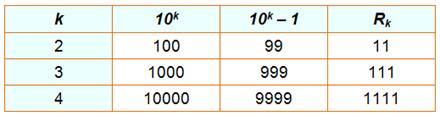
Leurs multiples, formés tous du même chiffre, sont les repdigits.

En base décimale, un repunit vaut: 999… / 9 = (10^k – 1) / (10 – 1)

En base b, un repunit généralisé vaut: (b^k – 1) / (b – 1)

Anglais Rep-unit ou Repunit, nom dû à Beiler en 1966

Prends l'âge que tu avais en 2011, ajoute le nombre formé des deux derniers chiffres de ta date de naissance. Pour tous les individus sur Terre, la somme sera 111.

Exemple: je suis né en 1947 et j'ai 64 ans en 2011: 47 + 64 = 111.

Voir Jeux

Approche

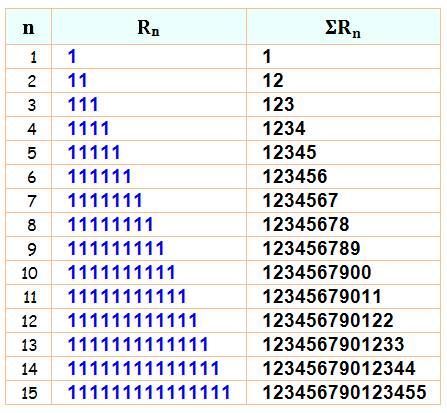
Nombre composé que de 1, comme 111 111 Notation: 113 = 111 Ces sont des palindromes particuliers. On remarque que 111 = 100 + 10 + 1. D'où la forme générique des repunits: 11n = 10^0 + 10^1 + 10^2 + … + 10^n Somme des puissances de 10 En binaire, un repunit est égal à une puissance de 2 moins 1. 1112 = 10002 – 1 Voir Propriété des puissances de 2 En base 9, les repunits sont des nombres triangulaires.

Puissances palindromiques des repunits

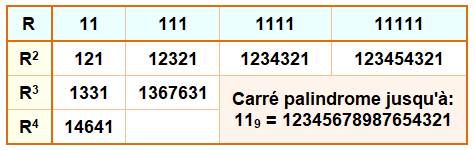
Voir Palindrome / Repunit

Divertissements

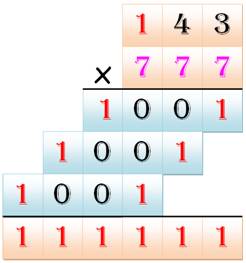
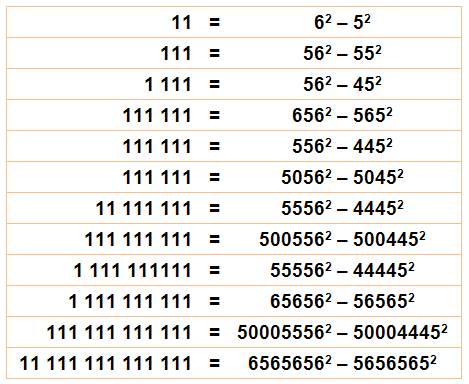
Joli façon de former des repunits Autre présentation Voir Pépites Multiplication produisant un repunit Voir Multiplications en puzzles La racine carrée des pannumériques donne des repunits = 1111111111,11111111010 5555555555555555100541 666666666666254879097 222222221 … Voir Nombres zèbre Fractions en 11 1 / 11 = 0,09 09 … 2 / 11 = 0,18 18 … 3 / 11 = 0,27 27 … 4 / 11 = 0,36 36 … … n / 11 = pour n de 1 à 9 10 / 11 = 0,90 90 … 11 / 11 = 1 12 / 11 = 1,09 09 … Fractions en 111 10 x 1 / 111 = 0,090 090 … 10 x 2 / 111 = 0,180 180 … 10 x 3 / 111 = 0,270 270 … 10 x 4 / 111 = 0,360 360 … … 10 x n / 111 = pour n de 1 à 9 10 x 10 / 111 = 0,900 900 … 10 x 11 / 111 = 0,990 990 … 10 x 12 / 111 = 1,081 081 … Voir Nombres 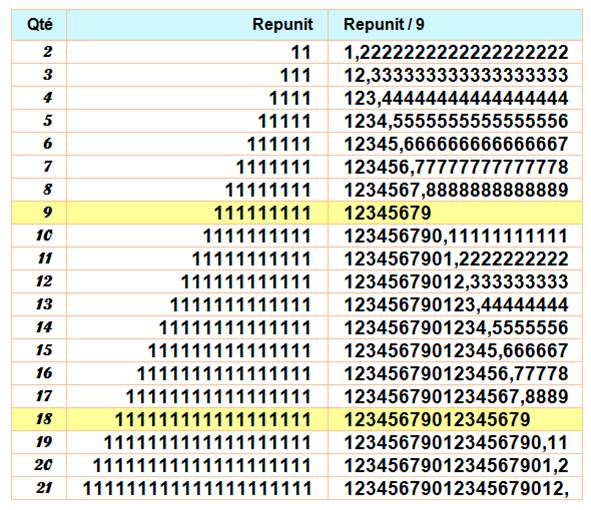périodiques La division par 9 donne la suite des chiffres (en sautant le 8) Voir Nombre de Lewiss Carroll / Repunit et division par 7

REPUNITS en base de numération
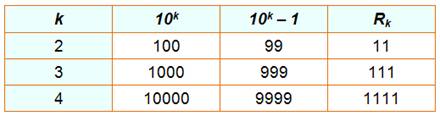
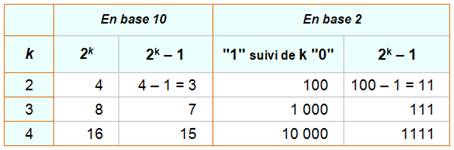
En base 10 Rk = (10^k – 1) / 9 En base 2 Rk = 2^k – 1 Les nombres de Mersenne exprimés en binaire sont des repunits. En base b Un repunit généralisé en base est défini par la relation: Exemple: R2(5) = (5² – 1) / (5 – 1) = 6 ou 1115

FACTORISATION des repunits

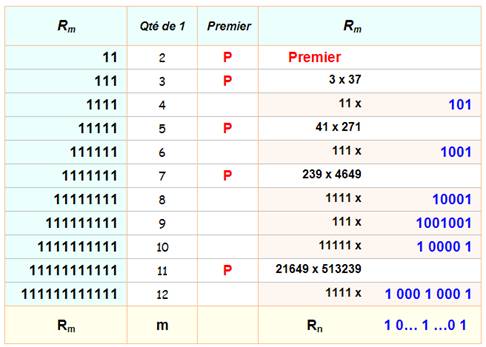
Exemples 111 = 3 x 37 1 111 = 11 x 101 11 111 = 41 x 271 111 111 = 11 x 10101 = 111 x 1001 1 111 111 111 111 111 = 17 x 65 359 477 124 183 Voir Repunit 111 111 / Tables des facteurs des repunits Multiplications magiques Exemple: 37 037 x 3 = 111 111 Le tableau se poursuit avec les repdigits suivants en prenant les multiples des nombres indiqués dans le tableau. Voir Nombres têtus Divisibilité Tout repdigit à nombre pair de chiffres est divisible par 11. Tout repdigit à nombre de chiffres multiple de trois est divisible par 3; divisible par 37; et divisible par 111. Tout repdigit à nombre de chiffres multiple de six est divisible par 3, 7, 11, 13, 37 et tous leurs produits. Voir Table des facteurs des repunits Voir Division des repunits par les repunits

REPUNITS PREMIERS

Les cinq seuls repunits premiers connus, et cela pour Rn avec n jusqu'à au moins n = 30 000: Certains auteurs ne donnent le nom de repunit qu’à ces nombres premiers. Le dernier a été découvert en 1986 par Williams et Dubner. Un repunit ne peut être premier que si son nombre de chiffres est premier. On conjecture que les repunits (premiers) sont en nombre infini. R49 081 = (10^49 081 – 1) / 9 = 11 …11 (48081 fois le 1) est pseudo-premier; il est probablement premier. Harvey Dubner - 1999 On pense que les trois suivants sont premiers: R86 453 (Baxter – 2000), R109 297 (Dubner – 2007) et R270 343 (Vozny et Budnyy – 2007). Pour être premier, un repunit doit nécessairement comporter un nombre premier de 1. Les nombres 2, 19, 23, 317 & 1 031 sont effectivement premiers. La réciproque n'est pas vraie! La démonstration est basée sur une généralisation du motif: Rm = R n x 10…1…01 (en bleu dans le tableau). En base 2, un repunit s’exprime par: Rp = 2^p – 1. Or : 2^p – 1 est premier si et seulement si 2^p – 1 divise S(p-1) avec S(1) = 4 et S(n+1) = S(n)² – 2. Voir Primalité des nombres de Mersenne / Premiers à éros / Presque repdigits premiers

Différence de Carrés
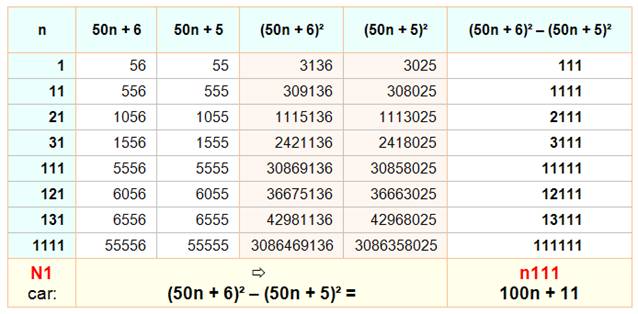
Approche Utilisation de la différence de carrés de nombres proches dont la différence donne toujours un nombre terminé par 11. Application aux repunits Voir Différence de carrés

REPUNITS EN PUISSANCE

Un repunit n’est ni carré, ni cube, ni puissance 5^e. S'il existe des repunits en puissances pures, ils sont plus rares que les repunits premiers. Seuls x / log(x) entiers compris entre 0 et x sont des nombres premiers; et Seuls x entiers compris entre 0 et x sont des puissances pures. En réalité en 2009, on a démontré que Aucun repunit n'est jamais une puissance parfaite. De même: Aucun nombre en 1 0k 1 0k 1 n'est une puissance parfaite. L'indice k indiquant une séquence de k fois le chiffre "0". Formalisation Le théorème de Bugeaud-Mignotte (2009) affirme qu'un repunit (sauf 1) n'est jamais une puissance parfaite n'a aucune solution pour n, y, q > 1 Démonstration On peut écrire un repunit sous la forme du repdigit en 9, divisé par 9: Rk = (10^k – 1) / 9 Trouver des repunits en puissance pure revient à résoudre l'équation (10^k – 1) / 9 = x^q ou 10^k = 9 x^q + 1 avec x, k et q entiers Étape 1 (principe) On démontre que q doit être inférieur à N. Pour ce, on décompose 9 x^q + 1en facteurs premiers comprenant 2 et 5 (les facteurs premiers de 10). On estime un majorant pour l'exposant de 5 et on démontre que q doit être inférieur à 2063. Étape 2 (principe) On vérifie que, pour toutes les valeurs de q < N, il n'y a pas de solution. Il n'y a que 311 nombres premiers entre 0 et 2063. Soit 311 équations à 2 inconnues à résoudre. On cherche les incompatibilités. Un ordinateur est néanmoins nécessaire Bel exemple de démonstration moderne. Astuces théoriques pour réduire le problème. Et, utilisation de l'ordinateur pour résoudre les cas identifiés restants.

Et dans une autre base?

On conjecture qu'en base b, il n'y a que trois solutions:

Source: Yann Bugeaud - Université de Strasbourg - Pour la Science - mai 1999

Démonstration en An Analytic Proof of Bugeaud-Mignotte Theorem - Jamel Ghanouchi

Voir Nombres brésiliens

Un tableau amusant !

On forme les nombres ondulants palindromes avec les chiffres successifs. On les multiplie par la somme de leurs chiffres. Le résultat est le carré du repdigit formé avec le chiffre central du nombre palindrome.

Tableau impressionnant

Palindromes		Somme des chiffres		Produit		Carrés
11	×	(11)	=	121	=	11²
121	×	(1+2+1)	=	484	=	22²
12321	×	(1+2+3+2+1)	=	110 889	=	333²
1234321	×	(1+2+3+4+3+2+1)	=	19 749 136	=	4444²
123454321	×	(1+2+3+4+5+4+3+2+1)	=	3 086 358 025	=	55555²
12345654321	×	(1+2+3+4+5+6+5+4+3+2+1)	=	444 443 555 556	=	666666²
1234567654321	×	(1+2+…+6+7+6+…+2+1)	=	60 493 815 061 729	=	7777777²
123456787654321	×	(1+2+…+7+8+7+…+2+1)	=	7 901 234 409 876 544	=	88888888²
12345678987654321	×	(1+2+…+8+9+8+…+2+1)	=	999 999 998 000 000 001	=	999999999²

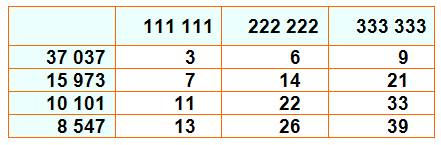
La magie est expliquée avec ce nouveau tableau.

Chaque nombre ondulant est en fait le carré d'un repunit.

Il est multiplié par le carré de la quantité de chiffres. Le produit est le carré du repdigit du même ordre:
111² x 3² = (111 x 3)² = 333².

Et, voilà!

Voir Explication de 1+2+3+4+3+2+1 = 4²

Voir DicoNombre 11, 121, 484, 12 321, 110 889

Tableau réduit et explicatif

Repunit²		Nb		Produit
11²	×	2²	=	22²
111²	×	3²	=	333²
1111²	×	4²	=	4444²
11111²	×	5²	=	55555²
111111²	×	6²	=	666666²
1111111²	×	7²	=	7777777²
11111111²	×	8²	=	88888888²
111111111²	×	9²	=	999999999²

Curiosités avec les cubes

11³ = 1331 & Somme des chiffres = 8 = 2³

111³ = 1 367 631 & Somme des chiffres = 27 = 3³

1111111³ = 137…631 & Somme des chiffres = 64 = 4³

11…11_{9 fois} ³ => Somme des chiffres = 99

11…11_{10 fois} ³ => Somme des chiffres = 100

Voir Nombre doublement cubes / Table des repunits à une puissance

Somme des repunits
La somme des repunits donne les chiffres successifs. Formulation (10^n+1 – 10 – 9 n) / 81 = 1 + 11 + 111 + … + 11…1nfois 2 x (10^n+1 – 10 – 9 n) / 81 = 2 + 22 + 222 + … + 22…2nfois 3 x (10^n+1 – 10 – 9 n) / 81 = 3 + 33 + 333 + … + 33…3nfois 4 x (10^n+1 – 10 – 9 n) / 81 = 4 + 44 + 444 + … + 44…4nfois Etc.

Repunit et information

Voir Automobile

Suite	Autres pages Carrés des repunits Divisibilité par un repunit Kaprekar et repunit Nombres à chiffres répétés Nombres avec des uns (partition) Nombres brésiliens Nombres en 10101 Ondulants Opérations palindromes et repunits Persistance multiplicative du repunit Presque repdigit Puissances de 11 et triangle Pascal Puissances et palindromes en 11, 101, 111 … Repdigit et différence de carrés Suite en 371, 3711 …
Voir	Année 2011 Fermat Multiplication Nombres à motifs Nombres magiques Nombres répétés Nombres zèbre Puissance 11 Somme de puissances successives Suite alternée
DicoNombre	Nombre 11 Nombre 111 Nombre 111 111
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Formes/RepUnit.htm

 Renvoi de liens

Presque repunits premiers