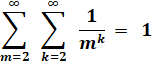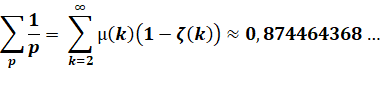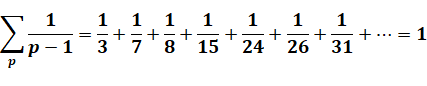|
Édition du: 01/09/2022 |
|
INDEX |
PUISSANCES |
||
|
Nombre
ABA (ABA) |
|||
|
Nombres puissants
(2-P, 3-P) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES PUISSANTS Liste et programme Suite des
nombres représentant une puissance pure et programmes de production de cette
liste. |
||
|
|
Sommaire de cette page >>> Nombres puissants |
Débutants Glossaire |
|
Définition Les nombres puissants sont des nombres dont la
décomposition en facteurs premiers est composées de facteurs tous portés à la
même puissance supérieure à 1. Note: ce sont toutes
les puissances parfaites sans
doublon et incluant le 1. |
Exemples 27 = 33 OUI 100 = 10² = 22 × 52 OUI 500 =
22 × 53 NON |
||
|
Liste jusqu'à 50 000 sans doublons comme 3 |
1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225,
243, 256, 289, 324, 343, 361, 400, 441,
484, 512, 529, 576, 625, 676, 729, 784, 841, 900,
961, 1000, 1024, 1089, 1156, 1225, 1296,
1331, 1369, 1444, 1521, 1600, 1681, 1728, 1764, 1849, 1936, 2025, 2048, 2116,
2187, 2197, 2209, 2304, 2401, 2500, 2601,
2704, 2744, 2809, 2916, 3025, 3125, 3136, 3249, 3364, 3375, 3481, 3600, 3721,
3844, 3969, 4096, 4225, 4356, 4489, 4624, 4761, 4900, 4913, 5041, 5184, 5329,
5476, 5625, 5776, 5832, 5929, 6084, 6241, 6400, 6561, 6724, 6859, 6889, 7056,
7225, 7396, 7569, 7744, 7776, 7921, 8000,
8100, 8192, 8281, 8464, 8649, 8836, 9025, 9216, 9261, 9409, 9604, 9801, 10000, 10201, 10404, 10609, 10648, 10816, 11025,
11236, 11449, 11664, 11881, 12100, 12167, 12321, 12544, 12769, 12996, 13225,
13456, 13689, 13824, 13924, 14161, 14400, 14641, 14884, 15129, 15376, 15625,
15876, 16129, 16384, 16641, 16807, 16900, 17161, 17424, 17576, 17689, 17956,
18225, 18496, 18769, 19044, 19321, 19600, 19683, 19881, 20164, 20449, 20736,
21025, 21316, 21609, 21904, 21952, 22201, 22500, 22801, 23104, 23409, 23716,
24025, 24336, 24389, 24649, 24964, 25281, 25600, 25921, 26244, 26569, 26896, 27000, 27225, 27556, 27889, 28224, 28561, 28900,
29241, 29584, 29791, 29929, 30276, 30625, 30976, 31329, 31684, 32041, 32400,
32761, 32768, 33124, 33489, 33856, 34225, 34596, 34969, 35344, 35721, 35937,
36100, 36481, 36864, 37249, 37636, 38025, 38416, 38809, 39204, 39304, 39601, 40000, 40401, 40804, 41209, 41616, 42025, 42436,
42849, 42875, 43264, 43681, 44100, 44521, 44944, 45369, 45796, 46225, 46656,
47089, 47524, 47961, 48400, 48841, 49284, 49729, 50176, 50625, 50653, … |
||
|
Petits écarts entre deux puissances
successives Seules valeurs pour 1, 2 et 3 et seules valeurs
pour 4 |
1 |
2 |
3 |
4 |
|
|
125, 128 |
4, 8 32, 36 121, 125 125, 128 |
||||
|
Théorie |
En 2002, Preda Mihăilescu, mathématicien
roumain, prouva la conjecture
de Catalan: 8 et 9 sont les seules puissances consécutives. La conjecture de Pillai, non résolue, énonce que:
pour tout entier k, il y a seulement une quantité finie de paires de
puissances dont la différence est k. |
||||
Voir Conjecture
de Pillai – Wikipédia

|
Somme des inverses des nombres
puissants Avec doublons comme 34 = 92
= 81. |
|
|
|
Somme des inverses des nombres
puissants SANS doublons. µ (k) : fonction de
Moebius
|
|
|
|
Théorème de Goldbach-Euler Toutes les puissances parfaites sans le 1 et sans
les doublons. |
|
|
Voir Nombre
0,8744…
|
Programme
|
But Établir la liste des nombres puissants. Commentaires Initialisation. Procédure indiquant si un nombre n est puissant
ou non Pour cela, la liste des exposants (exp) est établie
(seq) et si le PGCD de tous les facteurs est commun et
plus grand que 1, Alors le nombre est puissant. Le programme principal examine les nombres de 1 à
100 (exemple). Si le nombre est puisant, il est placé dans la liste. |
|
|
Programme avancé
|
Commentaires En juin 2011, R. J. Mathar publie ce programme
dans OEIS A001597 – Perfect power. La procédure est la même, c'est du classique. Le programme principal est récursif et emploie les instructions remember qui évite de recommencer les calculs
déjà effectués). Et, l'instruction procname
qui rappelle la procédure sans la nommer. |
|
Voir Programmation – Index
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/PUISSANC/PuisList.htm
|