NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 06/07/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	NOMBRES
Débutants Nombres et Puissances de 10	PUISSANCES				Glossaire Puissances
INDEX Puissance Décomposition	Calculs pratiques		Multi-puissances	Exposants	Consécutives
	Nombres puissants (2-P, 3-P)			Liste des puissants
		Sommaire de cette page >>> Types de nombres "puissants" >>> Cas des nombres de 1 à 100 >>> Listes >>> Quantités >>> Nombres puissants qui différent de 2 >>> Nombres puissants en n² – 1 >>> Nombres en n² + 2

NOMBRES PUISSANTS

Powerful numbers

Nombres qui comportent certaines puissances dans les exposants de leur factorisation.

Voir Nombres puissants, plénipotents … comme introduction à cette page.

Types de nombres "puissants"
Explications Un nombre composé est le produit unique de facteurs. Chacun des facteurs est utilisé une seule fois ou plusieurs fois: S'ils ne sont jamais utilisés deux fois, le nombre est dit sans carré. Avec un facteur au carré, ou plus, c'est un nombre avec carré. Avec tous ses facteurs au carré, ou plus, c'est un nombre puissant. Il est 2-puissant s'il existe un exposant au moins égal à 2; Il est 3-puissant s'il existe un exposant au moins égal à 3; Il est k-puissant s'il existe un exposant au moins égal à k;	Illustration Définition Un nombre est k-puissant si, étant divisible par p, il l'est aussi par p^k. k est l'exposant le plus petit supérieur à 1. Ainsi 200 est 2-puissant. Et, 100 est un carré; il est aussi 2-puissant.

Cas des nombres de 1 à 100
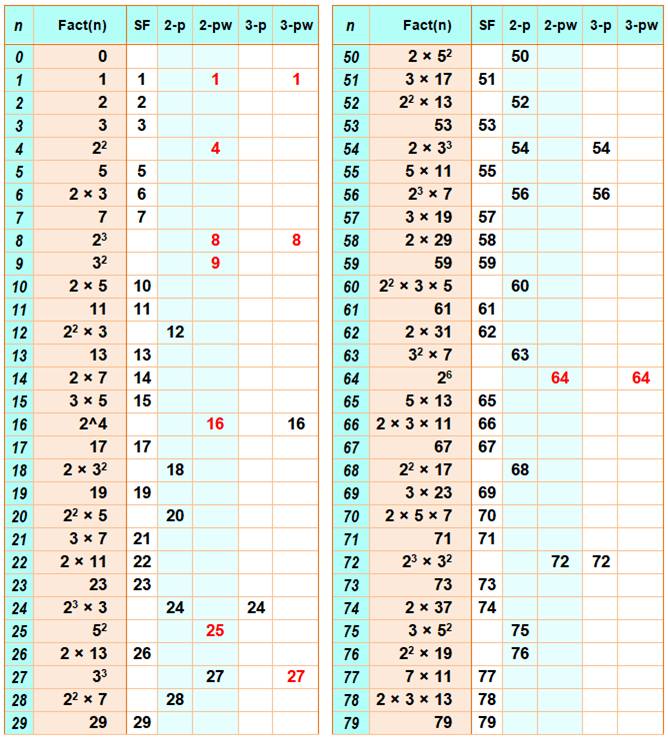
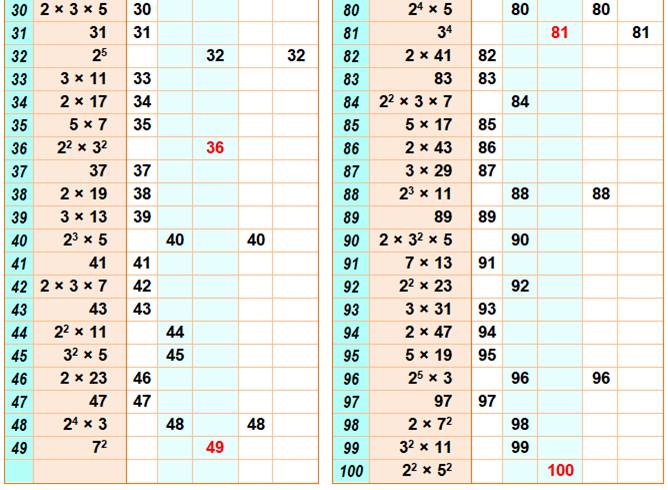
Légende N de 1 à 100 Avec leurs facteurs En rouge les puissances pures	SF = sans carré 2-pw = 2-puissant; autres 2-p avec un carré; 3-pw = 3-puissant; autres 3-p avec un cube;

Listes
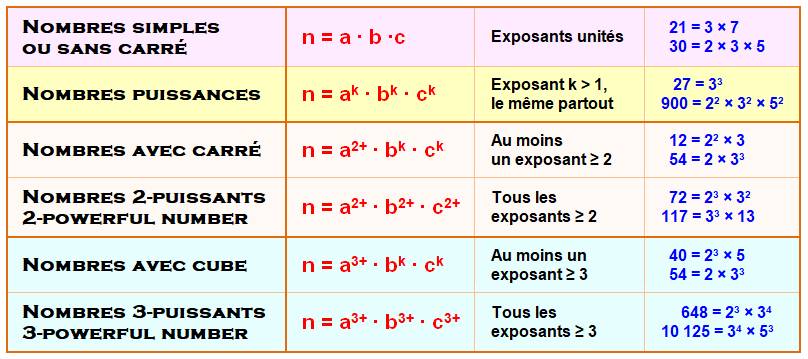
Nombres simples ou sans carré	1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 33, 34, 35, 37, 38, 39, 41, 42, 43, 46, 47, 51, 53, 55, 57, 58, 59, 61, 62, 65, 66, 67, 69, 70, 71, 73, 74, 77, 78, 79, 82, 83, 85, 86, 87, 89, 91, 93, 94, 95, 97, 101, … >>>
Nombres puissances	1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225, 243, 256, 289, 324, 343, 361, 400, 441, 484, 512, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1000, … >>>
Nombres puissants	1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 72, 81, 100, 108, 121, 125, 128, 144, 169, 196, 200, 216, 225, 243, 256, 288, 289, 324, 343, 361, 392, 400, 432, 441, 484, 500, 512, 529, 576, 625, 648, 675, 676, 729, 784, 800, 841, 864, 900, 961, 968, 972, 1000, 1024, 1089, 1125, 1152, 1156, 1225, 1296, 1323, 1331, 1352, 1369, 1372, 1444, 1521, 1568, 1600, 1681, 1728, 1764, 1800, 1849, 1936, 1944, 2000, 2025, 2048, 2116, 2187, 2197, 2209, 2304, 2312, 2401, 2500, …
Nombres puissants mais non-puissances	72, 108, 200, 288, 392, 432, 500, 648, 675, 800, 864, 968, 972, … Ex: 72 = 2^3 × 3^2 / 108 = 2^2 × 3^3
Nombres avec carré et non 2-puissant	12, 18, 20, 24, 28, 40, 44, 45, 48, 50, 52, 54, 56, 60, 63, 68, 75, 76, 80, 84, 88, 90, 92, 96, 98, 99, 104, 112, 116, 117, 120, 124, 126, 132, 135, 136, 140, 147, 148, 150
Nombres puissants ou Nombres 2-puissants 2-powerful number	1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 72, 81, 100, 108, 121, 125, 128, 144, 169, 196, 200, 216, 225, 243, 256, 288, 289, 324, 343, 361, 392, 400, 432, 441, 484, 500, …
Nombres avec cube et non 3-puissant	24, 40, 48, 54, 56, 72, 80, 88, 96, 104, 108, 112, 120, 135, 136, 144, 152, 160, 162, 168, 176, 184, 189, 192, 200, 208, 224, 232, 240, 248, 250, 264, 270, 272, 280, 288, 296, 297, 304, …
Nombres 3-puissants 3-powerful number	1, 8, 16, 27, 32, 64, 81, 125, 128, 216, 243, 256, 343, 432, 512, 625, 648, 729, 864, 1000, 1024, 1296, 1331, 1728, 1944, 2000, …

Quantités de nombres k-puissant par plage en 10^k

Plage	2-p	3-p	4-p	5-p
10	49	216	625	2 048
100	3 136	52 488	583 443	5 038 848
1 000	253 472	25 153 757
10 000	23 002 083	16 720 797 973

Exemple: 216 est le dixième nombre 3-puissant

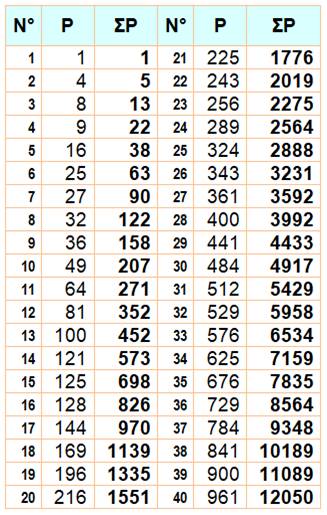
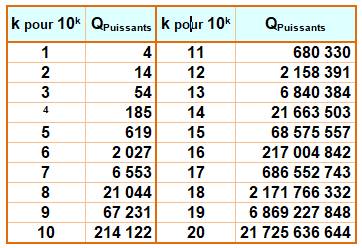
Somme cumulative des nombres puissances	Quantité de nombres puissants par plages en puissances de 10
	Exemple de lecture k = 2 => il y a 14 nombres puissants jusqu'à 10² = 100: il sont 54 jusqu'à 1000.

Voir Somme des puissances

Nombres puissants qui différent de k
Il existe une infinité de couples de nombres puissants consécutifs. Les couples qui différent de deux unités sont rares. Il n'existe pas trois nombres puissants consécutifs – Conjecture d'Erdös	Nombres puissants ave écart de 1 jusqu'à 100 000 8 / 9, 288 / 289, 675 / 675, 9 800 / 9 801, 12 167 / 12 168 Nombres puissants ave écart de 2 25, 70 225, 130 576 327, 189 750 625, 512 706 121 225, 13 837 575 261 123, 99612 037 019 889, … Nombres puissants ave écart de 3 1, 125, 1 369 (seuls jusqu'à 10 millions).

Voir OEIS A076445 – The smaller of a pair of powerful numbers that differ by 2.

Nombres puissants en n² – 1
Liste des nombres puissants en n² – 1 .	3 17 26 99 485 577 1 351 3 363 19 601 24 335 70 226 114 243 470 449 665 857 930 249	9 289 676 9 801 235 225 332 929 1 825 201 11 309 769 384 199 201 592 192 225 4 931 691 076 13 051 463 049 221 322 261 601 443 365 544 449 865 363 202 001	2^3 2^5 • 3^2 3^3 • 5^2 2^3 • 5^2 • 7^2 2^3 • 3^5 • 11^2 2^7 • 3^2• 17^2 2^4 • 3^3 • 5^2 • 13^2 2^3 • 29^2 • 41^2 2^5 • 3^4 • 5^2 • 7^2 • 11^2 2^5 • 3^2 • 13^2 • 23^3 3^5 • 5^2 • 17^2 • 53^2 2^^3 • 13^4 • 239^2 2^5 • 3^5 • 5^2 • 11^2 • 97^2 2^9 • 3^2 • 17^2 • 577^2 2^4 • 5^3 • 11^2 • 31^2 • 61^2

Nombres puissants en n² + 2
Liste des nombres puissants en n² + 2 Ils sont en quantité infinie (F. Luca).	5 265 13 775 716 035 9 980 583 37 220 045	27 70 227 1897 50 627 512 706 121 227 99 612 037 019 891 1 385 331 749 802 027	3^3 3^5 • 17^2 3^3 • 11^2 • 241^2 3^3 • 41^2 • 3361^2 11^3 • 273 569^2 3^7 • 17^2 • 46 817^2

Voir OEIS A175180 – Numbers n such that n^2 + 2 is powerful

Suite	Nombres puissants jumeaux (question au Bac) Nombres sans et avec facteurs carrés Nombres puissants ou plénipotents Nombres puissants au bac Exposants à étages Nombres idéonaux Nombres multi-puissants Puissances et chiffres permutés Puissances et racines Puissances – Table de valeurs
Voir	Puissance – Index Puissances de 2 Puissances de 2 à 5
Site	OEIS A001694 - Powerful numbers, definition: if a prime p divides n then p^2 must also divide n (also called squareful, square full, square-full or 2-powerful numbers). Powerful Numbers – Wolram MathWorld
Cette page	http://villemin.gerard.free.fr/aNombre/PUISSANC/Powerful.htm