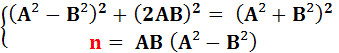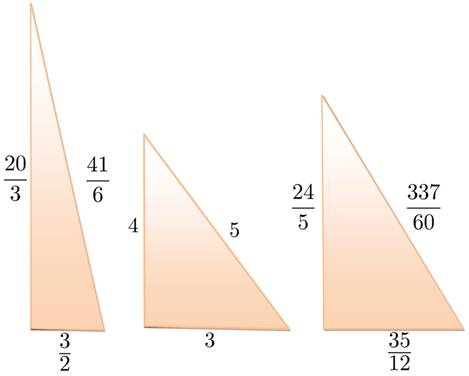
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/10/2011 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Type de nombres
Débutants Nombres	Nombres congruents				Glossaire Nombres
INDEX Nombres	Présentation	Valeurs	Propriétés	Historique
			Formule
		Sommaire de cette page >>> Nombres 5, 6 et 7 >>> Valeur des côtés du triangle rectangle >>> Liste pour n < 500 >>> Nombres congruents "entiers" >>> Nombres 53, 101, 157

NOMBRES CONGRUENTS

Valeurs

Un nombre congruent est une aire en nombre entier d'un triangle rectangle dont les côtés ont des mesures rationnelles. Plusieurs catégories:

Type "général": tous sans distinction;

Type "entier": tels que les mesures des côtes sont des nombres entiers

Type "primitif": en éliminant tous ceux qui sont multiples d'un autre

NOMBRES 5, 6 et 7 – Les trois plus petits
5 6 7

Voir Triangle 345

Valeur des côtés du triangle rectangle
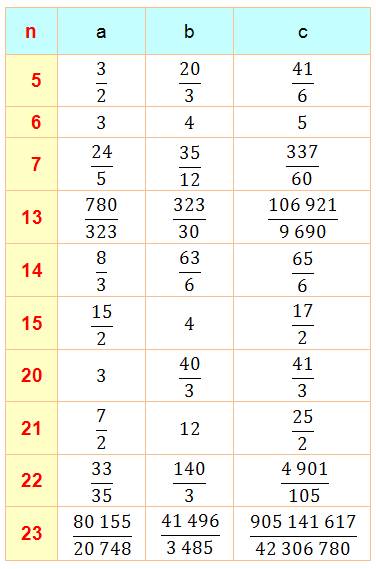
Autres valeurs 34; 17/6, 24, 165/6 41; 123/20, 40/3, 881/60 65; 65/6, 12, 97/6 210; 21, 20, 29

Voir Historique pour ces nombres / Autres valeurs

Tous les nombres congruents <500
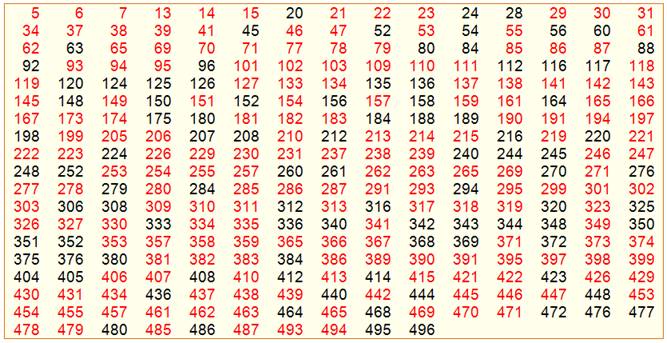
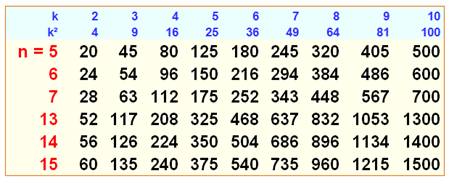
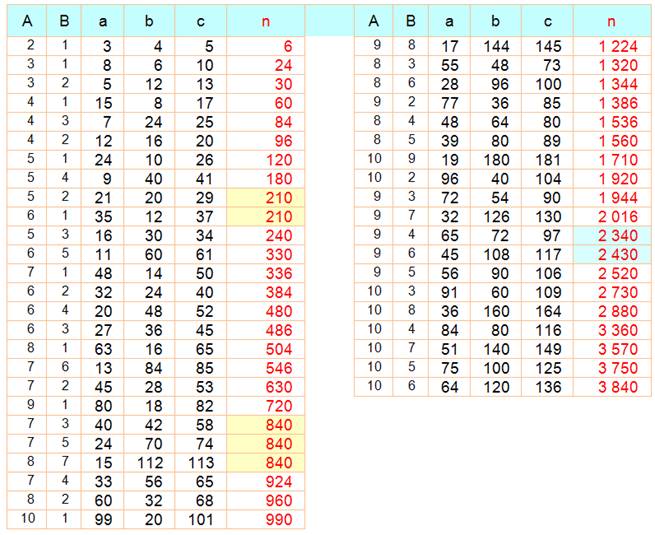
En rouge les nombres congruents primitifs; les autres sont des multiples au carré des primitifs. Retrouvez toutes ces valeurs dans le DicoNombre Nombres primitifs en rouge et leurs multiples en k² (de 5 à 15)

Liste de nombres congruents "entiers"

Ne serait-ce que par les exemples, nous avons qu'il suffit de donner les deux côtes à angle droit (X et Y) pour déterminer l'hypoténuse et l'aire du triangle rectangle. Conséquence, deux nombres suffisent pour créer un nombre congruent. Ils obéissent à la relation suivante: Liste des nombres congruents "entiers" avec nombres entiers pour les côtés du triangle rectangle; et pour A et B jusqu'à 10. En jaune, les nombres congruents engendrés de plus d'une façon. Attention, c'est loin d'être la liste de tous les nombres congruents. Eh, oui, le nombre 5 par exemple, n'est pas apparu. En effet, le nombre congruent 5 nécessite des nombres fractionnaires comme mesures des côtés. et des nombre irrationnels pour A et B. Par un calcul à l'envers, on trouve que les valeurs de A et B seraient: et Même de petites valeurs entières de nombres congruents peuvent attendre longtemps avant d'apparaître dans cette table. Exemples classiques avec les nombre 53, 101 ou encore 157.

Voir Autres formules

Nombre 53
A = 18 73 180 325 B = 11 58 313 156 qui produisent le nombre congruent: 53 x 2² x 3² x 5² x 7² x 11² x 13² x 17² x 29² x 41² x 18 353² x 26 737² c'est-à-dire, le nombre congruent primitif 53, en retirant les carrés.

Voir Nombre 53

Nombre 101

Plus petite solution trouvée pour 101 par Bastien en 1914: On vérifie que A² + B² = C² et que AB/2 = 101. Avant simplification, les fractions se présentent comme suit: A = 711024064578955010000 / 118171431852779451900; B = 3967272806033495003922 / 118171431852779451900; C = (2 x 2015242462949760001961) / 118171431852779451900; Wolfram donne la définition suivante: un nombre a est congruent obéit aux relation suivantes: De sorte que pour 101, ces paramètres sont (solution minimale): x = y = z = t =

Voir Nombre 101

Nombre 157
Trouvé par Zagier, avec les côtés du triangle rectangle qui valent:

Voir Nombre 157

Suite	Nombres congruents – Propriétés
Voir	Addition - Glossaire Briques de Pythagore Congruence, modulo Pythagore – Biographie Triangle de Pythagore Triangle rectangle
Diconombre	Nombre 5 Nombre 6 Nombre 7
Cette page	http://villemin.gerard.free.fr/aNombre/TYPADD/CongVal.htm