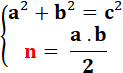|
||||||||||||||||||||||||||||||||||||||||
![]()
|
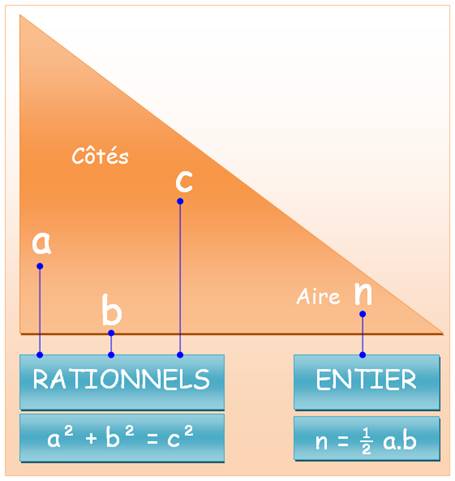
NOMBRES CONGRUENTS Nombres entiers mesurant l'aire de triangles rectangles
dont les côtés ont des mesures entières ou rationnelles.
Oui! Un petit air de famille avec
les triplets de
Pythagore … |
|
La terminologie
n'est pas très appropriée. Elle remonte à Fibonacci
qui parlait de congruence au sens latin de congruere: concorder, aller ensemble. >>> |
|
|
|
|
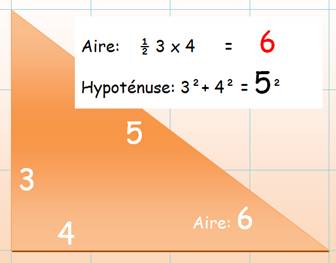
Deux triangles en
exemple
Le nombre 6 issu de telles propriétés est dit nombre congruent.
Voir Triangle isiaque
|
|
Voir Liste
|
|
|
|
Définition classique
Si a, b et c sont les mesures des côtés du
triangle rectangle, avec c pour l'hypoténuse, alors un nombre
congruent n est tel que le système suivant:
a des solutions avec n entier et a, b et
c des rationnels. Définition
équivalente
Les trois carrés forment une progression
arithmétique, comme par exemple
u² + n – v² – n = v² – w² u²
+ w² = 2 v² Ce qui veut dire qua la recherche des nombres
congruents consiste aussi à trouver les sommes de deux carrés qui égalent le double d'un carré. Suite >>> Autres définitions
|
|
Voir Propriétés des
nombres congruents
Les premiers nombres congruents
|
5, 6, 7, 13, 14, 15, 20, 21, 22, 23,
24, 28, 29, 30, 31, 34, 37, 38, 39, 41, 45, 46, 47, 52, 53, 54, 55, 56, 60,
61, 62, 63, 65, 69, 70, 71, 77, 78, 79, 80, 84, 85, 86, 87, 88, 92, 93, 94, 95,
96, 101, 102, 103, 109, 110, 111, 112, 116, 117, 118, 119, 120, 124, 125,
126, … |
|
|
|
|
Un nombre congruent sans facteur
carré est dit primitif. Il est d'usage
de ne considérer comme nombres congruents que
ceux sans facteur carré.
|
|
Voir Liste
|
Il y a environ 1000 ans, le mathématicien persan Al
Karaji a cherché pour la première fois combien de nombres congruents
pouvaient existerer. Il a fallu encore plusieurs millénaires pour que les
cent premiers nombres congruents soient découverts. En 2009, toutefois, les superordinateurs avaient
découvert les 3 148 379 694 premiers nombres congrus. Certains de ces nombres
sont si énormes que si leurs chiffres étaient écrits sous forme décimale, ils
s’allongeraient jusqu’à la Lune. |
|
|
||
|
The
question of determining whether a given rational number is a congruent number
is called the congruent number problem. An
integer n is a congruent number if there exists a right triangle with rational
sides so that the area of the triangle is n. One of
the oldest unsolved problems in mathematics is to determine the congruent numbers. In number
theory, one often comes across problems
which arise naturally and are easy to pose,
but whose solutions require very sophisticated methods. What is known as
"The congruent number problem" is one such. Its statement is very simple and the problem dates back to Antiquity, but it was only
recently that a breakthrough was made,
thanks to current developments in the arithmetic of elliptic curves. |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
![]()