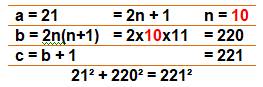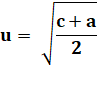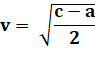|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
TRIPLETS de PYTHAGORE Génération Il existe diverses
formules pour trouver un triplet de Pythagore. Mais, la formule la plus
générale est celle-ci: (u² – v²,
2uv, u² + v²) La solution générale en nombres entiers de l'équation a² + b² = c² avec a>0, b>0 et c>0 a et b étant étrangers (premiers entre eux)est a = u² – v², b = 2uv, c = u² + v²u, v sont des entiers positifs étrangers de parité opposée.Cette solution engendre tous les triplets primitifs
Note: si vous pensez que la formule
n'atteint pas le triplet (9² + 12² = 15²), c'est que le triplet n'est pas
primitif; simplifié par 3, son associé primitif est le fameux: 3² + 4² = 5². |
Preuve – Vérification

|
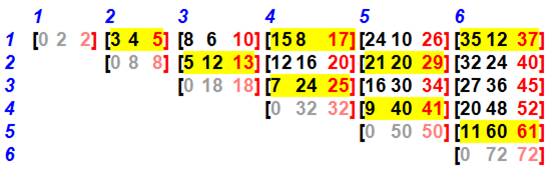
Observations Ces triplets comme 5² + 12² = 13² sont
particuliers en ce qu'ils comprennent deux nombres consécutifs. Voir le tableau Formule Pour tout n, les trois nombres suivants forment
un triplet de Pythagore.
Trouver b et c pour a = 21
Ou plus
directement : b = 1/2 (a² – 1 ) |
Triplets jumeaux (Twin
triples)
|
||
|
Justification |
|
||
|
Notez a² = c² –
b² |
b + c = 2n² + 2n + 2n² + 2n + 1 = 4n² + 4n
+ 1 = (2n + 1)² = a² Autrement-dit: dans le tableau, on lit directement: 12 + 13 = 25, 24 +
25 = 49 … Aussi: Tous les nombres impairs au carré sont différence de deux
carrés successifs: Ex: 11² = 61² – 60² = 61 + 60 = 121 |
||
Voir Triplets
jumeaux
|
|
|||
|
Méthode
NB: tout nombre impair est générateur d'un
triplet. |
n 1/2 (n² –
1) 1/2 (n² +
1)
|
=
5 =
1/2 (25 – 1) = 12 =
1/2 (25 + 1) = 13 |
|
|
Vérification
|
n² + (1/2 (n² – 1))² |
= n² + 1/4 (n4 – 2n² +1) = 1/4 (n4 + 2n² +1) = 1/4 (n² + 1)² = (1/2 (n² + 1) )² |
|
|
Alternative
|
a b c |
= n = (a² – 1) / 2 = b + 1 |
|
|
Tous
|
k n 1/2 k (n² – 1) 1/2 k (n² + 1) |
= 3 x 5 = 15 =
3 x 12 = 36 =
3 x 13 = 39 |
|
Observation
|
|
|
|
|
|||
|
Méthode
NB:
tout nombre pair est générateur d'un triplet |
n (n/2)² – 1 (n/2)² +
1
|
=
4 =
4 – 1 = 3 =
4 + 1 = 5 |
|
|
Vérification
|
n² + ((n/2)² – 1)² |
= n² + (n/2)4 – 2(n/2)² + 1 =
(n/2)4 + 2(n/2)²
+ 1 = (n/2)² + 1 |
|
|
Alternative
|
a b c |
= n = (a/2)² – 1 = b + 2 |
|
|
|
k n k{ (n/2)²
– 1 } k{ (n/2)²
+ 1 } |
=
3 x 4 = 12 =
3 x 3 = 9 =
3 x 5 = 15 |
|
Observation
|
|
|
|
|
|||
|
Méthode
u
– v = 1 mod 2 (=>
u – v est impair). Autrement dit: l'un pair et
l'autre impair. pour
obtenir des triplets primitifs. |
u² – v² 2uv u² + v² |
= 4² – 3²
= 7 = 2 . 4 . 3 = 24 = 4² + 3²
= 25 |
|
|
Vérification La
somme des carrés donne bien le carré de l'hypoténuse. |
(u² – v²)² + (2uv)² |
= u4
– 2 u²v² + v4 – 4u²v² = u4 + 2u²v² + v4 = (u²
+ v²)2 |
|
|
Valeur de u, v Connaissant
le triplet retrouvez les deux nombres générateurs. |
|
|
|
Observation
|
|
|
|
sans imposer les restrictions sur u
et v |
|
|
|
Exemples u en => et v en |
|
|
|
Tous |
Dit-autrement,
avec ces formules, lorsque les triplets non primitifs sont exclus, alors
reste la liste de tous les triplets primitifs. Voir Exemples pour les
nombres de 1 à 500
|
|
|
Complexes |
(u + iv)² = (u² – v²) + i2uv |
|
|
D'où vient cette formule? |
|
||
|
Explications
|
b² (b/2)² |
= c² – a ² = (c – a) (c + a) = { (c –
a) / 2 } { (c + a) / 2 } |
|
|
|
b a c c - a c + a |
pair impair impair pair pair |
|
|
|
(c + a) /
2 (c – a) /
2 |
= u entier = v entier |
|
|
|
u v c = u + v a = u – v |
= x.d = y.d = x.d + y.d = x.d - y.d |
|
|
|
c a d |
= (x + y) . d = (x – y) . d = 1 |
|
|
Première conclusion
Seule
possibilité: pour donner un carré, le produit doit être un produit de carrés. |
(c + a)
/ 2 (c – a)
/ 2 PGCD(u, v) (b/2)² |
= u = v = 1 = { (c – a) / 2 } { (c + a) / 2 } = u . v = U² . V² |
|
|
Deuxième conclusion
|
U² V² U.V |
= (c + a)
/ 2 = (c – a)
/ 2 = b/2 |
|
|
|
a b c |
= U² – V² = 2 U.V = U² + V² |
|
|
|
||
|
Jumeaux par l'hypoténuse
Calculez ( u² – v², 2uv,
u² + v² ).
si
2uv et u² + v² le sont 2uv + 1 = u² + v² u² + v² - 2uv = 1 (u – v)² = 1 |u – v| = 1
|
u v
a b
c 2 1
3 4
5 3 2
5 12 13 4 3
7 24 25 5 4
9 40 14 6 5 11 60 61 Les
nombres c sont les nombres carrés
centrés: cn = (n + 1)² + n² et les
nombres b sont les nombres quadrillages,
ou quatre fois triangulaires:
bn = 4 Tn = 2 n (n
+ 1) |
|
|
Propriétés
|
(1, 3, 6, 10, 15, …
) x 4
|
|
|
Note a²
+ (a + 1)² = 2a² + 2a + 1 = 2a (a + 1) + 1 = c² La
somme des carrés de deux nombres consécutifs est égale à deux fois leur
produit plus 1. Ex: 20² + 21²
= 2 x 20 x 21 + 1 = 841 = 29² |
a b c 3 4 5 21 20 29 119 120 169 697 696 985 4059 4060
5741 |
|
|
|
||
|
Méthode 1 – triviale
|
3, 4, 5 => 6,
8, 10 9,
12, 15 … |
|
|
Méthode 2 – performante
|
||
|
|
|||
|
Méthode
|
n n – 1 n + 1 |
=
8 =
7 =
9 |
|
|
|
1/(n–1) + 1/(n+1) =
|
=
1/7 + 1/9 =
16/63 =
M/N |
|
|
|
M N O |
=
16 =
63 =
65 |
|
|
Explications
|
u v |
= u = 1 |
|
|
|
M N O |
= 2u = u² – 1 = u² + 1 |
|
|
|
||
|
Quadruplets …
|
3² + 4² = 5² 5² +
12² = 13² 3² + 4²
+ 12² = 13² |
|
|
|
13² + 84² = 85² 3² + 4²
+ 12² + 84² = 85² |
|
|
Généralisation
Le
nombre étant toujours impair, on
utilise la formule du plus 1
|
3² + 4² = 5² 5² +
12² = 13² 3² + 4²
+ 12² = 13² 13² + 84² = 85² 3² + 4²
+ 12² + 84² = 85²
85² + 3612² = 3613² 3² + 4²
+ 12² + 84² + 3612² = 3613² Etc. 8² + 15² = 17² 17²
+ 144² = 145² 8² + 15² + 144² = 145² 145² +
10512² = 10513² 8² + 15² + 144² + 10512² = 10513² Etc. |
|
|
|
||
|
Triplets à la
puissance 3 et plus
C'est
le théorème de Fermat -Wiles. |
xn + yn |
|
|
Quadruplets à la
puissance 3 et plus
|
33 + 43
+ 53 = 63
>>> 13 + 63
+ 83 = 93
>>> 33 + 103
+ 183 = 193 73 + 143
+ 173 = 203 >>> 43 + 173
+ 223 = 253 183 + 193
+ 213 = 283 113 + 153
+ 273 = 293 |
|
|
|
95 8004 + 217 5194 + 414 5604
= 422 4814 >>> 2 682 4404
+ 15 365 6394 + 18 796 7604 = 20 615 6734 |
|
|
k-uplets à la
puissance n
Puissance
ou pas. C'est
le théorème de Waring. |
Tout nombre est décomposable en somme de 4
carrés; a fortiori tout carré. Tout nombre est décomposable en somme de 9
cubes; a fortiori tout cube. Etc. |
|
Retour à Somme
de puissances
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/TripGene.htm |
![]()