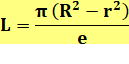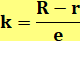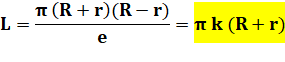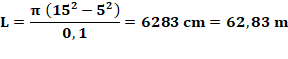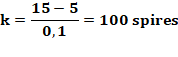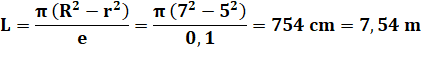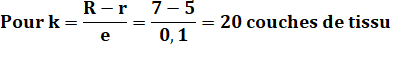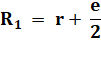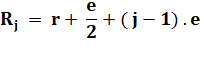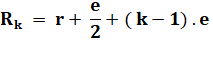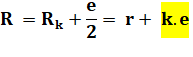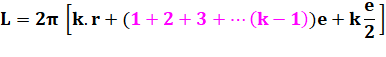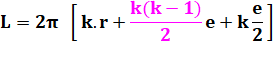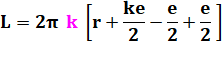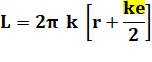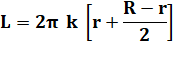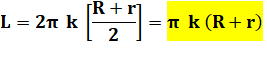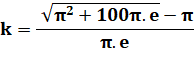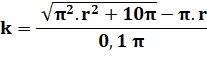|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
BOBINE – ROULEAU Longueur et quantité de spires Comment calculer la longueur
d'un tapis enroulé sur son mandrin; d'une bande de papier sur sa bobine, d'un
feuillard sur son dévidoir; d'une bande de matériau quelconque sur son
bobineau; etc. La clé du calcul
|
Anglais: how to calculate rolled length of roll material?
Thickness of material /
Diameter of center hole / Area of cross-section /
Radius of the layer, of the wrap
|
|
||
|
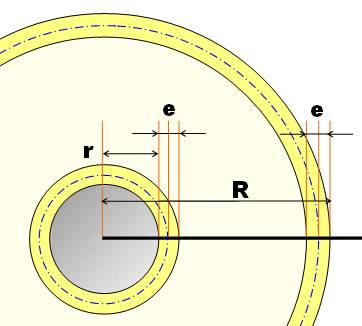
Problème Connaissant
les trois paramètres indiqués (R, r et e), quelle est la longueur de la
feuille de tôle? Calcul de la longueur L On
compare deux surfaces:
S = L . e
Ces deux
surfaces sont égales et la longueur est donnée par:
Quantité de spires k (de couches)
Relation entre L et k
|
Notations
Exemple numérique Avec R = 15 cm,
r = 5 cm et e = 0,1 cm
Sensibilité à la mesure de l'épaisseur Avec e = 0,09 cm, L = 69,81 m Avec e = 0,10 cm, L = 62,83 m Avec e = 0,11 cm, L = 57,12 m |
|
Calcul pratique
|
Mon
rouleau de tissu entamé fait 14 cm de diamètre sur un mandrin de 10 cm de diamètre.
Mon étoffe mesure 1/10 cm d'épaisseur. Quelle est la longueur d'étoffe qui me
reste?
|
|
|
|||
|
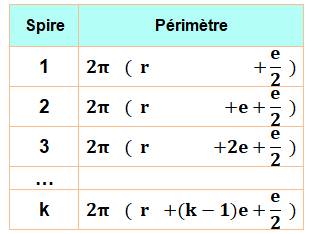
Prise en compte de la taille des
spires On étudie
l'influence de la taille des spires, plus courtes vers le centre et plus
longue en périphérie. On va vérifier que le calcul précédent était tout à fait valide, malgré
la variation de longueur des spires. On
calcule le périmètre moyen d'une spire en utilisant le rayon moyen soit r +
e/2 pour la première spire. Longueur des spires selon leur rang
|
Rayon moyenn d'une spire:
|
||
|
Longueur de la feuille C'est la somme des longueurs de toutes les
spires. Voir le calcul de la somme des
entiers. Le produit k.e est l'épaisseur de toutes les
spires et vaut la différence de diamètre. Note Le calcul pourrait être repris en encadrant
l'estimation de L, ceci en calculant
avec le bord inférieur et le bord supérieur de chaque spire. |
|
||
|
|
||
|
Évaluation
de l'aire de la couronne (section) de chaque spire. La somme
des sections des spires est égale à la section de la bande déroulée. On
retrouve, à nouveau, notre formule. |
|
|
|
|
||
|
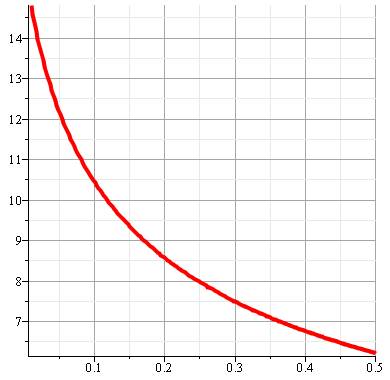
Problème Comment
varie la quantité de spires (de couches) lorsque l'épaisseur ou la taille du
mandrin décroit, avec une longueur de tissu, de papier ou de tôle constante. |
|
|
|
Résolution pour k = f (e) Avec L = 100 cm et r = 1 cm La racine positive de cette équation du second degré donne k en
fonction de e. Une hyperbole
avec l'axe des y en asymptote. Dit-autrement: plus le matériau est fin et plus
il y aura de tours autour de la bobine pour une longueur donné (évident) Ce nombre de tours tend vers l'infini pour e
tendant vers zéro, quelle que doit la taille de la bobine. Vérification Avec 10 tours, R = 1 + 0,1 x 10 = 2 et |
|
|
|
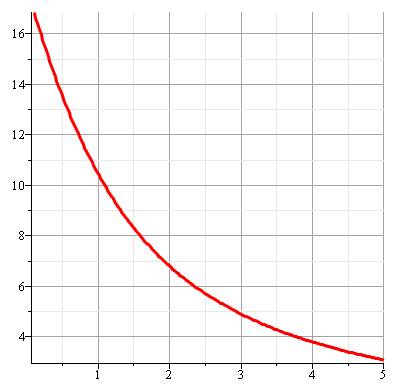
Résolution pour k = f (r) Avec L = 100 cm et e = 0.1 cm Même tendance avec un rayon de la bobine qui
décroit. Si le rayon tend vers 0, la quantité de couches tend
vers l'infini. Note: à longueur
constante de matériau, en faisant
décroitre le rayon et l'épaisseur, chacun vers 0, la quantité de couches
tend, bien entendu, vers l'infini … plus vite. Note sur la construction des
courbes Sur le graphe du bas, avec le millième de
centimètre d'épaisseur, on arrive à plus de 15 000 tours autour de la bobine. |
|
|
|
Les
formules de calcul sont finalement assez simples. Mais attention à la
sensibilité à la précision de mesure, surtout pour l'épaisseur e. Pour
les matériaux compressibles comme les tissus ou les tapis, mieux vaut
étalonner en mesurant, au moins une fois, la longueur de la bande d'étoffe et
en déduire l'épaisseur. |
![]()
|
|
||
|
On se pose la question de savoir ce que devient
le diamètre de la bobine en cas d'une
épaisseur de ruban qui tend vers 0. |
Bobine: diamètre: D = 1 cm circonférence:
C = 3,14 cm Ruban: longueur: L = 3,14 m épaisseur: E = 0,1 mm |
|
|
Première situation – Épaisseur
variable La seule chose qui va varier, c'est le diamètre
de la bobine remplie (Dr). Son diamètre sera égal à D + 2 x 100 x E. Si E tend vers zéro, Dr tend vers D. |
k = L / C = 314 / 3,14 = 100 tours La quantité de tours k ne dépend pas de
l'épaisseur, pour une épaisseur restant très petite et tendant vers 0. Si l'épaisseur tend vers 0, k reste égal à 100. |
|
|
Deuxième situation: effet de
laminage Lorsque l'épaisseur est divisée par 10, la
longueur du ruban est multipliée par 10 par effet de laminage,
c'est à dire: conservation de la même quantité étoffe (conservation du même
volume de matière). Le diamètre de la bobine reste celui calculé plus
haut, car on a la même quantité de matière. |
Avec D = 1cm et, e/10, L = 31,4 m => k = 3140/3,14 = 1000
tours e/100, L = 314 m =>k = 31400/3,14 = 10 000 e/infini, L = 31400...0 m => k =
31400...0/3,14 = quantité infinie de tours Avec L x e = constante, si e tend vers zéro, L
tend vers l'infini, et également la quantité k de tours. |
|
|
Troisième cas: limite mathématique
(théorique) Ce qu'il faut comprendre: la ligne est un objet mathématique
qui n'a pas d'épaisseur; c'est un objet à une seule dimension. |
Même si je trace un million de lignes l'une sur
l'autre, ça restera une ligne sans épaisseur; ou d'épaisseur nulle, si vous
voulez. Enroulée sur la bobine, une demi-droite, crée le
même effet. Il n'y a pas création d'épaisseur puisque qu'elle est nulle. |
|
|
Conclusion si e tend vers 0 En mathématique: le diamètre de
la bobine remplie est toujours celui de la bobine vide |
En physique: le diamètre de
la bobine remplie est plus grand que celui de la bobine vide. Il tend vers
celui de la bobine vide pour une épaisseur qui tend vers 0. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()
-