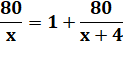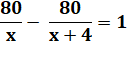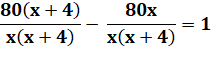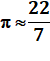NOMBRES – Curiosités, Théorie et Usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 03/07/2021

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths                                                                              

Algèbre

 

Débutants

Équations

ÉQUATIONS

du 2e degré

 

Glossaire

Équations

2e degré

 

 

INDEX

Équations

 

Introduction

Résolution graphique

Solutions entières

Somme et produit

Résolution simple

Nombres

Historique

Résolution générale

Applications

 

Sommaire de cette page

>>> Livres

>>> Âges du père et du fils

>>> Âge de Clément

>>> Encore père et fils

>>> Train

>>> Robinet

>>> Triangle

>>> Rectangle

>>> Cylindre

 

 

 

 

ÉQUATIONS du 2e degré

 Utilisation pratique

 

Exemples de problèmes concrets résolus.

 

 

 

Les LIVRES

 

Problème

Le libraire achète des livres pour 80 €.

Avec 4 livres de plus, pour le même prix total, chaque livre aurait coûté 1€ de moins.

 

Illustration

 

 

Solution

Réalité

Supposition

*      La quantité de livres:

x

x + 4

*      Coût de chaque livre:

80 / x

80 / (x + 4)

*      Traduction de l'énoncé

Les coûts diffèrent de 1 euro:

80 / x =

1 + 80 / (x + 4)

*      Expression et mise en dénominateur commun.

 

 

 

*      Calcul avec produits en croix.

80 (x + 4) – 80x  = x (x + 4)

80x + 320 – 80x = x² + 4x

320 = x² + 4x

x² + 4x – 320 = 0

*      Discriminant:

b² – 4ac

= 16 – 4 . 1 . (–320)

= 16 + 1 280

= 1296

= 36²

*      Racines:
La solution négative est à rejeter.

x1 = (–4 + 36) / 2 =   16

x2 = (–4 – 36) / 2 = –20

*      Nombre de livres et

Prix de chaque livre:

16 livres à 80/16 = 5 €

En effet:

16 x 5 = 80

20 x 4 = 80

 

 

Âge du père et âge du fils

 

Problème

Il y a tout juste 1 an, un homme avait 8 fois l'âge de son fils.

Aujourd'hui son âge est le carré de celui de son fils.

Trouvez son âge.

 

Solution

 

Il y a un an

Aujourd'hui

*      Âge du fils:

x

x + 1

*      Âge du père:

8x

8x + 1

*      Traduction de l'énoncé:

(âge fils)²  =  âge du père, aujourd'hui

(x + 1)² = 8x + 1

x² + 2x + 1 = 8x + 1

x² –  6x  = 0

x(x – 6) = 0

*      Racines:
La solution nulle est à rejeter.

x1 = 0

x2 = 6

*      Âge du fils et

Âge du père:

6 + 1       =   7 ans

8 x 6 + 1 = 49 ans

Voir  Problème sur les âges / Âges devinés

 

 

Âge de Clément

 

Problème

Le produit de l'âge de Clément dans 10 ans par celui qu'il avait il y a 10 ans est égal à 44.

Quel est l'âge de Clément ?

 

Solution

 

Il y a 10 ans

Dans 10 ans

*      Âge de Clément:

x

x + 20

*      Traduction de l'énoncé:

x (x + 20) = 44

x² + 20x – 44 = 0

*      Calcul (factorisation):

x² + 22x – 2x – 44 = 0

x(x + 22)  – 2(x + 22) = 0

(x – 2) (x + 22) = 0

*      Racines:
La solution négative est à rejeter.

x1 =     2

x2 = –22

*      Âge de Clément il y a 10 ans et âge actuel:

2 ans

2 + 10 = 12 ans

Voir Brève 670

 

 

 

Encore père et fils

 

Problème

Dans 6 ans le père aura 3 fois l'âge de son fils.

Il y a 3 ans, il était 9 fois plus âgé que son fils.
 

Solution

 

Il y a 3 ans

Dans 6 ans

(9 ans plus tard)

*      Âge du père

Âge du fils

9x

x

9x + 9

  x + 9

*      Traduction de l'énoncé

3 (x + 9) = 9x + 9

3x + 27  = 9x + 9

6x = 18

*      Racines
Second degré inutile!

x = 18/6 = 3

*      Âge du fils il y a 3 ans

Âge actuel

Âge du père

3 ans

3 + 3 = 6 ans

9 x 3 + 3 = 30 ans

 

 

Le TRAIN

 

Problème

Avec 5 km/h de plus le train mettrait 2 heures de moins sur un trajet de 300 km.  Quelle est sa vitesse?

 

Rappel fondamental

Dans tout problème de vitesse on se souvient de la formule qui servira toujours: Longueur = vitesse multipliée par le temps (durée):

 

L =  v . T

 

Solution

Normal

Fictif

*      Vitesse:

v

v + 5

*      Trajet:

L = 300

L = 300

*      Durée:

TN = 300 / v

TF = 300 / (v + 5)

*      Traduction de l'énoncé:

TN – 2 = TF

300 / v – 2 = 300 / (v + 5)

(300 – 2v ) / v = 300 / (v + 5)

(300 – 2v ) (v + 5) = 300v

300v – 2v² + 1 500 – 10v = 300v

2v² + 10v – 1 500 = 0

v² + 5v – 750 = 0

*      Discriminant

b² – 4ac

= 5² – 4 . 1 . (–750)

= 25 + 3000

= 3025

= 55²

*      Racines:

La solution négative est à rejeter.

x1 = (–5 + 55) / 2 =  25

x2 = (–5 – 55) / 2 = –30

*      Vitesse du train:

25 km/h

Voir Autres problèmes de trains

 

 

 

ROBINETS

 

Problème

On dispose de trois tuyaux de débit constant pour remplir la piscine.

Avec les 2 premiers utilisés simultanément, il faut le même temps

que pour la remplir avec le 3e seul.

Le 2e la remplit en 5 heures de moins que le premier et en 4 de plus que le 3e

Quelle est la durée de remplissage pour chaque tuyau seul ?

 

Rappel fondamental

Dans tout problème de robinet on se souvient de la formule qui servira toujours, analogue à celle de la vitesse: Volume = débit par temps (durée)

 

V =  d . T

 

Solution

Premier

Deuxième

*      Volume à remplir:

V

V

*      Durée de remplissage:

x + 5

x

*      Débit:

V / (x + 5)

V / x

*      Traduction de l'énoncé:

 

Débit du 3
     = débits du 1 et du 2

V / (x + 5) + V / x = V / (x – 4)

1 / (x + 5) + 1 / x = 1 / (x – 4)

x(x – 4) + (x + 5) (x – 4) = (x + 5) x

x² – 4x + x² + 5x –4x – 20 = x² + 5x

x² – 8x – 20 = 0

*      Discriminant:

b² – 4ac

= 8² – 4. 1 . (–20)

= 64 + 80

= 144

= 12²

*      Racines:

La solution négative est à rejeter.

x1 = (8 + 12) / 2 = 10

x2 = (8 – 12) / 2 = –2

*      Durée de remplissage
Avec 2

Avec 1

Avec 3

10 heures

10 + 5 = 15 h

10 – 4 =   6 h

Voir Robinets

 

 

TRIANGLE

 

Problème

Les longueurs des côtés de ce triangle rectangle sont des nombres consécutifs. Valeurs ?

 

Rappel fondamental

Le Théorème de Pythagore

 

a² + b² = c²

 

Solution

*      Longueur des côtés:

x - 1

x

x + 1 Hypoténuse

*      Traduction de l'énoncé:

(x + 1) ² = x² + (x – 1)²

x² + 2x + 1 = x² + x² – 2x + 1

x² – 4x = 0

*      Racines:

La solution nulle est à rejeter.

x1 = 0

x2 = 4

*      Longueur des côtés:

3

4

5                   En effet:    3² + 4² = 5²

 

 

RECTANGLE

 

Problème

Un rectangle de 308 m² dont la longueur mesure 8 mètres de plus que la largeur. Quelles sont les dimensions de ce rectangle?
 

Rappel

Aire du rectangle: A  = L x l (longueur par largeur)

 

Solution

*      Largueur:

Longueur:

Aire:

x

x + 8

x (x + 8)

*      Traduction de l'énoncé:

x (x + 8) = 308

x² + 8x – 308 = 0

*      Discriminant:

b² – 4ac

= 64 – 4 . 1 . (–308)

= 64 + 1 232

= 1 296

= 36²

*      Racines:

La solution négative est à rejeter.

x1 = (–8 + 36) / 2 = 14

x2 = (–8 – 36) / 2 = –22

*      Largeur:

Longueur:

14 m

14 + 8 = 22 m

 

 

CYLINDRE

 

Problème

Un cylindre dont l'aire totale est de 88 cm². Sa hauteur est égale à 5 cm.

Quel est le rayon du cylindre ?
 

Rappel

Aire totale du cylindre = aire de la surface courbe + aire des deux disques fermant le cylindre.

 

S = 2 r . h + 2 r²

 

Solution

*      Traduction de l'énoncé:

88 = 2r. 5 + 2r²

 

*      Remplaçons Pi par une valeur approchée:

*      L'équation devient:

88 = 2 .22 . r² / 7 + 2 . 22 .r. 5 / 7

7 x 88 = 44 r² + 220 r

7 x 2 = r² + 5 r

r² + 5r – 14 = 0

*      Résolution (factorisation):

(r + 7) (r – 2) = 0

*      Racines:

La solution négative est à rejeter.

r1 = –7

r2 =   2

*      Rayon du cylindre

r = 2 cm

 

 

 

 

Suite

*    Autre cas concret: le loueur de vélos

*    Voir haut de page

Voir

*    Algorithme d'Héron

*    Équations en poèmes

*    Géométrie – Index

*    Méthode de Newton

*    Système d'équations – Somme100

Cette page

*    http://villemin.gerard.free.fr/ThNbDemo/Eqa2dApl.htm