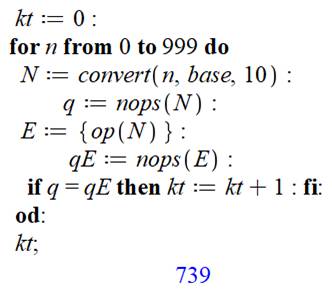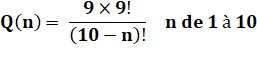|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
ARRANGEMENTS avec les NOMBRES Compter les chiffres pour former les nombres. Combien de 9 pour
paginer un livre de 100 pages? Les dix 9 pour les unités auquel il faut ajouter
les dix 9 pour les dizaines de quatre-vingt-dix. Soit 20 fois le chiffre 9. Combien de chiffres
pour paginer ce livre? Il faut 9 chiffres pour les unités; 9 x 10 x 2 = 180
chiffres pour les nombres de 10 à 99 et 3 chiffres pour la page 100. Total: 9
+ 180 + 3 = 192. |
Voir Calculer la quantité de chiffres
dans un nombre
|
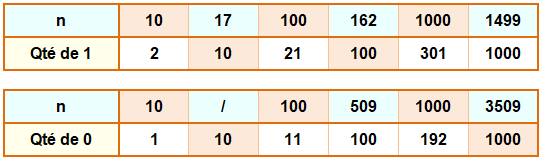
Exemples Il
y a 21 fois le chiffre
1 pour écrire tous les nombres de 1
à 100. Un
livre de 162 pages utilise 100 fois le chiffre 1 pour sa pagination. Un livre de 333 pages comptera 102
fois le nombre 3. Il faut atteindre la page 509 pour avoir utilisé cent fois
le 0. |
|
Voir Brève
636
Somme des quantités de chiffres des nombres jusqu'à n
|
Exemple 1,
2, 3, 4, 5, 6, 7, 8, 9 10 => 11 chiffres Année
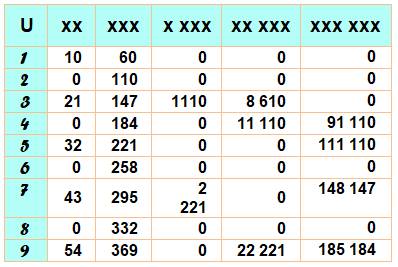
2019 La quantité des chiffres formant tous les nombres de 1 à 2019 est égale à 6969. Curiosités 1, 2, 3, …, 65, 66 => 123 1, 2, 3, …, 3
363 => 12 345 1, 2, 3, …, 143
=> 321 1, 2, 3, …, 1
357 => 4 321 Avec les
repdigits Ex: 1, 2, 3, …, 258
=> 666 (= 6 dans XXX)
|
|
|
|
|
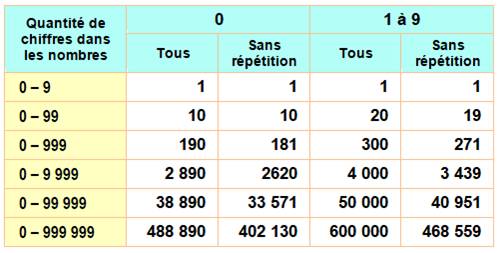
Quantité de chiffres dans les nombres de 0 à
99…9:
Lecture:
pour écrire les nombres de 0 à 999, il faut
190 fois le chiffre 0 et 300 fois chacun des autres chiffres de 1 à 9. Il
faut 181 nombres contenant au moins un 0 et 271 nombres contenant au moins un
1 ou un des autres chiffres. Voir calcul détaillé >>> Quantité de nombres inférieurs à une valeur
donnée:
Lecture:
Il faut écrire 100 nombres pour noter tous
les nombres de 0 à 99 (évident!). Il n'en reste que
91, si on élimine tous les nombres où deux chiffres, ou plus, qui se
répètent. De 101 à 999, ils sont 648 de plus, soit un total de 739 (74%). De 0 à 999 999,
il y a 168 571 nombres avec des
chiffres différents (17%). De 0 à 9 999 999,
il y ena 712 891 (7%). Voir calcul détaillé >>>
|
|
|
|
Ce
programme compte la quantité de nombres ayant des chiffres différents (kt). Voir tableau juste ci-dessus. La
boucle analyse tous les nombres de 0 à
999. Chacun
est converti en base 10 qui, en fait, donne la liste des chiffres. La quantité de ces
chiffres est mise en q. Cette
liste est transformée en ensemble,
opération qui supprime les doublons dans la liste. La quantité de chiffres
restante est mise en qE. Si
les deux quantités (q et qE) sont égales, c'est que les chiffres étaient bien
différents. Si
c'est le cas, le compteur est incrémenté. Après
la fin de boucle (od), on demande l'affichage de kt. Ici,
le programme affiche 739 nombres différents parmi les nombres de 0 à 999. |
Voir Programmation
– Index
|
|
|||
|
Nombres
comportant un seul 5. |
9 possibilités pour x (de 0 à 9, sans le 5) 9 possibilités pour y 9 possibilités pour z |
9 x 9 x 9 x 3 = 243 |
|
|
Nombres
comportant deux 5. |
9 possibilités pour chaque |
9 x 3 = 27 |
|
|
Nombres
comportant trois 5. |
1 possibilité |
= 1 |
|
|
Total |
Les cas analysés sont disjoints, les quantités s'ajoutent |
271 |
|
|
Sur le
même principe de calcul |
Combien de 55 de 0 à 999 x55, 5x5 et 55 |
9 x 3 = 27 |
|
Note: la notation des nombres manquants en
x et y est pratique à condition de se souvenir que ces deux nombres sont
interchangeables. |
Combien de 55 de 0 à 9 999 xy55, x5y5, x55y, 55xy,
5x5y,5xy5 |
9x9 x 6 = 486 |
|
On aurait pu mettre un point pour représenter un nombre
et trouver 10 configurations possibles. C'est aussi 3 parmi 5 = (5x4x2) / (3x2x1)
= 10. |
Combien de 55 de 0 à 99 999
|
9x9x9 x 10 = 7 290 |
|
|
||||||
|
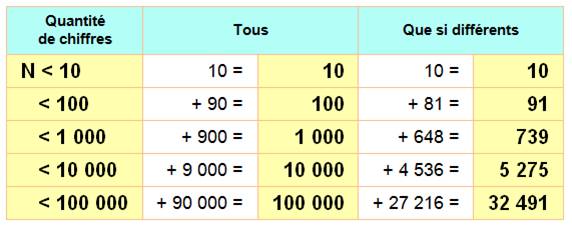
Le dénombrement est très évident: - Le calcul direct
est donné en bas de tableau. - Le calcul pas à pas
permet de tracer la méthode pour le cas où les chiffres sont différents. |
||||||
|
Contrainte |
Résultats |
Illustration En rouge les interdits |
||||
|
1
chiffre |
Il
y a évidemment 10 possibilités. |
u = {0, 1,
2, 3, 4, 5, 6, 7, 8, 9} => 10 |
||||
|
2
chiffres |
Calcul
pour chaque position des chiffres: -
L'unité
peut prendre l'une des 10 valeurs des chiffres; et -
La dizaine
peut être l'un quelconque des 9 chiffres (0 exclu, en tête d'un nombre). Total:
principe multiplicatif 10
x 9 = 90 |
u = {0, …
9} => 10 d = {0, 1, … 9}
=> 9 |
||||
|
3
chiffres |
Calcul
pour chaque position des chiffres: -
L'unité
peut prendre l'une des 10 valeurs des chiffres; -
La dizaine
peut être l'un quelconque des 10 chiffres (0 y compris); et -
La centaine
peut être l'un quelconque des 9 chiffres (0 exclu, en tête d'un nombre). Total:
principe multiplicatif 10
x 10 x 9 = 900 |
u = {0, … 9} => 10 d = {0, … 9} => 10 c = {0, 1, … 9} => 9 |
||||
|
TOTAL N
< 1000 |
C'est
le total des calculs précédents -
1 chiffre:
10 -
2 chiffres
: 90 -
3
chiffres: 900 Total
de nombres inférieurs à 1000 divisibles par 2 10
+ 90 + 900 = 1000 |
Résultat sans
surprise: il y a bien 1000 nombres entre 0 et 999 compris. |
||||
|
Calcul direct |
On
considère les nombres à 3 chiffres, même s'ils commencent par des 0. On y
trouvera également les cas 000 qui vaut 0 ou 010 qui vaut 10, etc. Total: 10 x 10 x 10 = 1000 |
u = {0, …
9} => 10 d = {0, …
9} => 10 c = {0, … 9} => 10 |
||||
|
|
|||||||
|
On se propose de
dénombrer les nombres ayant des chiffres tous différents. |
|||||||
|
Contrainte |
Résultats |
Illustration En rouge les interdits |
|||||
|
1 chiffre |
On
retrouve les 10 possibilités: 10 |
|
|||||
|
2 chiffres différents 11 22 … exclu |
Calcul
par position des chiffres: -
Dizaine:
toutes les possibilités, de 1 à 9, soit 9 -
Unité:
toutes les possibilités sauf le chiffre déjà choisi pour les unités, soit 9. Total:
principe multiplicatif: 9
x 9 = 81 |
d = {0, 1, … 9}
=> 9 u = {0, …d … 9} => 9 |
|||||
|
|
Notez
que l'on examine les dizaines avant les unités du fait du rôle non symétrique du 0 Si on
avait pris les unités en premier on aurait trouvé 10 x 8 = 80 et non pas 81 -
En fait le
zéro n'est pas autorisé en tête de nombre; -
Alors
qu'il l'est pour les unités. |
FAUX
u = {0, 1, … 9} => 10 d = {0, …d … 9} => 8 |
|||||
|
3 chiffres tous différents 100 101 110 … exclus |
Calcul
par position des chiffres: -
Centaine: toutes
les possibilités, de 1 à 9, soit 9; -
Dizaine:
toutes les possibilités sauf le chiffre déjà choisi pour les unités; et -
Unités:
toutes les possibilités sauf les deux chiffres déjà choisis pour les unités
et les dizaines. Total:
principe multiplicatif 9
x 9 x 8 = 648 |
c = {0, 1, … 9} => 9 d = {0, 1, … c … 9}
=> 9 u = {0, 1 ..c ..d … 9} => 8 |
|||||
|
4 chiffres tous différents |
Avec
le même principe, on trouve: Total:
principe multiplicatif 9
x 9 x 8 x 7 = 4 536 |
m = {0, 1, … 9} => 9 c = {0, 1, … m … 9}
=> 9 d = {0, 1, .. m ..c … 9}
=> 8 u = {0, 1, … m .. c.. d
… 9} => 7 |
|||||
|
TOTAL < 10 000 avec des chiffres
différents |
Total
de nombres inférieurs à 10 000 ayant des chiffres différents 10 + 81 + 648 + 4
536 = 5 275 |
|
|||||
|
Liste Q(n) |
9
ou 10, 81, 648, 4536, 27216, 136080, 544320, 1632960, 3265920, 3265920. |
OEIS A073531 – Number of n-digit positive
integers with all digits distinct |
|||||
|
Formule |
|
La liste
des Q(n) est finie. |
|||||
|
|
|||||||||||
|
Contrainte |
Résultats |
Illustration |
|||||||||
|
En employant les arrangements |
Quantité
d'arrangements de tous les nombres de 4 chiffres: A410
= 10 x 9 x 8 x 7 = 5 040 Il
faut supprimer tous ceux commençant par 0. Quantité
d'arrangements de tous nombres de 3 chiffres (le 0 étant positionné, on
cherche les arrangements sur c d u) A39 = 9 x 8 x 7 = 504 Bilan 50 40 – 504 = 4 536 |
|
|||||||||
|
Méthode la plus simple |
Le
chiffre des milliers est l'un des chiffres sauf le 0: 9 possibilités. Les
trois autres chiffres sont les arrangements de tous les chiffres, y compris
le 0, sauf celui déjà utilisé pour les milliers: soit
9 possibilités pour 3 positions Total 9 x A39
= 9 x 9 x 8 x 7 = 4 536 |
|
|||||||||
|
Généralisation |
Calculer
la quantité de nombres différents à n chiffres pour les nombres inférieurs à
10n: 9 x An-19
= 9 x 9 x 8 x … x (11 – n) = 9 x 9! / (10 – n)! |
|
|||||||||
|
Limite |
Évidemment
avec un nombre à 11 chiffres, il est impossible d'avoir des chiffres tous
différents. À
noter que, pour passer de 9 chiffres à 10 chiffres, le nombre et imposé. On
n'ajoute pas de nombres supplémentaires. |
Nombre à
10 chiffres 9 x 9! = 3 265 920 |
|||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Soit
la règle: Delta = Delta précédent
x chiffres décroissants |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()