NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/11/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	DROITES
Débutants Géométrie	Passant par k points					Glossaire Géométrie
INDEX GÉOMÉTRIE Dénombrement	Droites par n points		Diagonales polygones	Segments dans les objets
	Segments dans grille		Grille: droites par 2 points	Grille: droites par 3 points
	Obliques dans une grille
		Sommaire de cette page >>> Grilles 3x3 et 4x4 >>> Grilles 5x5 et 6x6 >>> Table des valeurs >>> Grille 8 x 8 à 3 points exactement

Quantité de droites

passant par trois points

sur une grille k x k

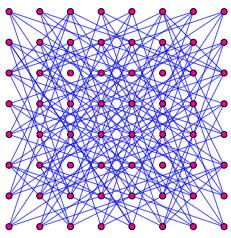
Une grille régulière de points. Combien peut-on dessiner de droites passant par trois points? Soit trois points exactement ou trois points ou plus.

Illustration: grille 8x8 avec ses 100 droites

passant par 3 points exactement

Approche: Grilles 3x3 et 4x4
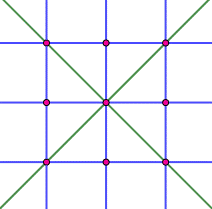
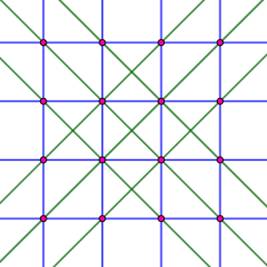
Une grille régulière de points ordonnés selon une matrice (k, k). Cas (3, 3) Bleu: 2 x 3 droites horizontales et verticales. Vert: 2 x 1 droites obliques. Total: 8 droites, toutes passent par exactement 3 points. Cas (4, 4) Bleu: 2 x 4 droites horizontales et verticales. Vert: 2 x 3 droites obliques. Total: 14 droites dont 4 seulement passent par 3 points exactement.

Grilles 5x5 et 6x6
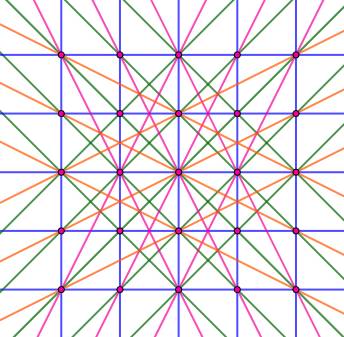
Cas (5, 5) Bleu: 2 x 5 droites horizontales et verticales. Vert: 2 x 5 droites obliques avec pente (1, 1) Rouge: 4 x 3 droites obliques avec pente (2, 1) Total: 32 droites dont 16 seulement passent par 3 points exactement.
Cas (6,6) Bleu: 2 x 6 droites horizontales et verticales. Vert: 2 x 7 droites obliques avec pente (1, 1) Rouge: 4 x 8 droites obliques avec pente (2, 1) Total: 58 droites dont 36 seulement passent par 3 points exactement.

Quantité de droites passant par trois points
3 points exactement	0, 0, 0, 8, 4, 16, 36, 64, 100, 204, 252, 396, 572, 780, 1020, 1484, 1756, 2260, 2828, 3540, 4332, 5556, 6372, 7716, 9188, 10684, 12292, 14684, 16588, 19324, 22268, 25420, 28780, 33164, 36452, 41036, 45892, 51324, 57060, 64540, 70500, 77724, 85300, 93228, …
3 points ou plus	0, 0, 0, 8, 14, 32, 58, 108, 174, 296, 406, 628, 898, 1216, 1582, 2188, 2754, 3528, 4398, 5524, 6778, 8336, 9778, 11812, 14038, 16456, 19066, 22540, 25954, 29968, 34270, 39116, 44282, 50312, 56026, 63196, 70798, 78984, …

DicoNombre: 16 / 32 / 36 / 58 / 100

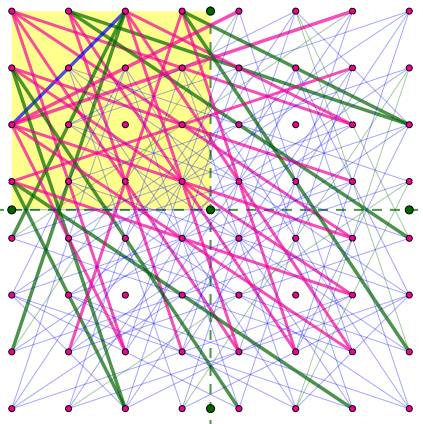
Grille 8 x 8 à 3 points exactement – 100 droites (ici, limitées aux segments)

Dénombrement

Sur cette grille, il se trouve que tous les segments passant par trois points exactement ont un bord pour sommet. Il suffit de compter les segments au départ des points de bordure d'un quadrant (traits épais): 1 segment interne (bleu), 18 qui s'arrêtent dans le dessin (roses), 12 qui rejoignent un autre bord (verts). Les deux premières catégories se retrouvent 4 fois dans la figure complète. Les 12 sont à compter dans le premier quadrant, ils ne seront plus que 8 dans le suivant, puis 4 et 0 ensuite. Bilan: 4 (1 + 18) + 12 + 8 + 4 = 100 droites par 3 points exactement. Par trois ou plus, il y en a 174.

Voir Brève 532

Suite	Quantité de droites par deux points Quantité de carrés dans le quadrillage d'un rectangle Constructions élémentaires: rectangle Le terrain de basket Losange Pavage avec des rectangles Quadrilatères – Juniors
Voir	Allumettes en carrés Allumettes et quadrillage Carré Construction à la règle et au compas Dénombrer – Index DicoMot Maths Énigmes classiques Ensembles – les compter Géométrie Pentominos Jeux – Index
Sites	A018810 - Number of lines through exactly 3 points of an n X n grid of points A225606 - Number of distinct lines passing through 3 or more points in an n X n grid A119437 - Table T(n,k) = number of lines through exactly k points of an n X n grid of points On lines and their intersection points in a rectangular grid of points – Seppo Mustonen – Référence sur ce sujet qui note quelques erreurs sur les pages indiquées ci-dessus. On lines through a given number of points in a rectangular grid of points – Seppo Mustonen Some formulas for numbers of line segments and lines in a rectangular grid - Pentti Haukkanen and Jorma K. Merikoski - Niveau supérieur.
Cette page	http://villemin.gerard.free.fr/GeomLAV/Carre/SegGril3.htm