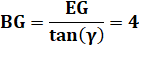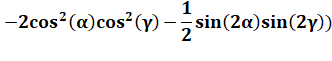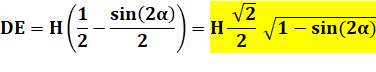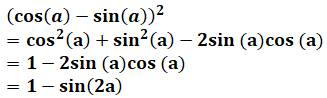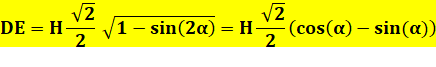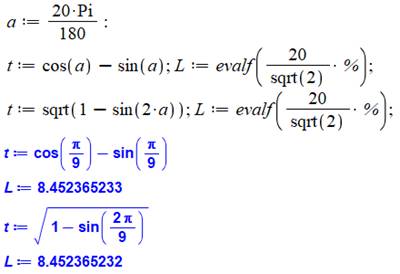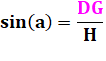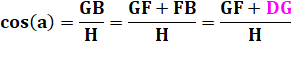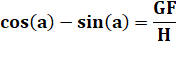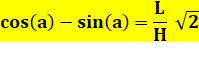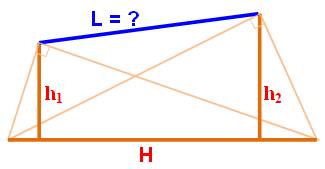
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/09/2020 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	TRIANGLES
Débutants Triangle	Résolution				Glossaire Triangle
INDEX Triangle	Résolution	Formules	Hauteur	Aire (Héron)
	Hypoténuse	Longueur de corde	Projection	T 13 14 15
	Triangle Rectangle – Cas classiques		Triangle Rectangle – Cas spéciaux
		Sommaire de cette page >>> Approche >>> Calcul avec les angles en B >>> Calcul avec les hauteurs >>> Calcul du triangle rectangle isocèle >>> Simplification de la relation >>> Retrouver la formule par construction

TRIANGLES RECTANGLES

Longueur d'une corde entre deux triangles rectangles

Deux triangles rectangles de même hypoténuse (H). On relie les sommets de l'ange droit de chacun.

Quelle est la longueur (L) de ce segment ?

L'hypoténuse est le diamètre d'un cercle et L est une corde du cercle.

Deux cas généraux

On connait (H) et un des angles de chacun des triangles, calculez L.

On connait (H, h₁, h₂), calculez L.

Un cas particulier

La hauteur h₂ est un axe de symétrie du segment H. Comment calculer L à partir du cas général ?

Idem, comment calculer simplement L avec une construction astucieuse ?

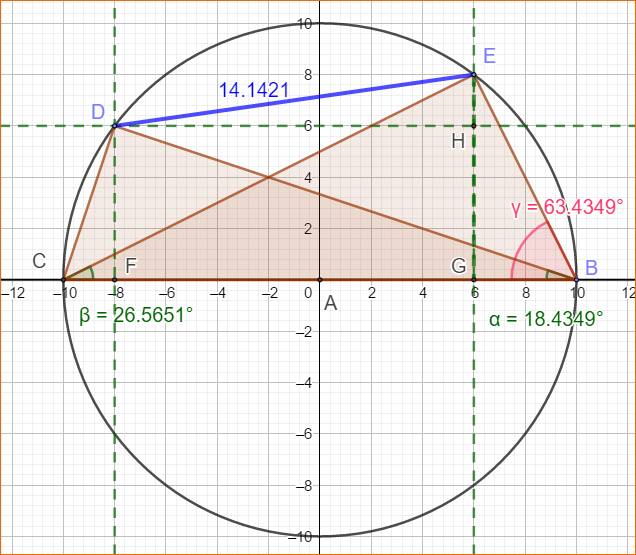
Figure pour notations et exemple numérique

Approche
Deux triangles rectangles CBE et CDB.	La corde DE
Avec le théorème de Pythagore:	DE² = DH² + EH²
En explicitant:	DE² = (CB – CF – GB)² + (GE – GH)²
Il faut évaluer les hauteurs des deux triangles rectangles:	DF = FG de CDB et GE de CEB
Et les longueurs au pied de ces hauteurs:	CF et GB

Calcul avec les angles en B
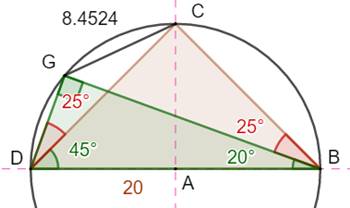
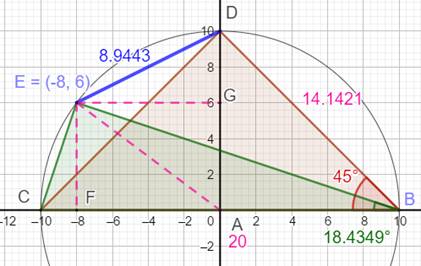
On connait la longueur de l'hypoténuse et les deux angles.		hypoténuse: CB = H = 20 alpha = 18,4349° bêta = 63,4349°
Calcul des hauteurs:
Calcul des pieds de hauteurs: (Aussi par méthode Pythagore, voir ci-dessous)
Reprise de la formule pour DE:		DE² = (CB – CF – GB)² + (GE – GH)² DE² = (20 – 2 – 4)² + (8 – 6)² DE² = (14)² + (2)² = 200 DE = 14,14213562 …
Formule littérale H = CB
Il n'y aucune relation entre alpha et gamma, donc pas de simplification possible. Tout au plus on peut simplifier les produits avec sin(a) · cos(a) = sin (2a) / 2.

Calcul avec les hauteurs
On connait la longueur de l'hypoténuse et celle des deux hauteurs DF et EG.	hypoténuse: H = 20 DF = 6 et EG = 8
Avec le triangle rectangle AEG:	AG² = AE² – EG² = 10² –- 8² = 36 = 6² GB = AB – AG = 10 – 6 = 4
Avec le triangle rectangle CDF:	AF² = AD² – DF² = 10² – 6² = 64 = 8² CF = 10 – 8 = 2
Longueur de la corde	DE² = (CB – CF – GB)² + (GE – GH)² DE² = (20 – 2 – 4)² + (8 – 6)² DE = 14,14213562 …

Calcul du triangle rectangle isocèle
Ca particulier où l'un des sommet est au milieu de l'arc en haut (D). L'un des triangles rectangles est aussi isocèle. Dans ce cas, l'un des angles vaut 45° et sin = cos = rac(2) / 2. Leur carré ou leur produit vaut 1/2.
Reprise de la formule pour DE:	) )
Avec sin(a) · cos(a) = sin (2a) / 2

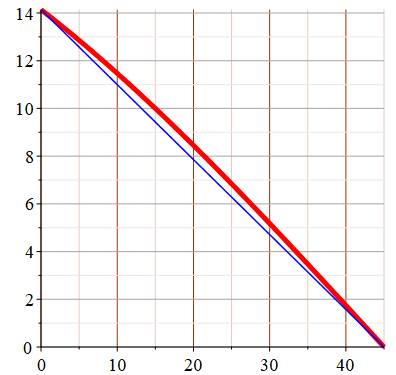
Graphe de la fonction Abscisse: angle en degrés de 0 à 45°. Ordonnée: longueur de la corde avec H = 20. Le droite montre que le graphe de la fonction (rouge) n'est pas une droite (bleue), mais pas loin. Exemples: alpha = 30° : DE = = 5,176… alpha = 20° : DE = 8,452… alpha = 10° : DE = 11,471…

Simplification de la relation
On peut transformer la racine d'un sinus double
En reprenant la formule de la longueur de la corde
Vérification

Retrouver la formule par construction
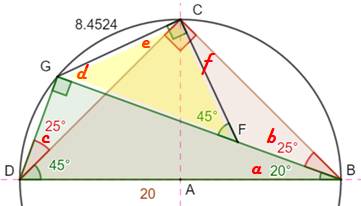
Simon Rivera propose une jolie démonstration géométrique de cette relation trigonométrique. Il utilise une construction intermédiaire astucieuse: Sur la figure, on a nos deux triangles rectangles inscrits dans un demi-cercle dont l'un est isocèle (DCB). On construit le point F sur BG tel que BF = DG. Le triangle CGF (jaune) est rectangle isocèle. Démontrons-le.
Le triangle DCB est rectangle isocèle: angle droit en C car inscrit dans le demi-cercle et CD = CB du fait de la symétrie.	c + 45° = 90 – a (triangle rectangle DGB) c = 45 – a or b = 45 – a, alors b = c
Les triangles DGC et BFC sont égaux (isométriques) car DG = BF, DC = BC, c = b	Alors, les angles e et f sont égaux. DCB étant un angle droit, GCF l'est aussi. Le triangle GCF est rectangle.
Dans le quadrilatère inscrit DGCB, la somme des angles opposés vaut 180°.	90° + d + a + b = 180° d = 180° – 90° – 45° = 45° Le triangle rectangle GCF est aussi isocèle.
Évaluons la longueur de la corde L = GC en fonction de DB = H et de l'angle a.
Or GF est l'hypoténuse du triangle rectangle isocèle GCF: GH² = L² + L²

Merci à Simon Rivera pour l'idée de cette démonstration (proposée le 30 août 2020)

Suite	Triangle rectangle Triangles – Formules Triangle – Résolution Rayon du cercle inscrit
Voir	Triangles héroniens Triangle – Introduction Triangle – Index Volume du tétraèdre Formule de Héron pour le trapèze
Sites
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/Corde.htm