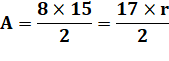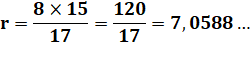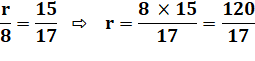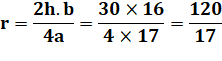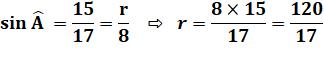|
||||||||||||||||||||||||||||||||||||||||
Voir Propriétés fondamentales
des triangles
![]()
|
Demi-cercle dans le triangle isocèle ou Cercle inscrit dans le losange Comment
calculer le rayon? Quatre méthodes sont proposées. |
|
|
||
|
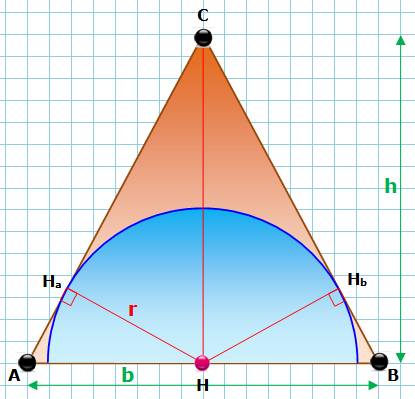
Problème Un triangle
isocèle dont la base mesure 16 et la hauteur 15. Un demi-cercle
inscrit comme indiqué sur la figure. Quel est
le rayon de ce demi-cercle? Remarques Le théorème
de Pythagore dans le triangle rectangle ACH indique:
= 8² + 15² = 64 + 225 = 289 Note: cette figure dupliquée vers le bas (symétrie
par rapport à AB) forme un losange avec son cercle inscrit. |
|
|
|
Calcul n°1 – Aire des triangles Aire du triangle
rectangle ACH. |
|
|
En isolant r On vérifie cette valeur sur la figure. |
|
|
Calcul n°2 – Triangles semblables Triangles rectangles ACH et AHHa |
Angle A commun Côté AH commun Angle en H et angle en C égaux car tous deux
compléments à 90° du même angle CAH. Les deux triangles sont semblables. |
|
Proportions dans les triangles
semblables |
|
|
Calcul n°3 – Cercle inscrit dans le
losange Le triangle isocèle symétrique par rapport à AB
est dessiné. Le quadrilatère ACBC' est un losange (quatre côtés égaux). On utilise la
formule du rayon du cercle inscrit dans le losange. |
|
|
Calcul n°4 – Trigonométrie On utilise l'évaluation double du sinus |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/DemiCerc.htm
|
![]()