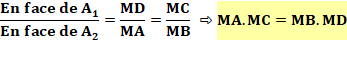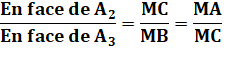|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Propriétés fondamentales
des triangles
![]()
|
ANGLES, TRIANGLES & CERCLES
|
|
|
||
|
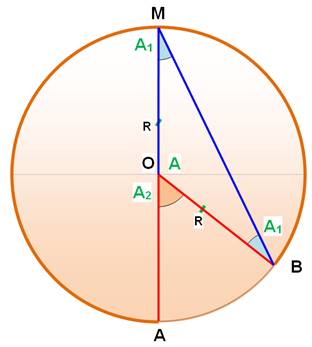
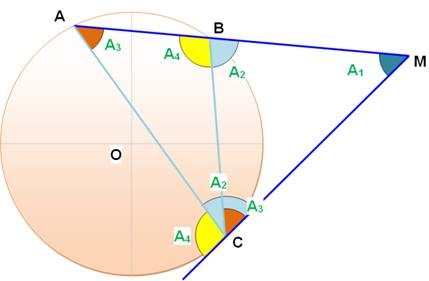
A + 2A1 = 180° = A + A2 A + 2A1 = A + A2 2A1 = A2 L'angle au centre AOB et l'angle
inscrit AMB, interceptant le même arc AB, sont l'un le double de
l'autre. |
|
|
|
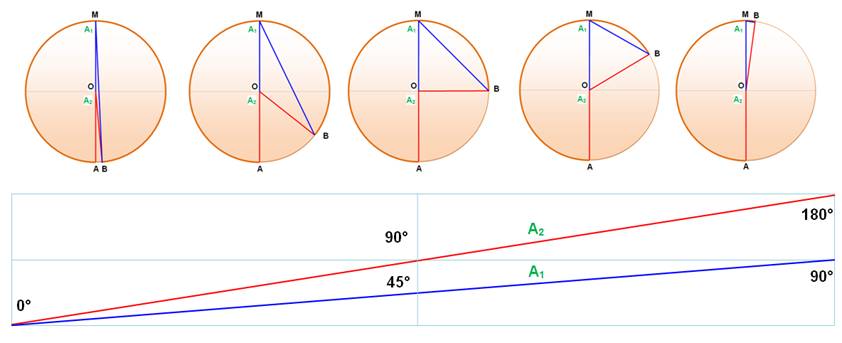
Variation relative des deux angles selon la position de B
|
||
|
|
||
|
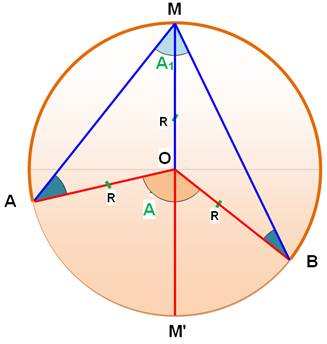
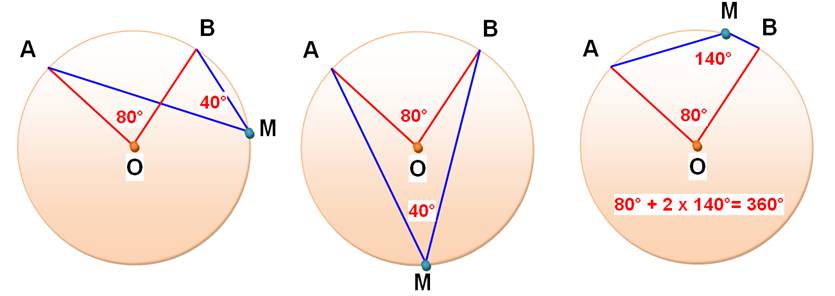
Théorème de l'angle au
centre
L'angle au centre AOB et l'angle
inscrit AMB, interceptant le même arc grand arc AB, sont l'un le
double de l'autre.
|
Somme des angles en bleu = angle en marron. |
|
|
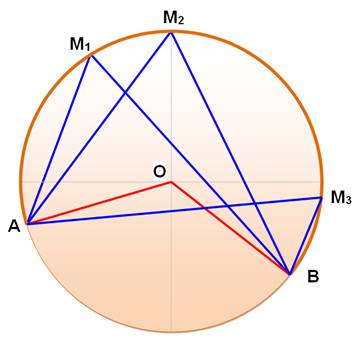
Théorème de l'angle inscrit
Tous les angles inscrits AMB, avec M situé sur le
grand arc AB, sont égaux et de valeur moitié de celle de l'angle au centre
AOB. Si M
est situé sur l'autre partie de l'arc AB, il est supplémentaire
aux précédents. Voir Quadrilatère inscrit dans un cercle |
|
|
|
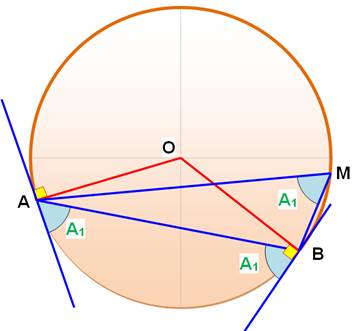
Les angles entre la corde Ab et les tangentes en
A et B sont égaux (A1). |
|
|
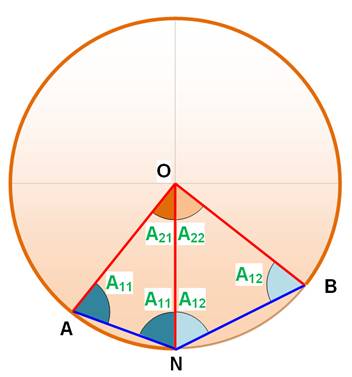
Cas du petit arc AB
A21 + 2 A11 = 180° A22 + 2 A12 = 180°
A2 + 2 A1 = 360° C'est d'ailleurs la somme des angles d'un quadrilatère.
A1 = 180° – A2 / 2 |
|
|
Exemples
|
|
|
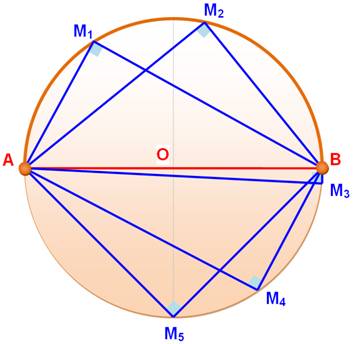
Cas ou AOB sont alignés
Un angle inscrit qui intercepte un diamètre est
un angle droit.
|
|
Suite Angles
dans le cercle
|
|
||
|
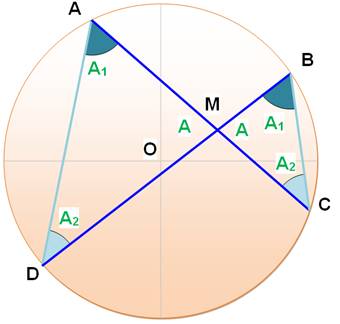
Les cordes se coupent en segments dont le produit
des uns et égal au produit des autres. |
Les triangles MAD et MBC sont semblables. MA.MC = MB.MD |
|
|
|
||
|
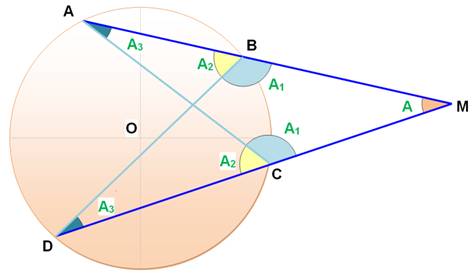
Les sécantes se coupent en segments tels que: MA.MB = MC.MD |
Les triangles MAC et MDB sont semblables. MA.MB = MC.MD |
|
|
|
||
|
|
Les triangles MAC et MCB sont semblables. MC² = MA.MB |
|
|
|
|
|
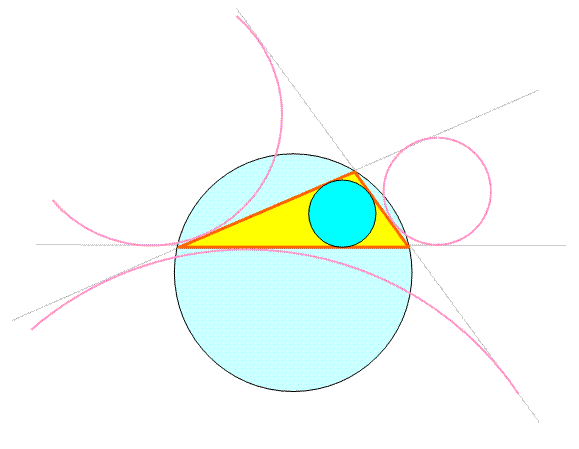
- 1 cercle inscrit petit
bleu foncé >>> - 1 cercle circonscrit grand
bleu clair >>> - 3 cercles exinscrits
rose >>> |
|
|
Leur centre est le point de concours des bissectrices intérieures
et extérieures (inscrit et exinscrits) et le point de concours des médiatrices
(circonscrit). Relation d'Euler dans le triangle R
est le rayon du cercle circonscrit r
est le rayon du cercle inscrit d
est la distance entre les centres de ces deux cercles Alors: d² = R² - 2R.r Note: Le cercle des neufs points est tangent aux
cercles inscrit et exinscrits. Propriété découverte par Feuerbach. |
|
Voir Carré et rectangle / Cercles et cercles
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/TrgCercl.htm |
![]()