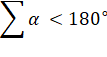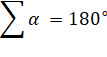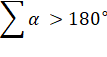|
|||||||||||||||||||||||||||||||||||||||
![]()
|
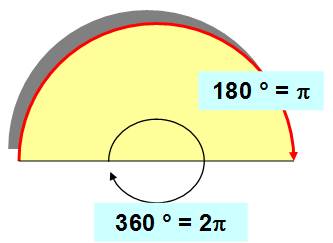
180°
dans le TRIANGLE
|
|
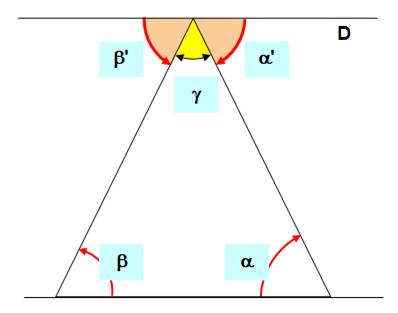
Pour tous les triangles, la somme
des trois
angles intérieurs est égale à 180° (un angle
plat ou deux
angles droits).
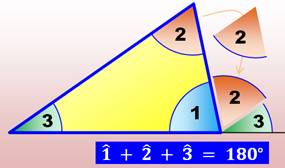
Un angle extérieur est égal à la
somme des deux autres intérieurs. Sur la figure: angle extérieur en 1 = 2 +
3. Si le triangle
est rectangle, les deux angles non-droits sont complémentaires (=90°).
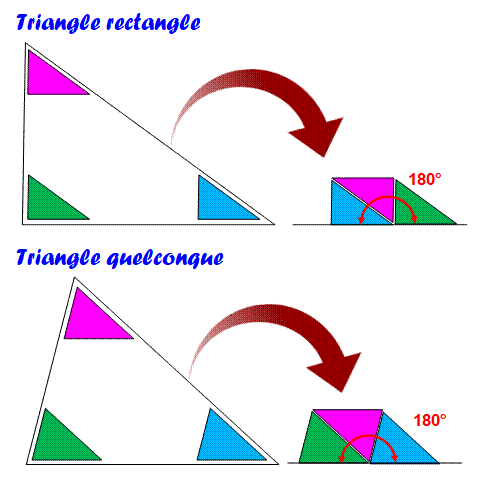
Cette propriété permet le pavage du
plan pour tout type de triangle >>> |
Voir Évaluation de CM1 / Autres relations avec les angles du
triangle
|
|
||||||||
|
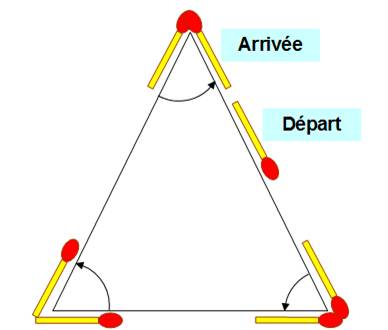
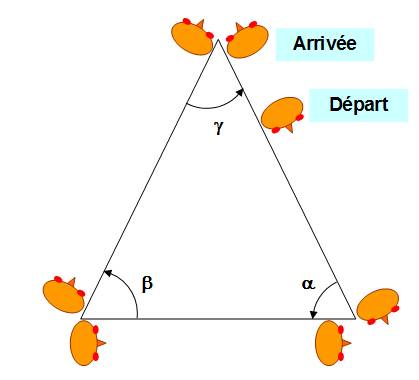
Le
demi-tour de l'allumette
. Voir Parcours du piéton
Géométries
non euclidiennes
Voir Nombre
180 / Triangle sphérique / Les trois géométries |
||||||||
|
|
|
|
La marche du piéton
(180 - 180 + 180 + 180 -
Un
piéton matheux
C'est une autre
version de la méthode allumette. |
|
|
|
|
|
Parallèle
|
|
|
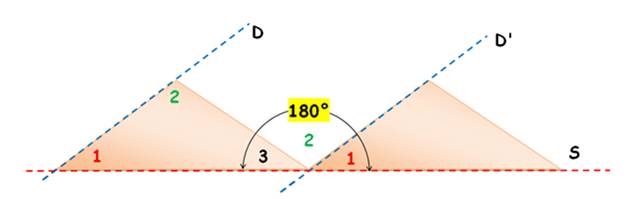
Alternative
Une démonstration
alternative est basée sur cette figure. |
|
Voir Angles alternes-internes / Parallèles et sécante
|
|
|||||||||||||||||||||
|
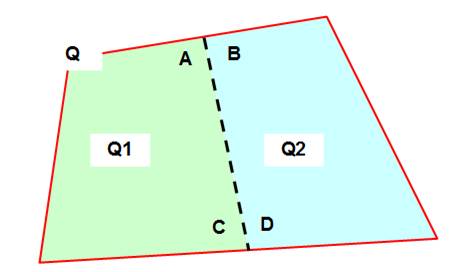
Coupé en deux
S1
pour Q1 et S2
pour Q2.
S
= S1 = S2
Propriété
Voir Nombre
360 En
pyramide
|
|||||||||||||||||||||
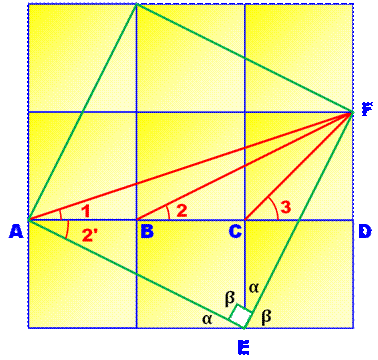
Cas amusant de deux fois trois carrés
|
Six
carrés identiques (2 x
3). Quelle
est la somme des angles 1 à 6?
Réponse: 180°
D'évidence, les angles
3 et 4, dans les carrés centraux, valent 45°. La figure est symétrique. On se
contente de monter que 1+2+3 = 90°. La
démonstration nécessite une petite construction supplémentaire. Le quadrilatère en
vert a ses quatre côtés égaux (diagonales de rectangles identiques); et
l'angle en E, par exemple, est droit (alpha + bêta = 90°). C'est un carré. AF est une diagonale
et l'angle FAE = 1 + 2' = 45°.
Les triangles rectangles ACE et FBD sont égaux (rectangles identiques, coupés en deux par
la diagonale); les angles sont égaux deux à deux: 2 =
2'. En rapprochant les
deux égalités: 1 + 2' = 1 + 2 = 45° Et sachant que 3 =
45°, nous avons: 1 + 2 + 3 = 90° Calcul
des angles
|
Voir Angles / Trigonométrie
|
|
|||||||||||
|
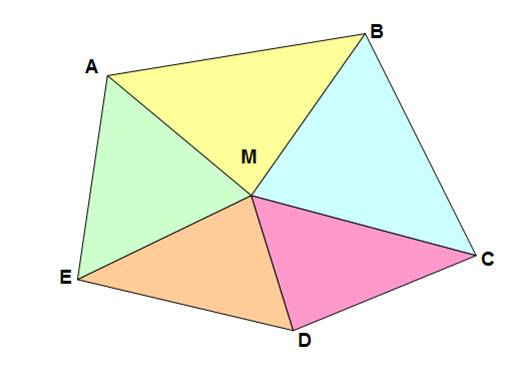
Généralisation
Exemple
Un côté de plus => Un triangle de plus
Propriété
Suite en Polygones - Propriétés |
|||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Propriété
Conséquence Il n'y a que cinq
polyèdres réguliers Polygone
à moins de 6 côtés
Cas limite où les
faces seraient pratiquement dans un même plan. La somme des angles
est donc strictement inférieure à 360°.
l'angle
atteint par le polyèdre qui posséderait trois de ces faces.
Que
cinq !
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/Trg180.htm |
![]()