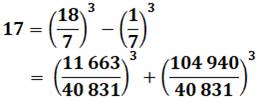nombre dix-sept en maths

Édition du: 04/11/2024

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10⁶ / 10⁹ / 10¹⁰⁰ / Infini
	-0-	10		20	30		40	50	60	70	80	90
	10	11		12	13		14	15	16	17	18	19

Nombre 17	Culture 17	Maths 17	Sciences 17
	Culture 17

Dix-sept

Seventeen

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 0001
Bases	101₄
Romain	XVII

Suite

Caractérisation du nombre

Chanceux d'Euler

Constructible

Cunningham (2⁴ + 1)

Déficient

Docile (amenable)

Emirp (17 et 71 premiers)

Fermat (n°3)

Fortuné

Impair

Leyland en x^y – y^x

Lucas premier (rang)

Narcissique de Keith

Perrin (10^e)

Premier

Premier bon

Premier de Chen

Premier de Genocchi

Premier de Pierpont (2⁴×3⁰ + 1)

Premier de Pythagore

Premier de Stern (n°1,non trivial)

Premier de Woodall

Premier de Fermat

Premier fort

Premier jumeau avec 19

Premier long

Premier permutable

Premier résistant

Premier supersingulier

Proth

Ramsey (3,3,3)

Woodall (2×3² – 1)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

C'est un œuf qui peut, en somme, faire dix-sept.

Jeu de mot avec "en somme" signifiant à la fois "en fait" et "en additionnant".

Voir Allographes / Pensées & humour

Chiffres et numération

17	N'est repdigit dans aucune base. Il n'est pas brésilien.
17 + 71 = 88	Devient repdigit lorsqu'ajouté à son retourné.
4 + 9 + 1 + 3 = 17 & 4 913 = 17³	Nombre digipuissant.
17 = 4 + 9 + 1 + 3 17³ = 4 913	Narcissique de Keith Égal à la somme des chiffres de son cube.

Addition et soustraction

p(17) = 297	Quantité de partitions du nombre.
17 = 8 + 9	Partition unique avec deux chiffres différents.
17 = 2 + 3 + 5 + 7 3 + 5 + 7 + 11 = 26 (pair) 5 + 7 + 11+ 13 = 36 (pair)	Somme de premiers consécutifs. Seul nombre premier somme de 4 nombres premiers consécutifs du fait de la présence du 2, pair. Sinon la somme de quatre impairs est paire.
17 = 1 + 4 + 9 + 3 = 1 + 6 + 8 + 2 = 2 + 5 + 7 + 3	Somme dans le triangle magique pannumérique.
17 = 2 + 2 + 13 = 3 + 3 + 11 = 3 + 7 + 7 = 5 + 5 + 7	Plus petit nombre quatre fois somme de trois nombres premiers.

Multiplication, division, diviseurs

17 = 1 x 17	Nombre premier. Voir 16 : couple 16 & 17
17 & 19	Quatrième paire de premiers jumeaux.
17 & 71	Nombres premiers circulaires ou permutables ou EMIRP.
17 > (13 + 19) / 2	Premier fort (2^e) supérieur à la moyenne arithmétique de ses voisins.
17 = 2 x 3² – 1	Nombre premier de Woodall d'ordre 3.
17, 19, 23, 29…247	Séquence de 16 nombres premiers en progression 2, 4, 6 …
n (n – 1) + 17	Cette formule donne de nombreux nombres premiers dont les 16 premières valeurs.
17, 6947, 13877, 20807, 27737, 34667, 41597, 48527, 55457	Suites de neuf nombres premiers en progression arithmétique de la forme a + kb avec: a = 17 et b = 6 930.
Avec 11 ou 41 …	Nombre chanceux d'Euler.
17 = 30 047 – 30 030	Nombre fortuné: différence entre primorielle et le premier juste plus grand (d'au moins 2).

n² + n + 17	Premier pour n = 0 à 15 d'autres... et
*abcdefghi abcdefghi*	est divisible par 17. Voir Nombres répétés
10 / 17 = 0,588235294…	Fraction qui représente une très bonne approximation du sinus de Pi/5. Base d'une construction approchée du pentagone régulier.
	Le plus petit nombre tel que son totient (phi) atteint 2 après quatre itérations.

Avec les puissances

17 = 1² + 4² = 2² + 2² + 3² = 1² + 2² + 2² + 2² + 2²	3 fois somme de n carrés, n 5
17 = 1³ + 2³ + 2³	1 fois somme de n cubes, n 5
17 = 1⁴ + 2⁴	1 fois somme de n puissances 4, n 5
17 = 2⁴ + 1 = 2^{2 à la puissance 2} + 1	Nombre de Fermat. Le 3^e, il est premier.
	Nombre multi-somme de type A² + kB². Record avec quatre représentations jusqu'à k = 10.
17 = 9² – 8² = 9 + 8	Différence de deux carrés de nombres consécutifs Comme tous les nombres impairs. Motif général.
	Différence entre puissances.
17 = 2³ + 3²	Nombre de Leyland.
17 = 3² + 2³ = 4² + 1³	Deux fois somme d'un cube et d'un carré. Le plus petit tel motif. Notez l'implication des quatre premiers nombres.
	Sommes de deux cubes rationnels. Trouvé par H. Dudeney.
17 = 1⁴ + 2⁴	Somme de puissances de nombres successifs.
17 = = partie entière de 17,255 307…	Comment faire 17 avec quatre 4.

En puissance

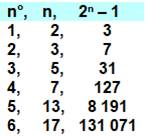
4,123 10…	Curiosité en 1234. Calcul de la racine.
	Deux nombres avec racines ayant des décimales proches à 0,0009… près.
2¹⁷ – 1 = 131 071	Nombre de Mersenne premier (n°6). Nombre parfait correspondant : 8 589 869 056 (le 6^e sur 8).
17² = 289 17² = 289 = > 1 2 et 7 8 9	Concaténation de deux premiers (2 et 89) Plus petit motif de cette sorte. Motif qui favorise la mémorisation de ce carré.
17² = 8² + 15² = 64 + 225 = 289	3^e triplet de Pythagore primitif.
17² = 2 x 12² + 1 289 = 2 x 144 + 1	Une des solutions de l'équation de Pell-Fermat: x² – 2y² = 1.
17² – 1 = 288 2⁵ • 3²	Deuxième nombre puissant en n² – 1. Liste: 3, 17, 26, 99, 485, 577, 1351, …
17² = 2 × 12² + 1	Motif carré en 2n² + 1.
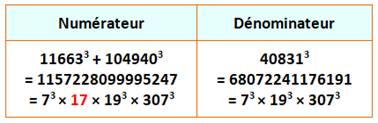
17³ = 47² + 52² = 17² + 68²	Cube somme de deux carrés.
17³ = 4 913 & 4 + 9 + 1 + 3 = 17	Nombre NESCHIP. Un des cinq tels motifs.
17³ = 4913	Nécessite 17 barres pour s'afficher sur la calculette.
…u¹⁷ = … u	La puissance 17^e d'un nombre quelconque se termine par le même chiffre des unités que le nombre lui-même.

	p = 17 est premier et la fraction est un nombre entier et premier. Seuls tels nombres avec p = (3, 5, 17 et 157).

Dénombrement, jeux et curiosités

	Jeu du quatre 4.
	C₈(n) est le nombre octogonal centré d'ordre n.
17 en symétrie	Il existe 17 groupes de symétrie plane ou de motifs de papier peint.
17 \| Groupe monstre	Premier supersingulier. Il divise le groupe monstre.

Autour du nombre

171819 = 19 091 x 9

Motif palindrome. Coquetterie avec le 19.

17/ 18 = 1 – 1/18

= 1/2 + 1/3 + 1/9

Base du jeu des divisions impossibles.

1/17 = 0,0588235294117647
0588 …

Fractions avec décimales dont la période est maximale (16) >>>

Notez que la racine numérique (preuve par 9) de la période est 9. Ce nombre est divisible par 9. Propriété valable pour tous les inverses des nombres premiers.

Ex: 1/ 23 = 0,0434782608695652173913 043…

Décimales

Puissance du nombre d'or.

Géométrie	17 groupes de symétries Ou 17 types de tapisseries. Number of wallpaper group.	>>>
	Il existe 17 façons distinctes d'arranger des polygones autour d'un point.
	17 points suffisent pour y trouver toujours un hexagone convexe. G. Szekeres et L. Peters	>>>
	17 itérations de la transformation du boulanger et on retrouve la figure initiale.	>>>
	Il est possible de découper une circonférence en 17 parts égales à la règle et au compas (heptadécagone)	>>>
	17 permutations de Dumont avec six nombres (Nombre de Genocchi).	>>>

Fractions avec 17
	Nombre premier long. La période du développement décimal de la fraction est maximale en une seule suite permutée pour toutes les fractions avec ce dénominateur.
Décimales 1/17 = 0,05882 35294 11764 70588 … 17 x 588 235 294 117 647 = 9 999 999 999 999 999 Toutes les fractions avec 17 au dénominateur possèdent 16 décimales répétitives par permutation circulaire. En rouge les 16 décimales répétitives; En bleu un groupe de 3 chiffres pour matérialiser la permutation circulaire.
Irrégularité de distribution Choisissez 17 nombres entre les intervalles créés par les 17 fractions (de 0/17 à 17/17). Facile! Mais la contrainte imaginée par Steinhaus est la suivante: Parmi ces 17 nombres, 16 doivent aussi se trouver dans les intervalles en 1/16; même chose pour les 1/15; etc. jusqu'à 1/2. Il a été prouvé que c'est faisable jusqu'à 17, mais que cela devient impossible à partir de 18.