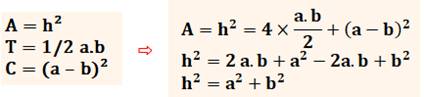NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 10 (180-199)		Page 11 (200-219)		Page 12 (220-239)		Page 13 (240-259)		Page 14 (260-279)
	Page 15 (280-299)		Page 16 (300-319)		Page 17 (320-339)		Page 18 (340-359)		Page 19 (360-379)

BRÈVES de MATHS – Page 17

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

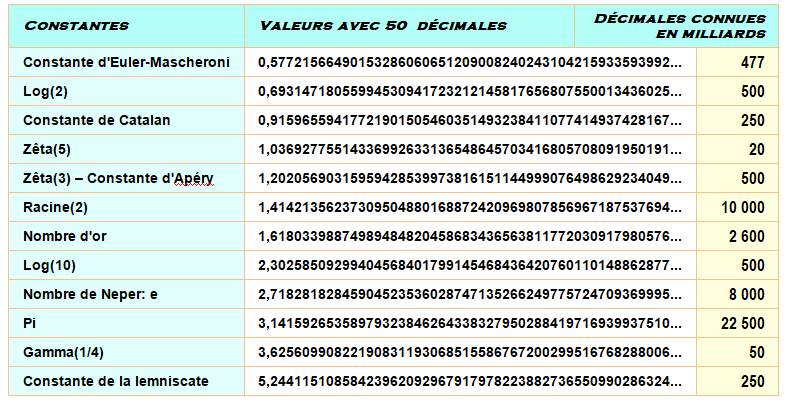
320. Constantes aux milliards de décimales
La course aux décimales est un exercice que les adeptes entreprennent non pas pour les décimales en elles-mêmes, mais pour le double défi : opérations sur de très grands nombres et algorithmique accélératrice de vitesse. Tableau des connaissances au 01/01/2019 La constante Pi est actuellement connue avec 22 500 milliards de décimales. Un "microfilm" de 1 cm de large avec une densité de 1000 chiffres par mm, il aurait une longueur de 2,25 km de long
Pour en savoir plus	>>> Liste des principales constantes et explications	Mise à jour sur le Site d'Alexander Yee

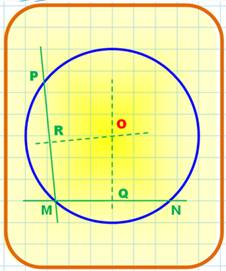
321. Centre du cercle
Centre du cercle Un point M quelconque sur le cercle; deux droites MN et MP, issues de ce point. Leurs médiatrices (RO et QO) se coupent en O. Le point O est le centre du cercle bleu.
Centre du cercle avec une règle La règle à bords parallèles coupe la circonférence en quatre points. Deux paires de droites reliant ces quatre points (verte et bleue). Elles se coupent en deux points et, la droite (rouge) qui les réunit passe par le centre du cercle. L'opération est renouvelée pour obtenir une seconde droite. L'intersection avec la première est le centre du cercle.
Brèves associées	>>> Cercles et angles >>> Rayon du cercle avec cordes		>>> Couronne
Pour en savoir plus	>>> Construction de la médiatrice et autres constructions usuelles >>> Constructibilité

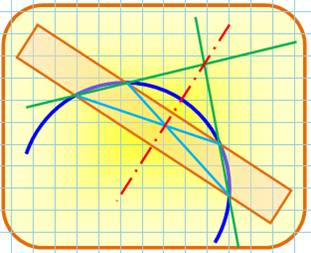
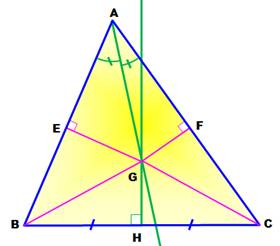
322. Tout triangle est isocèle (?)
Exemple de démonstration erronée et qui montre qu'il faut parfois travailler sur une figure la plus exacte possible. Construction Triangle quelconque ABC. Bissectrice en A. Médiatrice de BC. Point d'intersection G. Perpendiculaires aux côtés depuis G. Démonstration Bissectrice => GE = GF => trg AGE = trg AGF => AE = AF Médiatrice = >GB = GC => trg BGE = trg CGF => EB = FC En additionnant les deux égalités: AE + EF = AB = AF + FC = AC Les deux côtes AB et AC du triangle quelconque ABC sont égaux, le triangle est isocèle. Où se trouve l'erreur ?
Brèves associées	>>> Triangles et polygones – n x 180°		>>> Sangakus
Pour en savoir plus	>>> Tout triangle est isocèle – Solution		>>> Triangle isocèle

323. Magie avec des verres
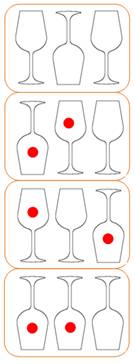
Le tour de magie commence par une présentation de la procédure: trois verres dont un retourné. chaque mouvement consiste à retourner deux verres à la fois (points rouges). en trois mouvements, les trois verres sont tous retournés (images ci-contre). On propose au spectateur de refaire la manipulation avec, à la clé, une récompense. On lui présente les verres comme indiqué à droite avec l'objectif de les mettre tous à l'envers. Le malheureux n'y parviendra jamais. Il perdra à tout coup. Ce tour a été proposé par Ian Stewart. Notez que dans la démonstration, il suffisait de retourner les deux verres extrêmes pour les mettre tous à l'envers. Avec la proposition de droite, le même mouvement remettrait tous les verres debout. Mais, on les veut tous à l'envers. Ce tour peut se faire avec des pièces de monnaies (proposé par Martin Gardner).				À gauche, on commence par 1 verre retourné pour arriver à 3 verres retournés. Chaque mouvement de deux verres conserve la parité. En haut, la parité de départ est 2 (deux verres renversés). Tout mouvement conservera cette parité.
Brèves associées	>>> Deviner quatre nombres consécutifs		>>> Âge répété
Pour en savoir plus	>>> Magie – Index		Plus sur le site: Cups and Downs

324. Le compte est bon
Comme au jeu télévisé, on donne un nombre à atteindre avec une suite de nombres donnés en utilisant seulement les quatre opérations (encadré jaune).
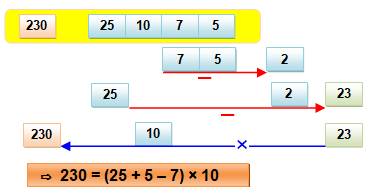
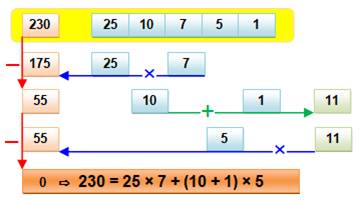
Faire 230 avec (25, 10, 7, 5, 1) On peut observer que 25 + 5 = 30 et 30 – 7 = 23 La multiplication pas 10 devient évidente.		Faire 230 avec (25, 10, 7, 5, 1) On peut tenter 25 x 7 = 175 et constate que le reste 55 est réalisable avec les chiffres restants.
Brèves associées	>>> Pourcentage – Un truc de calcul mental		>>> Multiplication rapide à pivot
Pour en savoir plus	>>> Faire 100 avec les chiffres >>> Jeux avec les nombres		>>> Les quatre opérations

Source de ces énigmes données pour juniors de 7 à 9 ans :

Défis de logique et de mathématiques – Antoine Houlou-Garcia – Larousse - 2017

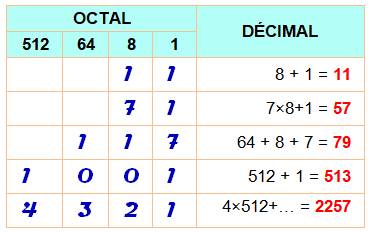
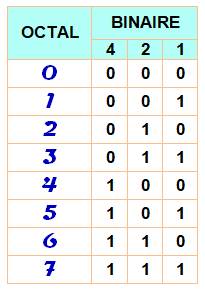
325. Octal
Octal L'octal est un système de numération à huit chiffres: 1, 2, 3, 4, 5, 6, 7. Après 7, on compte 10 qui est alors équivalent au 8 en décimal, puis 11 équivalent à 9, etc. Conversion Chaque position de chiffres correspond implicitement à une puissance de 8.		Additions en octal (exemples) Usage La conversion en binaire nécessite exactement trois bits. Une bonne façon de lire les nombres binaires en groupant les bits par trois et en lisant en octal. Exemple 111 000 101 001 se lit: 7051
Brèves associées	>>> Conversion binaire
Pour en savoir plus	>>> Octal		>>> Nombre 8

326. Théorème Pythagore – Chou Pei
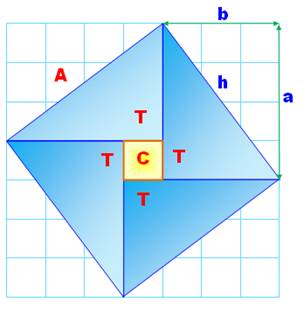
Le théorème de Pythagore Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés. Simple observation sur la figure de Chou Pei A = 4T + C (aire du carré bleu) T = ½ (4 x 3) = 6 (chaque triangle rectangle bleu) A = 4 x 6 + 1 = 25 = 5² L'aire du grand carré oblique bleu est 25. La longueur de son côté est 5. Chaque triangle rectangle a pour dimensions: (3, 4, 5). Ce qui vérifie le théorème de Pythagore: 3² + 4² = 5² Démonstration		Démonstration imaginée par Chou Pei Suan-Ching vers 1000 av. J.-C.
Brèves associées	>>> Théorème de Pythagore >>> Pythagore – Biographie		>>> Triangle 3 – 4 – 5 >>> Triplets de Pythagore
Pour en savoir plus	>>> Théorème de Pythagore >>> Triangle isiaque		>>> Carré en géométrie

327. Boson et champ de Higgs
À la recherche des forces unifiées aux premiers instants de l'Univers, les physiciens remontent le temps et comprennent l'unification des forces électromagnétiques. Leur modèle induit des médiateurs de forces (ici, le photon) de masse nulle. Pour inclure les forces nucléaires faibles, dont les bosons sont massiques, le modèle doit être aménagé. On imagine un temps lointain où ces bosons avaient une masse nulle et ils ont développé une masse plus tard. Pour l'expliquer, on invente un champ de type "mélasse" qui ralentit les bosons et leur confère l'illusion d'une masse. C'est le champ de Higgs et son boson médiateur associé (et son mystère quantique d'onde-corpuscule).		La masse des bosons passe en chaine aux quarks, aux neutrons et protons et, enfin à la matière toute entière. En 2012, avec un immense et puissant accélérateur, les savants ont mis en évidence une discrète anomalie qui témoigne du champ de Higgs. Oui, le boson de Higgs existe, mais il recèle encore bien des mystères ! Quelle est l'origine de tout cela et pourra-t-on un jour procéder à une unification plus profonde des forces ?
Brèves associées	>>> Relativité de Galilée et relativité d'Einstein
Pour en savoir plus	>>> Boson de Higgs		>>> Physique quantique

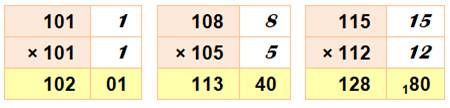
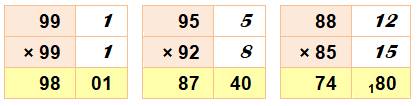
328. Multiplication proche de 100
Procédé 1) Notez les compléménts à 100 (colonne de droite). 2) Mettre leur produit à droite (dizaines et unités). 3) Précédé de 100 auquel on ajoute ou on retire la somme, selon que les nombres sont supérieurs ou inférieurs à 100. Justification (100 + a) (100 + b) = 10000 + 100 (a + b) + ab		101×101 = 10201 108×105 = 11340 115×112 = 12880 99×99 = 9801 95×92 = 8740 88×85 = 7480
Brèves associées	>>> Multiplication rapide		>>> Multiplications originales
Pour en savoir plus	>>> Multiplications mentales		>>> Produits algébriques

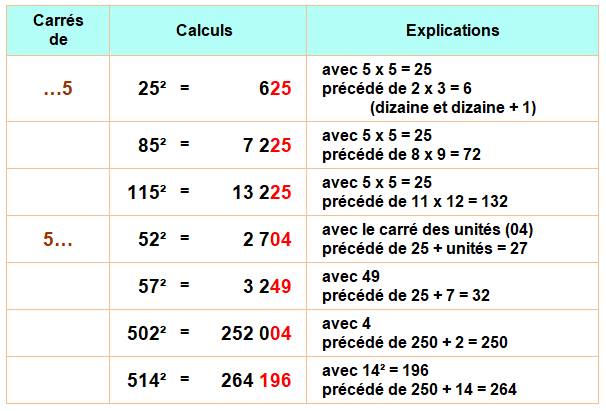
329. Carrés des nombres en 5
Bonnes astuces de calcul mental.
Brèves associées	>>> Multiplication rapide à pivot		>>> Multiplications originales
Pour en savoir plus	>>> Calcul mental des carrés		>>> Calcul mental – Index

330. Chemin eulérien de nombres

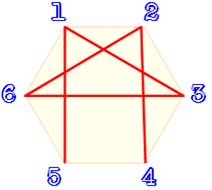
Suite de muliples et diviseurs

Vous connaissez le jeu qui consiste à suivre un dessin sans lever le crayon. On dit que le tracé suit un chemin eulérien.

L'idée ici consiste à exécuter un tracé reliant les nombres entiers avec pour règle que le nombre suivant est un multiple ou un diviseur du précédent.

Défi

Ainsi (Illustration), le nombre 1 divise 5, le nombre 3 est un multiple de 1, le nombre 6 est un multiple de 3, le nombre 2 est un diviseur de 6 et le nombre 4 est un multiple de 2

Le défi consiste à prolonger cette suite avec les nombres: 7, 8 … n.

Rapidement, il faudra se résoudre à créer deux chemins, puis trois …

Essayez !

Une des suites de multiples-diviseurs formant un chemin eulérien pour n = 6

5

1

3

6

2

4

Il existe trois autres telles suites pour n= 6, saurez-vous les trouver ?

Brèves associées

>>> Ponts de Königsberg

>>> Suite de Fibonacci

>>> La suite qui se lit

Pour en savoir plus

>>> Chemin eulérien de nombres

>>> Graphes eulériens

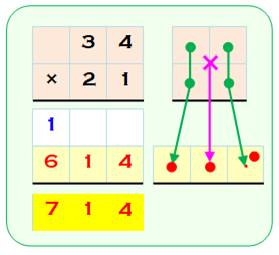
331. Multiplication mentale - TRUC
Principe Il existe un truc simple qui permet d'effectuer des multiplications rapidement, sans poser toute l'opération comme appris à l'école. L'avantage est de donner les chiffres de la gauche vers la droite les uns après les autres (avec un certain d'entrainement). Avec deux chiffres Prendre la colonne de gauche et multiplier (3x2 = 6). Prendre les deux colonnes et faire la somme des produits en croix (3x1 + 2x4 = 11) . Prendre la colonne de droite et multiplier (4x1 = 4). Les chiffres du résultat viennent les uns après les autres. Attention à tenir compte des retenues éventuelles.		Cas de 2 chiffres (détail et squelette du calcul)
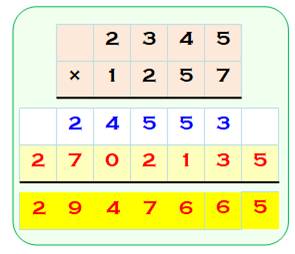
Avec plus de chiffres Le méthode avec plus de chiffres est une généralisation du cas à deux chiffres. Prenez successivement 1, 2, 3, 4, 3, 2, 1 colonnes, en allant de la gauche vers la droite. Faites tous les produits en croix en priorité, puis sur la dernière colonne verticale si elle existe. Sommez à chaque fois. Il est utile, sans habitude, de notez les résultats intermédiaires comme indiqué sur l'illustration, surtout pour tenir compte des retenues. Exemple avec le cas quatre colonnes 2x7 + 1x5 (produit en croix extrêmes); + 3x5 + 2x4 (produit en croix suivant); Pas de colonne verticale. Somme: 14 + 5 + 15 + 8 = 42 On pose 2 comme unité (jaune clair) et 4 comme retenue (bleu).		Cas de 4 chiffres (disposition pratique) 1x2 = 2; 1x3 + 2x2 = 7; 1x4 + 2x5 + 3x2 = 20; etc. Explications détaillées sur la page en lien
Brèves associées	>>> Multiplication rapide à pivot >>> Addition mentale		>>> Multiplications proches de 100 >>> Multilication économe
Pour en savoir plus	>>> Multiplications mentales avec nombre de chiffres quelconque – Le TRUC ! >>> Calcul mental – Index

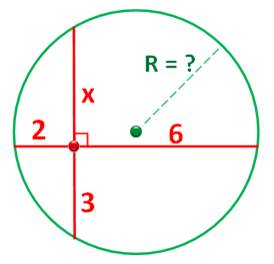
332. Rayon du cercle avec cordes
Énigme classique dans certains concours Avec ces trois mesures, retrouvez le rayon R du cercle. Deux théorèmes, à condition de les connaitre, donnent immédiatement la solution à ce défi. Théorème des cordes: 2 6 = 3 x = > x = 4 Relation donnant le rayon: 4R² = 2² + 3² + 6² + 4² = 65 R = 4,0311...
Brèves associées	>>> Centre du cercle - Construction		>>> Pizza – Choix de la taille
Pour en savoir plus	>>> Théorème des cordes sécantes		>>> Cercle – Index

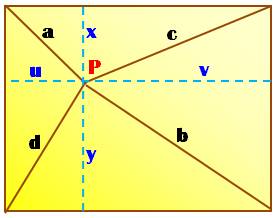
333. Point interne au rectangle
Le Point P interne au rectangle est quelconque. Propriété a² + b² = c² + d² Démonstration (simple) avec Pythagore a² + b² = u² + x² + v² + y² c² + d² = x² + v² + u² + y² Il y a bien égalité.
Brèves associées	>>> Un carré et deux triangles équilatéraux		>>> Pizza – Choix de la taille
Pour en savoir plus	>>> Rectangle		>>> Géométrie – Index

334. Nombres quadrillages
Exemple 12 = 2 (2 x 3) = 4 T2 = CC2 – 1 = 2² + 3² – 1 5² + 12² = 13² 10² + 11² + 12² = 13² + 14²		Propriétés Nombre quadrillage: 12 traits dans une grille 2x2. Quatre fois le deuxième nombre triangulaire. Nombre carré centré moins 1. Somme de deux carrés moins 1. Nombre central d'un triplet de Pythagore jumeau. Nombre central de cette somme de carrés. Ensemble, ces propriétés sont communes à toute une série de nombres: 4, 12, 24, 40, 60, 84, 112, 144, 180, 220, 264, 312, 364, 420, 480, 544, 612, 684, 760, 840, 924, 1012, …
Brèves associées	>>> Nombres géométriques		>>> Nombres de Harshad
Pour en savoir plus	>>> Nombres quadrillages

335. Équation de Bachet
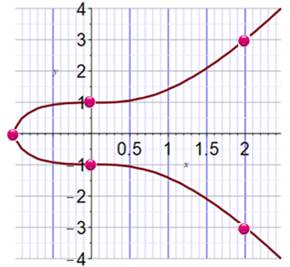
Bachet de Méziriac, en 1621, cherche des cubes et des carrés qui seraient proches à 2 près. Il trouve: 3^3 – 5^2 = 27 – 25 = 2 Fermat enchaine en défiant ses contemporains: montrer que la solution est unique en nombres entiers. Mordell démontrera en 1922 que les solutions pour x^3 – y^2 = k sont en nombre limité (y compris 0 solutions) Le cas de k = 1 (illustration) montre les cinq solutions possibles sur ces courbes dites elliptiques.		Graphe de y^2 = x^3 + 1 Solutions: (-1,0), (0,1), (0,-1), (2,3) et (2,-3).
Brèves associées	>>> Équations diophantiennes	>>> Équations et Racines – Un bon truc!
Pour en savoir plus	>>> Équation de Bachet	>>> Courbes elliptiques

336. Puissances et divisibilité par 5
Propriété La somme de cinq nombres consécutifs quelconques portés à la puissance p est toujours divisible par 5, sauf si p est un multiple de 4. Exemple littéral pour les carrés (n + 2)² + (n + 1)² + n² + (n – 1)² + (n – 2)² = 5 (n² + 2)		5^1 + 4^1 + 3^1 + 2^1 + 1^1 = 15 = 3 x 5 5^2 + 4^2 + 3^2 + 2^2 + 1^2 = 55 = 11 x 5 5^3 + 4^3 + 3^3 + 2^3 + 1^3 = 225 = 45 x 5 5^4 + 4^4 + 3^4 + 2^4 + 1^4 = 979 Non divisible 5^5 + 4^5 + 3^5 + 2^5 + 1^5 = 4 425 = 885 x 5
Brèves associées	>>> Divisibilité avec des factorielles		>>> Divisibilité par 11 – Méthode dominos
Pour en savoir plus	>>> Puissances et divisibilités par 5		>>> Divisibilité des formes polynomiales

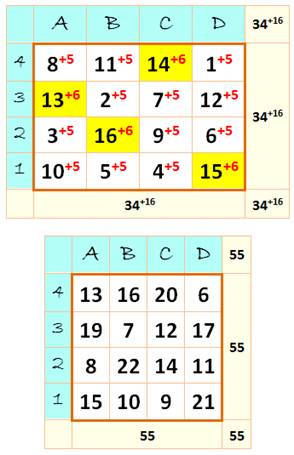
337. Carré magique à la demande
Tour de magie consistant à construire un carré magique 4x4 devant le public. La constante sera proposée par ce public. Disons que le choix s'est porté sur 55. La somme habituelle pour ce carré magique est 34. Prenons l'un de ces carrés de référence (nombres en noir dans le carré du haut). La différence entre ces deux nombres (21) est divisée par 4 (21 / 4 = 5 reste 1). Chaque nombre du carré magique jusqu'à 12 sera augmenté de 5 et les suivants seront augmentés de 6 (addition en rouge) Notez qu'alors chaque ligne, chaque colonne et chaque diagonale est bien augmentée de 21. En bas le carré magique demandé, additions effectuées. Pour ajouter de l'éclat à ce tour, vous partirez d'un carré vierge et vous demanderez au public de vous indiquez la prochaine case à remplir.
Brèves associées	>>> Preuve par 9 et sa magie	>>> Deviner quatre nombres consécutifs
Pour en savoir plus	>>> Ce tour de magie expliqué	>>> Magie – Index

338. Code César – Brève Junior

Code de Jules CÉSAR

Jules César est un empereur Romain qui a vécu vers les années 50 avant Jésus-Christ. Il y a plus de 2000 ans. Il faisait souvent la guerre et il envoyait des messages secrets à ses armées.

Par exemple, peux-tu décoder celui-ci?

Le Message de MAMIE et PAPY

Voici un nouveau message avec un nouveau code secret comme l'aurait fait Jules César.

Je te conseille de regarder la solution, car il est très dur sans connaître le truc.

Cette fois, il faudra dessiner une grille de carrés.

SOLUTION

Pour chaque lettre, il suffit de prendre la lettre qui vient après dans l'alphabet: le A devient B, le B devient C, et ça continue.

La première lettre est un K. et devient L, car le L est la lettre qui vient après le K dans l'alphabet. Puis le N devient O, et ainsi de suite …

Voici la solution complète:

Message secret

K

N

T

H

R

D

.

D

S

.

B

K

D

L

D

M

S

Message décodé

L

O

U

I

S

E

.

E

T

.

C

L

É

M

E

N

T

SOLUTION

Pour trouver le message, il faut dessiner une grille de quatre carrés par quatre carrés.

Tu écris les lettres secrètes sur la première case, mais en descendant

Regarde où se trouvent les quatre premières lettres BEAC, sur la colonne jaune de gauche.

Brèves associées

>>> Cryptologie – Approche

>>> Orthographe des nombres

Pour en savoir plus

>>> Code César

>>> Cryptologie

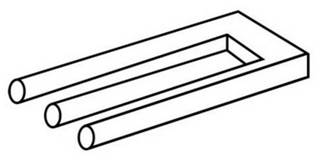
339. Fourchette à trois dents
Illusion de la fourchette de Bivet		Illusion des étagères
Brèves associées	>>> Preuve par 9 et sa magie		>>> Deviner quatre nombres consécutifs
Pour en savoir plus	>>> Illusions d'optique		>>> Magie – Index

Retour	Brèves de maths – Page 16
Suite	Brèves de maths – Page 18
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve17.htm