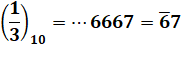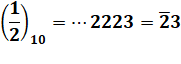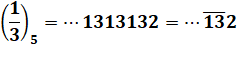Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 02/10/2022 M'écrire Brèves de Maths

INDEX Types de nombres Décomposition des Nbs Inventaire des nombres Nombres par leur nom	Nombres p-adiques
	Introduction	Nombres décadiques	Séries
	Opérations	Nombres triadiques	p-adiques – Théorie
	Division et inverse	P-adiques périodiques	p-adiques – Pratique
	Automorphes		Tables de p-adiques

Faites un double-clic pour un retour en haut de page

NOMBRES p-adiques Division et inverse Nombres p-adiques et divisions. Comment les calculer.
	Sommaire de cette page >>> Approche >>> Inversion par multiplication à trous >>> Divisions simples >>> Fractions	Débutants Nombres Glossaire Nombres

Approche			haut
Nombres ordinaires	1/3 = 0,333…	En effectuant la multiplication: 3 × 0,333… = 0,999… = 1
Nombre p-adiques	1/3 = …66666710 1/3 = …13131325 1/3 = …01010112

Inversion par multiplication à trous		haut
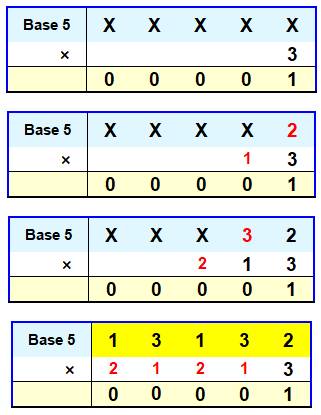
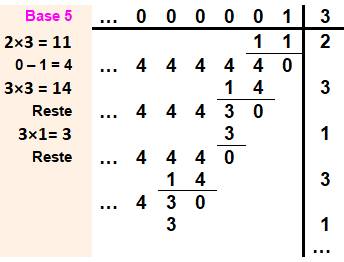
En base 5-adique, inverse de 3 On pose une multiplication par 3 dont le multiplicande est inconnu (XXXXX). Le résultat étant 1, on cherche les valeurs de X par essais de multiplications successives. Première étape: quel nombre, multiplié par 3 donne 1 en base 5. Impossible. Il faut une retenue. Quel nombre multiplié par 3 donne 11 en base 5. C'est 2 . En effet: 2 × 3 = 610 = 115. Etc.

Divisions simples		haut
Disons-le tout de suite, la division des nombres décadiques n'est pas toujours possible.	La division est toujours possible pour les p-adiques vrais, c'est-à-dire lorsque p est premier.
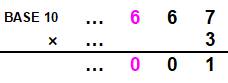
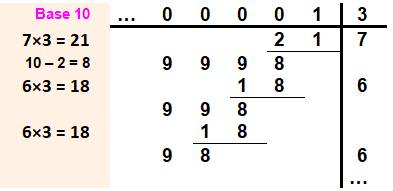
En base 10-adique Pour une fraction comme (1/3)10 , on peut la calculer en décadique selon le même principe que pour une division classique. Valeur et notation de la période
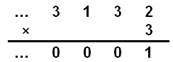
En base 5-adique Pour vérification, on peut poser la multiplication: …222223 × 2 = 10000001
On vérifie que le produit donne 1: En effet: 3 x 2 = 6, 11 en base 5; je pose 1 et je conserve 1 en retenue. Puis, 3 x 3 + 1 = 10, 20 en base 5. Et 3 x 1 + 2 = 5 soit 10 en base 5. Finalement 3 x 3 + 1 = 10 soit 20 en base 5.

Fractions	haut
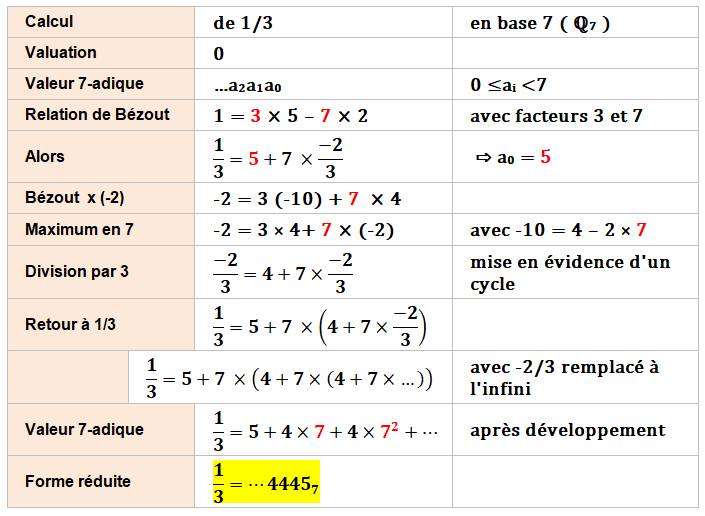
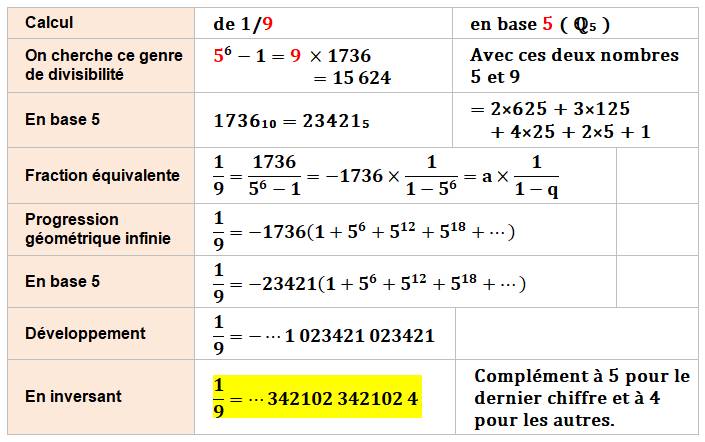
Exemple de calcul d'une fraction en base 7 Voir Valuation / Théorème de Bachet-Bézout Calcul avec multiplication et division Calcul avec mise en évidence d'une progression géométrique infinie Voir Progression géométrique

Haut de page

Retour	Nombres entiers et les autres Nombres décadiques Nombres p-adiques – Théorie
Suite	Nombres p-adiques périodiques Nombres p-adiques en pratique
Voir	Fractions - Glossaire Fractions continues Introduction aux nombres premiers Inventaire des nombres Nombres premiers et nombres composés Représentation des nombres Suites
Sites	Voir références en première page
Cette page	http://villemin.gerard.free.fr/NombrCar/Padique4.htm