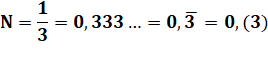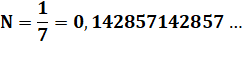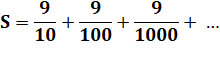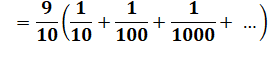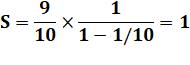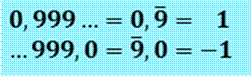|
Édition du: 02/10/2022 |
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES p-adiques Périodiques ou INVERCIMAL Nombres
périodiques en inversion miroir des nombres périodiques classiques. Une bonne
appréciation de l'intérêt des nombres p-adiques en termes opératoires (pour faire
des opérations). |
||
|
|
Sommaire de cette page >>> Notation des nombres périodiques >>> Cas de …999,0 >>> Addition >>> Multiplication >>> Opposé et soustraction >>> Inverse et division |
Débutants Glossaire |
|
Un nombre
périodique est composé de décimales dont certaines se répètent à
l'infini. La partie
répétitive, nommée période, est surlignée ou, parfois, mise entre
parenthèses. |
|
|
|
Un nombre périodique
p-adique est son symétrique miroir. Notez que
l'on peut commencer la période à différentes places. |
|
|
|
Le nombre
ordinaire 0,999… vaut 1. En effet: |
S = 0,999… 10S = 9,999… 9S
= 9 + S
S = 1 |
|
|
Autre
méthode de calcul via les séries
géométriques de raison 1/10. |
|
|
|
Identité d'Euler sur les séries, utilisée pour
calculer le retourné p-adique. À retenir
|
Or …999 = - 0,999… P + S = 0 (Euler) P + 1 = 0 P = …999,0 = -1 |
|
|
Sur le
même modèle: |
…9990,0 = – 10 …99900,0 = – 100 …99912,0 = – 100 + 12 = – 88 |
|
|
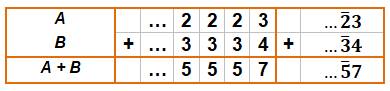
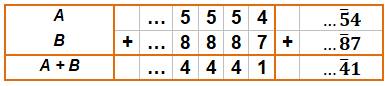
Addition
simple, sans retenue |
|
|
|
Avec
retenue à droite |
|
|
|
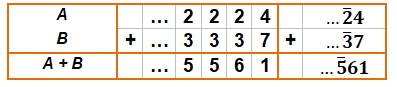
Avec
retenue à gauche, la retenue se propage à gauche; elle est projetée à
l'infini. |
Notez que dans la notation de droite les trois
poinrs sont inutiles. |
|
|
Avec
périodes différentes |
|
|
|
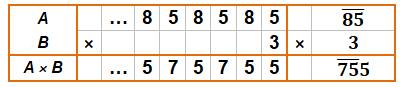
p-adique
par un nombre |
|
|
|
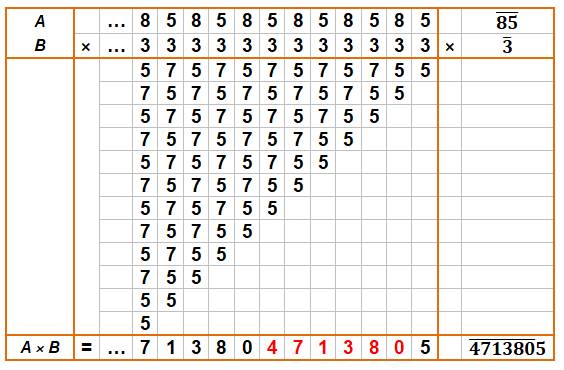
p-adiques
entre eux. Il est nécessaire
de pousser les calculs suffisamment pour mettre en évidence la
période. |
|
|
|
Soit le
nombre A, trouver son opposé B tel que A + B = 0. Il s'agit de remplir la ligne B pour disposer du
résultat nul. |
On remarque que l'opposé est un nombre sans signe
négatif. On ne conserve les chiffes que sur la période
(rouge). Chaque chiffre est le complément à 9, sauf le
dernier (à droite) qui est complément à 10. |
|
|
Avec une
partie fixe à droite. |
|
|
|
Soustraction |
Elle consiste à ajouter l'opposé. |
|
|
Soit à
calculer l'inverse B de A, tel que A × B = 1. Il s'agit de remplir la ligne A pour disposer du
résultat unité. |
Pour savoir quel chiffre placer à droite, on se
reporte au tableau ci-dessous. Pour le premier chiffre: 7x = 1, l'unité de la
multiplication (ou le nombre mod 7) est égale à 1. Au dessus du 1 dans le
tableau, on trouve 3 (logique 3 × 7 = 21).
|
|
|
Division |
Elle consiste à multiplier par l'inverse. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |