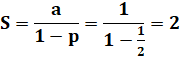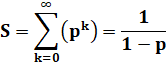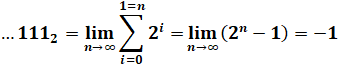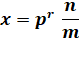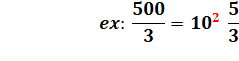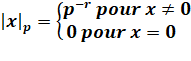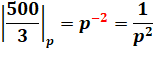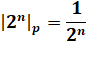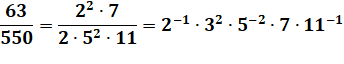|
Édition du: 02/10/2022 |
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES p-adiques Séries Les nombres p-adiques ont été introduits par Kurt Hensel à la fin du XIXe siècle, dans le but de
transposer à la théorie des nombres les méthodes des développements
en séries entières utilisées dans la théorie des fonctions d'une
variable complexe. Dit-autrement, l'histoire des nombres
p-adiques débute par le développement en série (somme infinie) des
nombres. Il s'agit d'un développement en série d'une nature particulière
puisque la somme ne semble pas converger.
L'exemple ci-dessous montre le développement de la fraction 1/3 en
base 5 et sa notation p-adique, laquelle est: soit dans l'ordre des
coefficients; soit dans l'ordre inverse (notation courante, en jaune).
|
||
|
|
Sommaire de cette page >>> Séries convergentes et conversion p-adique >>> Identité d'Euler sur les séries >>> Levée du mystère de la convergence: nouvelle
norme |
Débutants Glossaire |
Une relation mystérieuse, voire absurde !
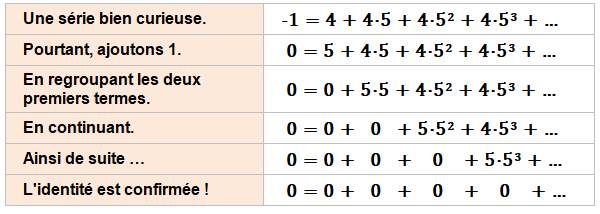
Hensel a rendu ce type de convergence logique
dans le monde des p-adiques.
Voir Somme
de Ramanujan
|
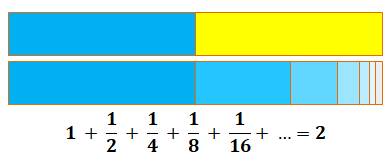
Progression géométrique On connait la série indiquée à droite qui
converge vers 2 et on sait calculer la limite de cette progression
géométrique de raison 1/2 et de premier terme a = 1:
|
Exemple
|
|||
|
Formule générale pour a = 1 Formule valable que si p < 1. |
|
|||
|
Convergence et nouvelle topologie Et si, on prenait la série avec les nombres et
non leur inverse ? La raison devient 2 et le calcul donne -1 ! Oui,
on s'affranchit de la condition d'un raison comprise entre 0 et 1. Résultats aussi étranges avec d'autres valeurs. |
|
|||
|
Conversion d'un nombre p-adique en
nombre ordinaire |
On a à faire à une progression
géométrique de raison p² dont la somme est 1 / (1 – p²) si p < 1. Avec les nombre p-adiques, par définition, on
ignore cette condition. |
|||
|
Série géométrique à convergence
inattendue OUPS ! La convergence de cette somme n'est
assurée que pour p de -1 à +1. En p-adique,
on fera l'hypothèse qu'elle converge toujours et que la limite est donnée par
la même formule. |
|
|||
|
Identité d'Euler
sur les séries Prenons cette série doublement infinie. Pour l'évaluer, on lui associe la série
multipliée par x. On retrouve évidemment la même suite. Si x est différent de 1, la série converge vers
0. Voir Somme
qui rend fou par Euler / Brève
895 |
|
|||
|
Partage et nouvelles identités Du fait que la somme est nulle, tout partage de
la série en deux parties sera telle que la première partie sera égale à
l'opposée de l'autre. |
|
|||
|
Exemples La notation avec
surlignement montre les chiffres qui sont répétés. Il est parfois souhaitable
de conserver quelques chiffres pour mieux exprimer la répétition. |
|
|||
|
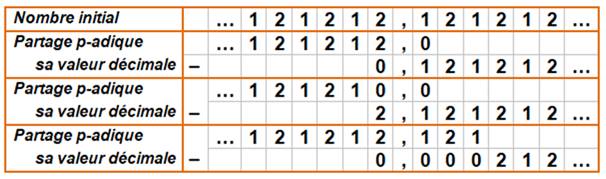
Avec partage Trois exemples dont le premier est avec un
partage à la virgule. Valable pour base 3 ou plus. |
Lecture de ces nombres avec la notation en surligement Cas
1: le nombre ordinaire Cas
2: le nombre ordinaire Cas
3: le nombre ordinaire |
|||
|
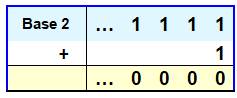
Exemple avec le nombre 1 en base 2 Comme: 1 = 0,999 … en décimal. On a: 1 =
0,111… en binaire. En ajoutant 1 à ce nombre, on obtient …000 en
2-adique (ou dyadique). On a donc:
…1112 = – 1 et son
développement en série tel qu'indiqué. En retirant 1, on trouve cette limite étrange: la
série en 2n converge vers 0. Pour donner un sens à la formule, il faut définir
une nouvelle métrique. |
|
|
|
Tout nombre rationnel x (différent de 0) peut
s'écrire comme indiqué avec r et n des
entiers relatifs et m un entier positif. |
|
|
|
La norme d'un nombre
p-adique est définie par: Cette norme satisfait l'inégalité forte du
triangle (elle est non archimédienne et spéciale aux nombres p-adiques):
|
|
|
|
Conséquence: les grandes puissances de 2
"sont devenues petites". |
|
|
|
Soit un nombre et sa factorisation. Pour tout premier pk , impliqué dans
cette factorisation, la norme est égale à p-k. |
|
|
|
La norme de la différence constitue une métrique
sur les nombres p-adiques |
Surprenant:
pour p = 5, le nombre 135 est plus proche de 10 que de 35. 135 = 10205 10 = 205 35 = 1205 135 – 10 = 10005 norme 10-3 135 – 35 = 4005 norme 10-2 |
|
Voir P-adiques- Théorie
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |