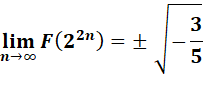|
Édition du: 02/10/2022 |
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES p-adiques Approche avec les nombres
automorphes Les
nombre p-adiques sont des nombres classiques mais retournés dans un miroir.
Ils se prolongent éventuellement vers la gauche au lieu de la droite pour les
nombre classiques. Il existe
des nombres classiques qui se comportent aussi de cette manière. Voyons cela
comme présentation du concept de p-adique. |
||
|
|
Sommaire de cette page >>>
Approche >>>
Carrés automorphes et décadiques >>>
Équation >>>
Amusement "p-adique" >>>
Nombres de Fibonacci |
Débutants Glossaire |
|
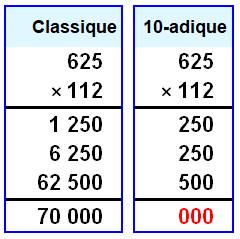
Nombres particuliers Il existe des nombres qui produisent une grande
quantité de zéros lorsqu'ils sont multipliés. C'est le cas de 625 et 112 dont le produit est 70
000. On peut même ajouter des chiffres à droite pour obtenir de plus en plus
de zéros. Nombres décadiques En 10-adique, la multiplication est tronquée à gauche
au-delà de la quantité de chiffres des opérandes. Ainsi en 10-adique: 625 × 112 = 000, un
produit nul. Diviseurs de zéro De tels nombres, non nuls, créant un produit nul
sont appelés des diviseurs de zéros. Évidemment, avec les nombres ordinaires, il n'y a pas de diviseurs de zéro. |
Exemple
Suite avec de plus en plus de zéros 5 625 ×
2 112 = 11 880 000 15 625
× 22 112 = 345 500 000 515 625 × 122 112 = 6 2964 000 000 |
|||
|
Carrés automorphes Nous connaissons des nombres qui, élevés au
carré, se terminent par ces nombres eux-mêmes: les nombres
automorphes (dits de Gergonne et Lucas). En ajoutant des chiffres à gauche, on obtient des
nombres avec de plus en plus de chiffres identiques à droite. Une race de nombres particuliers caractérisés par
de plus en plus de chiffres à gauche. Idée de nombres
p-adiques. |
Nombres et leurs carrés avec même
terminaison
Propriété valable pour les cubes et toute
puissance supérieure. |
|||
|
Nombres p-adiques Ils sont comme les nombres ordinaires, mais avec
cette particularité à gauche:
|
Calculs Les opérations sont exécutées
comme pour les nombres ordinaires, avec les mêmes retenues. Dans le cas des nombres entiers, le résultat est
tronqué pour avoir la même taille que le plus grand des opérandes. |
|||
|
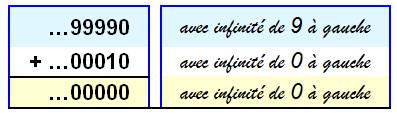
Opposé d'un nombre p-adique Cette addition a une somme nulle. Ce qui veut
dire que 10 est l'opposé (cad. un inverse pour l'addition) du nombre
décadique. Soit: …99990 = – 10 |
Exemple
|
|||
Voir Exemple naturel de
nombre décadique
|
Produit automorphique Voyons le carré de ce nombre automorphe: Ce
nombre se retrouve intégralement en fin du carré. Soit le produit 10-adique indiqué en tronquant le
produit à la quantité de chiffres des opérandes. Notez que le même nombre au cube produira le même
phénomène et cela d'ailleurs pour une puissance quelconque. En notant x ce nombre, on a: |
1787109376² = 3193759921787109376 17871093763 = 5707598300918769841787109376
17871093763 = 5707598300918769841787109376
|
|
|
Produit nul Voyons maintenant cette multiplication. Le produit de x et de (x – 1) donne le 10-adique
nul. Nul également avec le carré de x ou une puissance
quelconque. Que nous inspirent ces résultats ? Voyons cela au paragraphe suivant. |
1787109376 × 1787109375 = 193759920000000000
1787109376² × 1787109375 = 5707598297725009920000000000
|
|
|
Théorème fondamental de l'algèbre La quantité de racines complexes d'un polynôme
est égale à son degré. |
Ce n'est pas le cas en
décadiques (ℚ10). |
|
|
Exemple x² – x = 0 Deux solutions évidentes 0 et 1. C'est tout ! |
En p-adiques, il y en a deux
autres (u, v). |
|
|
Les deux autres racines (u et v) présentent les
relations habituelles des racines d'une équation du second degré. |
Pour x² – x + 0 = 0: u + v = 1 (coefficient de x) u · v = 0 (constante) |
|
|
Si x² = x, ces deux nombres partagent au moins
les mêmes unités |
5² = 25 & 6² + 36 Ce sont les deux seuls nombres à
un chiffre ayant cette propriété d'automorphisme. |
|
|
Il est tout à fait possible de poursuivre les
recherches avec les dizaines, puis les centaines, etc. |
25² = 625 et 76² = 5 776 |
|
|
Après plusieurs itérations Hors les unités, les chiffres de même rang se
complémentent à 9. La somme vaut 1 et le produit vaut 0. |
u = … 12 890 625 v = … 87 109 376 …12 890 625 + … 87 109 376 = …0001 …12 890 625 × … 87 109 376 = …0000 |
|
|
De tels nombres qui se prolongent sans fin à
gauche sont des nombres décadiques automorphes. Ces deux nombres sont des diviseurs de zéro. Cette particularité disparait pour les p-adiques
avec p premier. |
Le fait que le produit de ces
deux nombres est nul montre que (ℚ10) n'est pas intégre: hors 0
et 1, il existe des nombres dont le produit est nul.
|
|
Bilan
|
Nous venons de faire la connaissance de nombres
qui se prolongent indéfiniment vers la gauche. Tout ce qui a été dit en base 10 pourrait l'être
dans une base quelconque. Avec les nombres ordinaires, ce sont les chiffres
à droite qui perdent de l'importance. Plus les chiffres de gauche (poids
forts) sont proches et plus les nombres se ressemblent (la différence est
faible). Avec les p-adiques, c'est l'inverse: plus les
chiffres de droite sont proches et plus les nombres se ressemblent. Reste à définir ce type de proximité. |
![]()
|
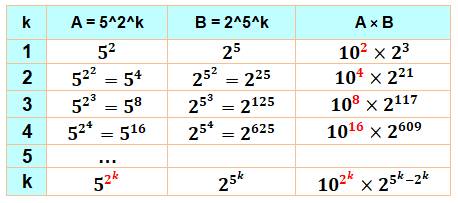
Propriété Les
nombres 2 et 5 à la puissance en 5k et 2k sont singuliers
en ce sens qu'ils conservent leurs chiffres avec k croissant. De plus leur
produit est composé de plus en plus de zéros.
Motif singulier avec ces nombres
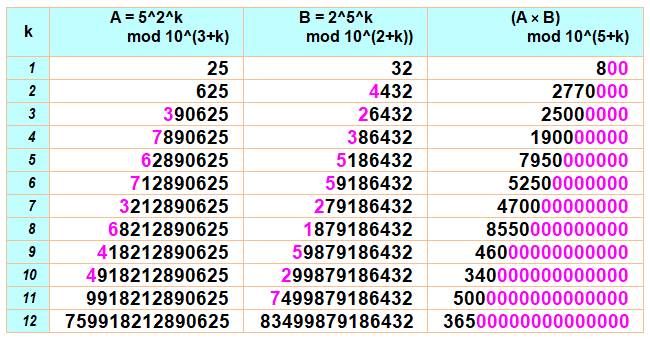
tronqués à gauche Les
nombre A et B sont calculés pour les valeurs de k de 1 à 12. On ne
conserve qu'un certain nombre de chiffres à droite: k + 3 pour A et k + 2
pour B. Le
produit de ces nombres tronqués est calculé tout en ne conservant que k + 5
chiffres à droite. Les
valeurs additionnelles à k sont ajustées pour montrer l'apparition des
nouveaux chiffres tout en conservant un chiffre de tête.
Note: mod 103
, par exemple, veut dire: ne conserver que les trois derniers chiffres. Voir Nombre
376 – Autres valeurs / Pépites de nombres Forme p-adique En éliminant ce nombre de tête on obtient une
forme p-adique, c'est-à-dire qui se prolonge à l'infini vers la gauche. Exemple: …90625 × …6432 = …0000 Explication de la production des
zéros Il n'est pas étonnant de trouver de nombreux
zéros dans le produit de nombres en 2 et 5 avec 2 x 5 = 10. En fait, les nombres non tronqués en produisent
beaucoup plus que ceux figurant sur le tableau ci-dessus. Ce tableau montre les calculs en puissance de 10.
L'exposant en rouge, indique la quantité de zéros qui se retrouvent dans le
produit des nombres complets (non tronqués). Cette quantité est égale à
l'exposant du nombre 5. Le nombre en puissance de 2 (B) étant de loin plus
grand que celui en puissance de 5 (A).
|
|
Voir Puissance de
2 / Puissances
de 2 à 5 / Nombres
automorphes
|
La suite de
Fibonacci recèle également une certaine structure p-adique; en fait
2-adique (dyadique). Dans la liste des nombres de Fibonacci, on sélectionne
ceux de rang en puissance
de 2 et on les convertit en binaire. Exemples On prend alors un nombre sur deux pour former la
liste du haut et les autres pour la liste du bas. Pour chacune des listes, les chiffres terminaux
sont de plus en plus communs et converge vers un nombre 2-adique qui se
trouve être:
|
4, 11 16, 11011 64, 10111011 256, 10000111011 1024, 1101000111011 4096, 01001000111011 16384, 0111001000111011 65536, 111111001000111011 8, 10101 32, 0000101 128, 011000101 512, 00111000101 2048, 1110111000101 8192, 100110111000101 32768, 110000110111000101 |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |