|
Édition du: 07/04/2025 |
|
INDEX |
Échecs – Cavalier |
||
|
|
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
Cavalier – Mouvements Problème
classique: inverser la position des blancs et des noirs en un minimum de
mouvements. |
||
|
|
Sommaire de cette page >>> Rappel du mouvement du cavalier >>> Liberté de mouvement >>> Inverser les blancs et les noirs >>> Mouvements du cavalier sur tout l'échiquier |
Débutants Glossaire |
Anglais: The move of a
chess knight, knight's tour
|
En
1512, Guarini invente ce petit problème de déplacement des cavaliers sur
mini-échiquier 3x3. Comment inverser les blancs et les noirs en un minimum de
coups? Attention, pas si simple! Anglais: Guarini's knight-switching problem. |
|
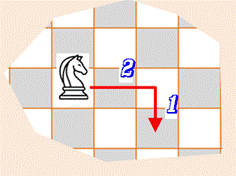
Cavalier Le cavalier (ou cheval) est une des pièces du jeu
d'échec, représenté par une tête de cheval. Il y en a deux blancs et deux noirs sur un
échiquier. Mouvement en L du cavalier Deux pas dans une direction (horizontale ou verticale) Autre vision: le cavalier
avance d'une case puisse saute en oblique sur une case voisine. |
Exemple de mouvement du cavalier
Notez qu'à
chaque mouvement du cavalier, la couleur de la case change. |
|
Les 24 (= 4!) trajets possibles
du cavalier pour rejoindre la position six cases plus bas
C'est la représentation de l'hypercube
Voir Brève 58-1156
|
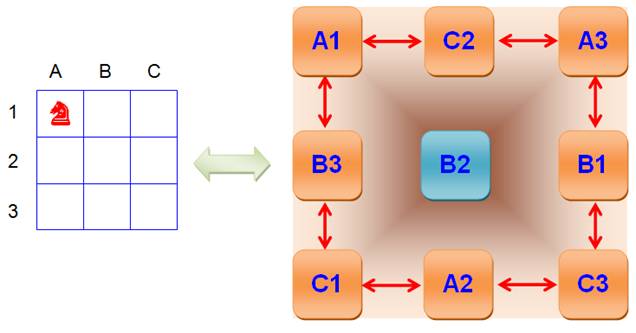
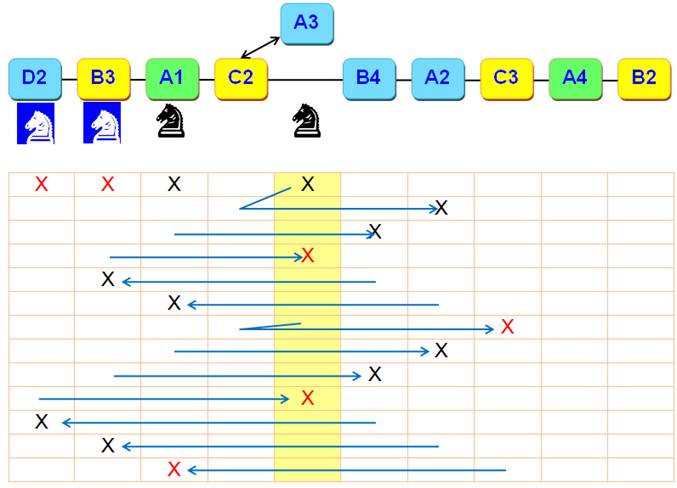
Échiquier 3 x 3 Parcours possible du cavalier sur un plateau de 3
x 3. Le graphe
traduit que depuis la position A1, le cavalier ne peu aller qu'en positions
C2 ou B3. Etc. Le graphe montre que, hors la case centrale,
le cavalier maîtrise toujours deux positions et qu'il peut parcourir toutes
les cases de la couronne. Ce schéma équivalent établi sous forme d'un
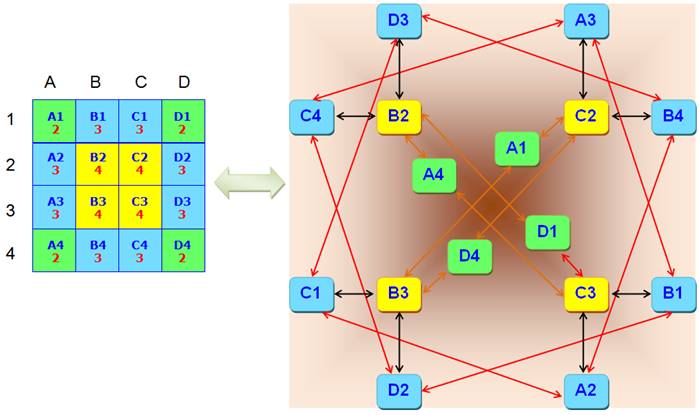
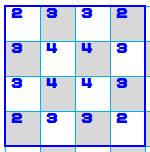
graphe permet de résoudre plus facilement certains problèmes. Échiquier 4 x 4
Le nombre en rouge dans le tableau indique la
quantité de déplacements du cavalier depuis cette case. Avec ce graphe, on peut imaginer les mouvements
du cavalier dans le cas où on supprime des cases:
Avec ce genre de graphe, on peut facilement imaginer des casse-tête.
On peut notamment montrer que le périple
du cavalier est impossible (passer partout, une seule fois). |
|
|
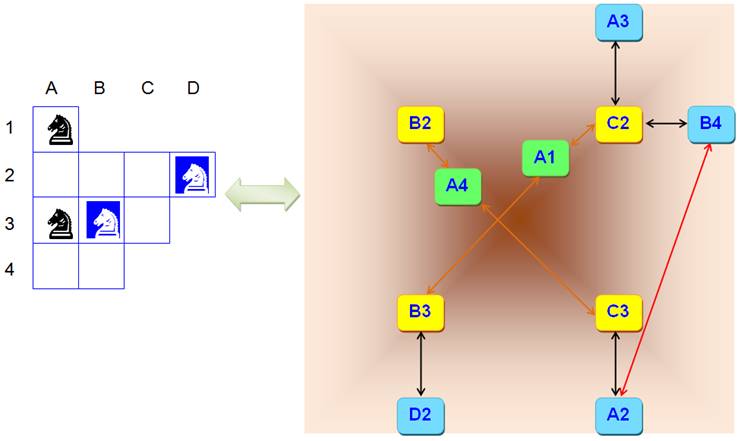
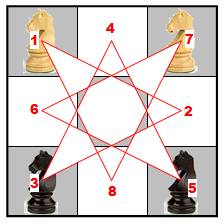
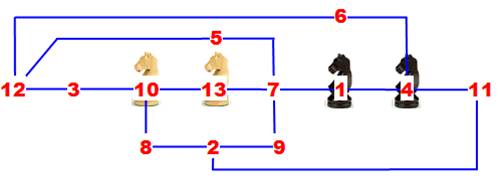
Voici un casse-tête classique, difficile à résoudre sans l'aide du
schéma équivalent. Avec cette partie de l'échiquier seulement, inverser les cavaliers
bleus et les cavaliers verts.
Mise à plat du graphe et résolution
|
|
Voir Jeux et énigmes
|
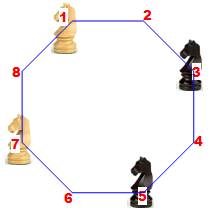
Résolution avec le
graphe équivalent, puis le graphe simplifié
Le graphe représente les
possibilités de mouvements de chacun des cavaliers. La solution est évidente
à partir du graphe simplifié. Il suffit de faire tourner d'un cran l'ensemble
des cavaliers de quatre pas. Une rotation d'un cran nécessite quatre
mouvements (Ex: 1-2, 3-4, 5-6 et 7-8). La solution minimale exige seize
mouvements. |
|
Bonus:
même problème, inverser les noirs et les blancs en un minimum de mouvements.
Graphe
équivalent
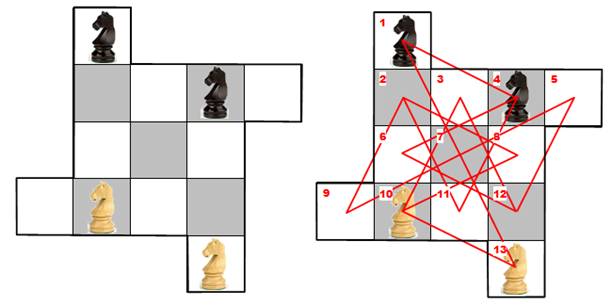
Solution:
mettre les deux blancs en voie de garage en 5 et 9: 5 mouvements. Amener les Blancs en
position finale: 6 mouvements. Amener les noirs en
position finale: 5 mouvements Total: 16 mouvements.
Les cases (2, 3, 6, 8, 11 et 12) ne sont pas utilisées. (b) 13 -- 7 -- 1
(cavalier blanc rangé sans être passé par le garage) (c) 5 -- 7 -- 13
(cavalier noir garé maintenant rangé) (d) 4 -- 6 -- 12
(l'autre cavalier noir débute sa route) (e) 10 -- 8 -- 2
(l'autre cavalier blanc aussi) (f) 12 -- 3 -- 10
(l'autre noir la finit) (g) 2 -- 11 -- 4 (et
l'autre blanc aussi). On gagne ainsi deux
mouvements parce que dans cette solution, le cavalier blanc ne passe pas
forcément par une voie de garage. |
Merci à Denis Vekemans pour cette solution
plus optimisée et sans doute minimale
|
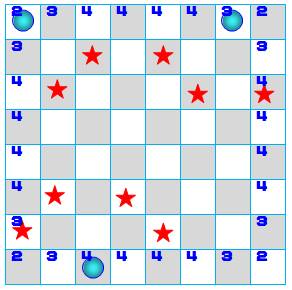
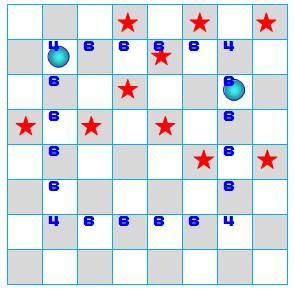
Tous les mouvements On cherche toutes les possibilités de déplacements
du cavalier à partir d'une des cases de l'échiquier classique 8×8. Mouvements à partir des bords La bille bleue symbolise une position du cavalier,
et ses possibilités de mouvements sont matérialisées en rouge. À partir de ces trois modèles, on reporte la
quantité de mouvements dans toutes les cases correspondantes de la bordure. On dénombre: Mouvements à partir de la couronne
suivante Même principe avec bille bleue et triangles
rouges comme modèles. On dénombre: Mouvements à partir du centre Sur toutes les cases centrales, le cavalier à
toute liberté de se déplacer, soit 8 mouvements. Il y 4×4 cases, soit 16 × 8 = 128 possibilités Tous les mouvements Total: Formule pour un échiquier n × n Première couronne: (4 × 2) + (8 × 3) + (4(n-4) × 4) Deuxième couronne: (4 × 4) + (4(n-4) × 6) Centre: (n-4)² × 8 Total: 8n² – 24n + 16 = 8 (n –
1)(n – 2) = 16 Tn Mouvements du cavalier selon la
taille de l'échiquier Cette suite est égale à 16 fois la suite des nombres
triangulaires. C'est aussi la suite des nombres 16-gonaux
centrés moins 1. |
Échiquier 8 × 8:
336 mouvements possibles
Échiquier 4 × 4:
48 mouvements possibles
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()