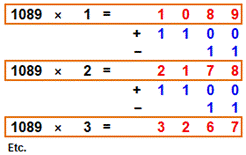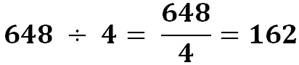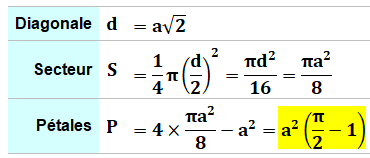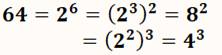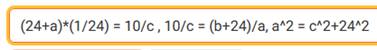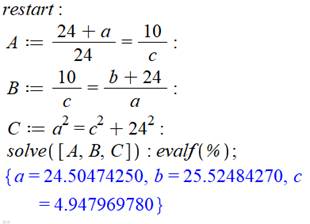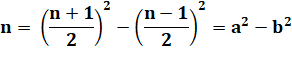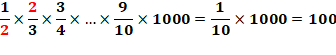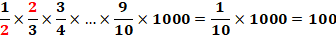NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/09/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 50 (980-999)		Page 51 (1000-1019)		Page 52 (1020-1039)		Page 53 (1040-1059)		Page 54 (1060-1079)
	Page 55 (1080-1099)		Page 56 (1100-1119)		Page 57 (1120-1139)		Page 58 (1140-1159)		Page 59 (1160-1179)

BRÈVES de MATHS – Page 58

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

1140. Nombre 1089 = 1100 – 11
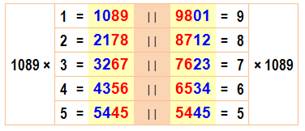
Observations Observez la table de multiplication du nombre 1089. Voyez les unités, les dizaines, les centaines et les milliers. Saut de 1 à chaque fois, en plus ou en moins. Observez également la symétrie de la table (nombres retournés).		Table de multiplication par 1089
Explication Le nombre 1089 est égal à 1100 – 11. De sorte que pour passer d'un multiple au suivant il suffit: d'ajouter 1 aux centaines et aux milliers, et de retirer 1 aux unités et aux dizaines. Principe valable pour de nombreux nombres en 111… – …11 comme 109.		Passage d'un multiple au suivant
Brèves associées	>>> Nombre 1023		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Multiplications type 1100 – 11 >>> Nombre 1089		>>> Palindrome >>> Multiplications >>> Nombres retournés

1141. Équation avec racines
Défi Cette équation est publiée sur Internet. Sa résolution semble compliquée. Elle est pourtant simple: une question de manipulation des exposants des puissances. Piste Rappel: la racine d'un produit est égale au produit des racines. Élevons les deux membres au carré. Alors le carré d'une racine carrée est le nombre lui-même. Avec deux élévations au carré, tous les radicaux de racine carrée disparaissent Alors x est la racine cubique de 3 à la puissance 4. La seconde solution utilise les exposants sous forme de fractions sachant que la racine énième de x est notée x^1/n.		Deux solutions
Brèves associées	>>> Équation avec racines cubiques		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Calculs avec les puissances		>>> Puissances fractionnaires

1142. Achats-Ventes
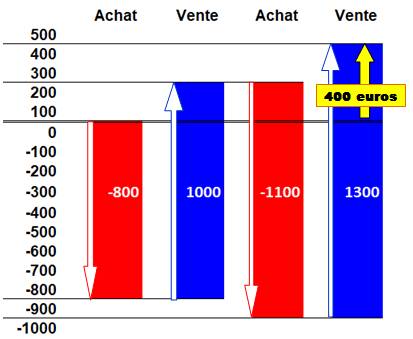
Énigme J'ai acheté une vache: 800 euros. Je l'ai vendue: 1 000 euros. Je l'ai rachetée: 1 100 euros. Je l'ai revendue: 1 300 euros. Quel est mon gain ? Solution On peut facilement arriver à effectuer un raisonnement erroné. Le moyen le plus sûr pour aboutir au résultat juste consiste à visualiser les dépenses et recettes successives et d'observer les soldes. Dit-autrement: visualiser le porte-monnaie.		Suite aux dépenses et recettes successives, le solde s'établit à 400 euros
Brèves associées	>>> Énigme des 30 euros >>> Le faux billet de 50 euros		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Énigmes d'achats-ventes		>>> Amusements logiques

1143. Division à traits
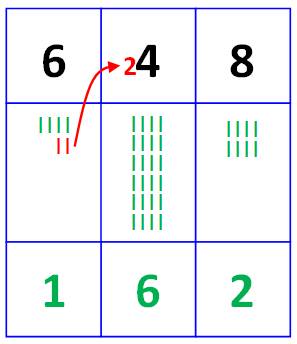
Division originale et facile Une sorte de retour au boulier: les nombres sont représentés par des traits. Pour réaliser la division par 4, on les arrange par paquets de 4 (ici en vert). Opération réalisée pour chaque chiffre du nombre en partant de la gauche. On note la quantité de paquets pour chaque chiffre. S'il reste des traits (ici en rouge), on reporte leur quantité comme dizaines pour le chiffre suivant. Bilan		Division à traits
Brèves associées	>>> Division euclidienne (classique)		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Multiplication à traits >>> Nombre 4		>>> Division – Bases >>> Boulier – Abaque

1144. Aire des pétales
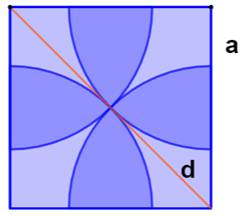
Aires de quatre pétales formées par les quarts de cercles centrés sur les sommets du carré et dont le rayon est égal à la moitié de la diagonale.			Pétales = 4Secteurs – Carré
Brèves associées	>>> Aire du rectangle dans le triangle	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Poster: aires avec les cercles	>>> Défis en géométrie – Index

1145. Puissances multiples
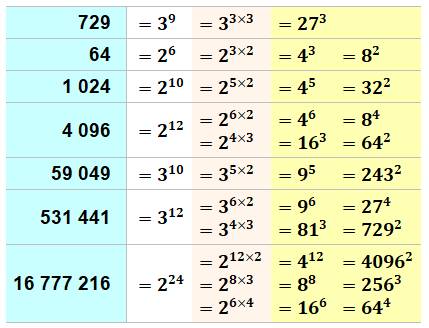
Propriété Une puissance dont l'exposant k est un nombre composé peut se mettre sous la forme de nombres à la puissance ayant pour exposant un diviseur de k. Exemple (Voir tableau) Le nombre 64 est la puissance 6 de 2. Or, le nombre k = 6 est un nombre composé égal à 2 × 3. Alors, 64 est une puissance à la fois de 2 et de 3. Écriture avancée		Exemples
Brèves associées	>>> Puissances – Un truc de calcul		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Nombres puissants		>>> Diviseurs >>> Nombre 16 777 216

1146. Citerne remplie au quart
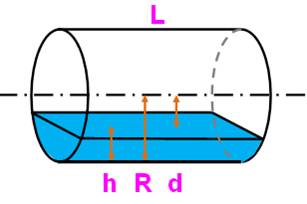
Problème direct Une citerne cylindrique est en position horizontale. Elle contient du gazole. La jauge indique h = 1/4 du diamètre du cylindre. Quelle est la quantité de gazole ? Le calcul du volume connaissant la hauteur est donné par une formule qu'il suffit de calculer: Problème inverse Nous devons remplir la cuve au quart de sa capacité en surveillant la hauteur. Mais qu'elle est la hauteur à atteindre. Dans l'équation, on connait A et R, il faut calculer h. Or, l'inconnue h est enfouie dans un arccos et sous une racine. Pas simple !!! Plus que cela, c'est impossible. La seule manière de s'en sortir consiste à effectuer des approximations successives		Citerne Solution Pour remplir la citerne au quart, la hauteur à atteindre est: h = 0,596… Anglais: Quarter-Tank Problem
Brèves associées	>>> Verre ballon penché		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Problème de la citerne (explications)		>>> Équations transcendantes

1147. Somme des puissances de 9
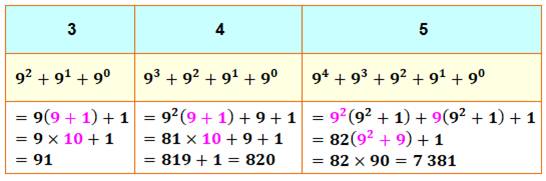
Calcul simple des sommes des puissances successives de 9 (par factorisation) Erratum en bas à droite, lire: 82x90 +1= 7 381 Liste des premières sommes des puissances de 9 1, 10, 91, 820, 7381, 66430, 597871, 5380840, 48427561, 435848050, 3922632451, … Notez l'alternance 0, 1 pour les unités. Ce sont les nombres de la forme (9^n – 1)/8 qui sont aussi les nombres triangulaires différences de carrés; aussi les repunits (1, 11, 111, …) en base 9
Brèves associées	>>> Calcul avec des puissances	>>> Brèves Calculs – Index
Pour en savoir plus	>>> Somme des puissances de 9	>>> Calculs de sommes

1148. Racine de racines
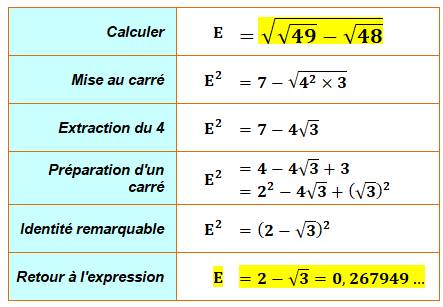
Calculer la racine de racine de 49 moins racine de 48. La première idée consiste à se débarrasser du radical principal en élevant l'expression au carré. Ensuite, on essaie justement de trouver un carré, du moins la forme développée du carré d'une somme.
Brèves associées	>>> Racine triple de 2		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Calculs avec des racines		>>> Racines carrées

1149. Voirie minimale
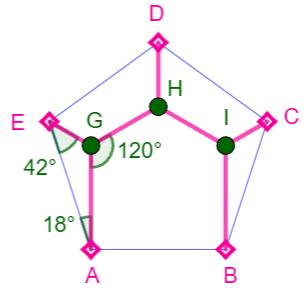
Voirie minimale pour cinq villes Cinq villes au sommet d'un pentagone régulier. Toutes les villes doivent être reliées entre elles. Cependant, l'urbanisme cherche à minimiser le coût. Quelle est la disposition des routes qui minimise la longueur totale du réseau routier ? Arbre de Steiner Le réseau le plus court est obtenu en ajoutant trois points intermédiaires (point de Steiner). Il se troue que ces points sont entourés de trois angles à 120°. Construction (en suivant la figure): dessiner un pentagone régulier; trois verticales à partir de A, B et D; l'angle de 42° à partir de E; intersection en G; l'angle de 120° en G; intersection en H; horizontale en G; intersection en I. dessiner l'arbre de Steiner (segments roses)		Arbre de Steiner d'ordre 5 La longueur du réseau est 3,891… c, avec c le côté du pentagone.
Brèves associées	>>> Graphe – Devinettes		>>> Brèves Graphe – Index
Pour en savoir plus	>>> Arbres de Steiner		>>> Pentagone

1150. Nombres en racines
Observation Il est toujours possible d'exprimer un nombre entier sous la forme d'une racine carrée. Et cela, de diverses manières. C'est à Ramanujan que l'on doit les formules qui expriment un nombre entier sous la forme de la racine d'un produit incrémenté de 1. Le produit est celui de deux nombres distants de deux unités. Explication Le produit sous la racine est l'identité remarquable: (a – 1) (a + 1) = a² – 1. Ajoutez 1 et vous obtenez un carré.		Formules
Brèves associées	>>> Carré et cubes – Belle égalité		>>> Brèves Relations – Index
Pour en savoir plus	>>> Racines carrées >>> Identités remarquables		>>> Ramanujan

1151. Géométrie complexe !
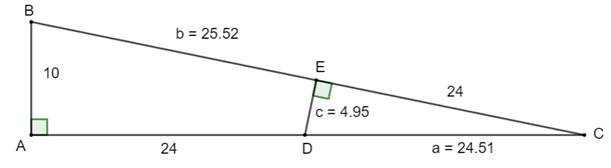
Problème Sur cette figure formée de deux triangles rectangles, les valeurs de a, b et c sont inconnues. Comment les calculer ? Pistes Les triangles rectangles ABC et EDC sont semblables et, nous pouvons établir des proportions. Avec les triangles rectangles, nous pouvons appliquer le théorème de Pythagore. Assez d'équations pour résoudre un système à trois inconnues. Oui, mais la résolution est très complexe et à solutions réelles et complexes … Aujourd'hui, les logiciels mathématiques sont d'un grand secours ! Ci-dessous, deux exemples. Pour chacun il est possible d'exiger des résultats avec plus de décimales. Problème posé par Gérard Crézé sur Tangente n°215
Résolution avec WolframAlpha (disponible en ligne)		Résolution avec Maple
Brèves associées	>>> Démonstration en géométrie		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Racines carrées >>> Identités remarquables >>> Système d'équations		>>> Ramanujan >>> Logiciel Maple >>> Théorème de Pythagore

1152. Carré différence de carrés
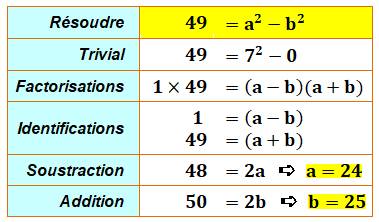
Énigme classique sur Internet et solution		Démystification Le fait que 49 soit un carré ou pas ne change rien. On exploite ici une relation générale qui dit que: Évidemment a et b ne seront des nombres entiers que si n est impair. Exemples 21 = 11² – 10² = 121 – 100 101 = 51² – 50² = 2601 – 2500
Propriété Tout nombre impair n est différence de deux carrés, l'un des nombres a est la moitié du nombre incrémenté de 1 et l'autre la moitié du nombre décrémenté de 1.
Brèves associées	>>> Cubes et carré de sommes de consécutifs		>>> Brèves Relations – Index
Pour en savoir plus	>>> Différences de carrés		>>> Carrés

1153. Énigmes arithmétiques
Quelle est la moitié de deux plus deux ?		1/2 de 2, plus 2 = 3 Mais 1/2 de (2+2) = 2 est tout aussi acceptable.
Quelle relation simple lie 2, 3, 4 et 5 ?		2 + 5 = 3 + 4
Calculer: 1/2 de 2/3 de 3/4 de 4/5 de 5/6 de 6/7 de 7/8 de 8/9 de 9/10 de 1000
Sept frères sont nés à deux ans d’intervalle. Le plus jeune a sept ans. Quel est l’âge du frère aîné ?		Sept frères mais six intervalles: 7 + 6 × 2 = 19 ans
Faire 1000 avec huit 8.		888 +88 + 8 + 8 + 8 = 1000
Dans deux ans, Tom aura deux fois l’âge qu’il avait il y a cinq ans. Quel âge a Tom ?		Si x est son âge. Dans deux ans : x + 2 et il y a cinq ans: x – 5. En égalant: (x + 2) = 2(x – 5) => x = 12 ans
Un couple a décidé d’organiser un pique-nique. Ils ont 5 fils et chaque fils a trois sœurs. Et chacune d’entre elles a un bébé. Combien d’individus sont allés au pique-nique ?		Couple: 2 (à ne pas oublier). Fils: 5 Sœurs : 3 (les mêmes pour chacun des frères) Bébé: 3 Total: 13
Dans une course, vous dépassez la personne en deuxième position. Quelle est alors votre nouvelle place ?		Vous avez pris la place du deuxième, alors vous êtes deuxième !
Trois nombres différents donnent la même somme que leur produit. Lesquels ?		1 + 2 + 3 = 1 × 2 × 3 On connait aussi: 2 + 2 = 2 × 2
Comment faire huit en ajoutant deux allumettes à trois allumettes ?		En formant le chiffre romain: VIII.
Brèves associées	>>> Énigme trompeuse		>>> Brèves Jeux – Index
Pour en savoir plus	>>> Énigmes virales sur Internet		>>> Énigmes et jeux – Index

1154. Triplet 3 5 7
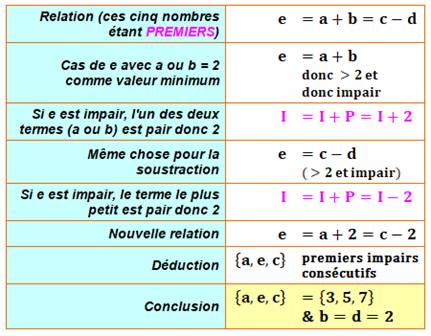
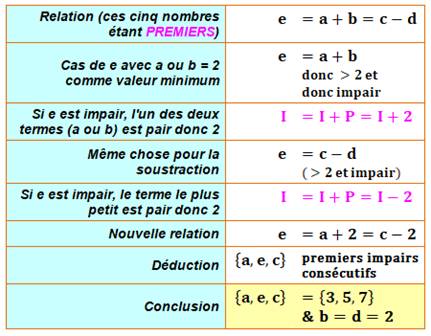
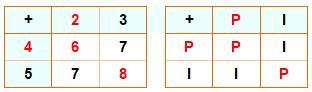
Propriété Le triplet {3, 5, 7} est le seul formé de trois nombres premiers impairs consécutifs. Occasion d'un beau raisonnement avec les pairs et les impairs en y ajoutant le fait que seul le nombre 2 est un nombre premier PAIR. Pairs et impairs Voyez cet exemple et la règle générale de l'addition des nombres selon qu'ils sont pairs (P) ou impairs (I): La même règle vaut pour les soustractions. Nombres premiers La liste commence par: 2, 3, 5, 7, 11, 13 … Seul 2 est un premier PAIR, tous les autres nombres premiers sont IMPAIRS.		Énigme Quels sont les cinq nombres PREMIERS tels que: e = a + b = c – d. Démonstration
Brèves associées	>>> Parité des puissances		>>> Brèves Théorie des Nbs – Index
Pour en savoir plus	Nombre 3 / Nombre 5 / Nombre 7 Triplet {3, 5, 7}		>>> Pairs et impairs >>> Nombres premiers

1155. Trois constantes rapprochées
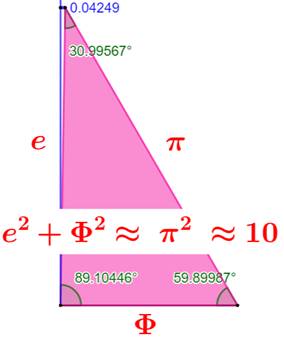
Triangle quasi-rectangle Le triangle ayant pour côtés les trois constantes e, Phi et Pi est quasiment un triangle rectangle. La relation du théorème de Pythagore est presque vérifiée. Le carré de Pi est proche de 10, comme l'est la somme des carrés de e et Phi. Comparaison
Brèves associées	>>> Carré et cubes – Belle égalité	>>> Brèves Relations – Index
Pour en savoir plus	>>> Constante e >>> Constante Pi	>>> Constante Phi (nombre d'or) >>> Constantes

1156. Cavalier et hypercube
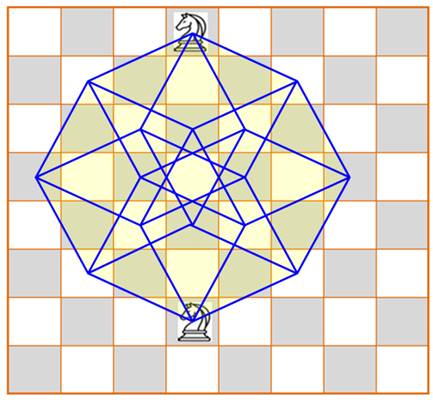
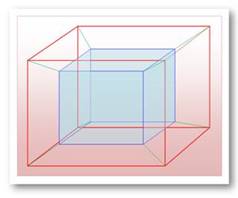
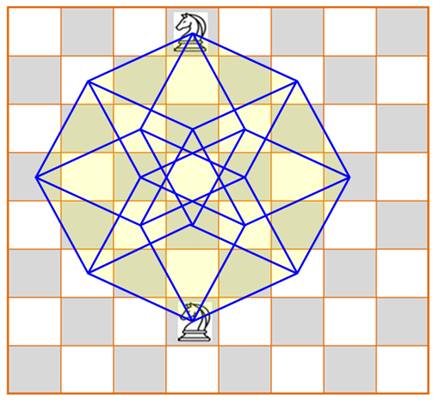
Les 24 (= 4!) trajets possibles du cavalier pour rejoindre la position six cases plus bas. C'est la représentation de l'hypercube.
Brèves associées	>>> Carré et cubes – Belle égalité		>>> Brèves Grilles – Index
Pour en savoir plus	>>> Déplacements du cavalier		>>> Hypercube

1157. Pépites numériques
Brèves associées		>>> Égalités surprenantes >>> pépites en trapèze	>>> Brèves Pépites – Index
Pour en savoir plus		>>> Pépites numériques	>>> Magie – Index

1158. Apprendre les multiplications
Table de Nicolas Chuquet (1145-1500) Cette table en triangle a l'avantage de ne présenter que les produits "utiles" car 3×7 = 7x3 par exemple. Apprentissage Notez qu'une fois connues les multiplications par 2, 3, 4 et 5, assez faciles à apprendre, il ne reste seulement que dix multiplications à connaitre. Les multiplications par 9 sont simples et on peut connaitre: 6×9, 7×9, 8×9 et 9×9. Reste six. Apprenez par cœur les carrés de 6, 7 et 8, il n'en reste plus que trois. Si vous notez que 56 = 7×8 (chiffres qui se suivent). Il en reste deux à apprendre par cœur: 6×7 et 6×8.
Brèves associées	>>> Multiplication mentale – le truc général		>>> Brèves Relations – Index
Pour en savoir plus	>>> Table de multiplications >>> Multiplication par 9		>>> Nombre 56 = 7×8 >>> Apprendre les carrés

1159. Racine de 5
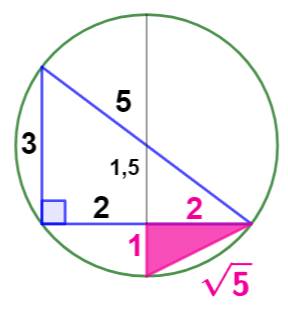
Construction Le triangle rectangle isiaque (3, 4, 5). Son cercle circonscrit. Le triangle rose de la figure. Son hypoténuse mesure racine de 5. Explications Les côtés mesurent 1 et 2. Le théorème de Pythagore donne: Pourquoi 1 pour le petit côté ? Ce segment fait partie du rayon du cercle qui vaut 5 / 2 = 2,5. Or, l'autre partie du segment est égal à la moitié du côté mesurant 3, soit 1,5 (théorème des points milieux). Alors: 2, 5 – 1, 5 = 1.
Brèves associées	>>> Nombre d'or et puissances		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Théorème des points milieux >>> Théorème de Pythagore		>>> Triangle isiaque >>> Racine de 5 = 2,236…

Retour	Brèves de maths – Page 57
Suite	Brèves de maths – Page 59
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve58.htm