NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/03/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	JEUX
Débutants Général	ÉNIGMES				Glossaire Général
INDEX JEUX	Classiques	Famille	Graphes	Villa
	Chapeaux	Truel	Chasseur	Pastis
		Sommaire de cette page >>> Eau et vin >>> L'eau dans le pastis >>> Analogie >>> Démonstration

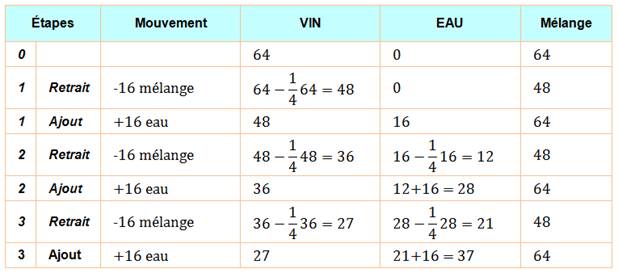
Mélanger l'eau au pastis

(ou eau et vin)

Résultat surprenant.

Devinettes

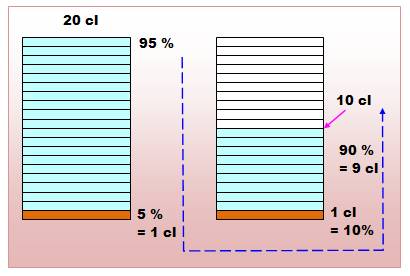
Un verre contient 20 cl de soda dont 95% d'eau. Il fait chaud, la boisson s'évapore et, il ne reste plus que 90% d'eau. Quelle est la quantité de boisson dans le verre ?

Ce matin, 100 kg de courges ont été mis au soleil. Ils étaient à 99% d'eau, mais tout au long de la journée, ils ont perdu de l'humidité par évaporation et maintenant ils ne sont plus qu'à 98% d'eau. Combien pèsent-ils maintenant?

Solution

EAU et VIN

Problème Un tonneau de 64 litres de vin. On tire 16 litres de vin que l'on remplace par 16 litres d'eau. On recommence l'opération: on tire 16 litres dans le tonneau et on rétablit le niveau en versant 16 litres d'eau. On reconduit l'opération une troisième fois. Combien reste-t-il de litres de vin dans le tonneau? Solution pas à pas Remarquons que 16 est le quart de 64. Solution en raisonnant Lors de la première opération, on retire un quart du vin. il en reste les trois quarts. On fait l'hypothèse que le vin et l'eau sont bien mélangés. Lors de deuxième, on retire un quart du mélange donc un quart du vin existant. Il en reste trois quarts des trois quarts. Pareillement pour la troisième opération, on retire un quart du mélange, donc un quart du vin existant. Il en reste trois quarts des trois quarts des trois quarts. En calculant cette valeur:

Cité par Tangente / Kangourou – Jan./fév. 2011

L'EAU DANS LE PASTIS – Question
Vin	Eau
Une mesure de pastis dans un verre.	Une cruche d'eau.
	On ajoute de l'eau dans le pastis.
C'est trop! Le pastis est noyé.
	On verse le trop plein dans la cruche.
Si bien que le contenu du verre revient au niveau de la mesure initiale.
Est-ce qu'il y a plus d'eau dans le pastis?	Ou plus de pastis dans l'eau?
Il y a autant de d'eau dans le pastis que de pastis dans l'eau

Narratif anglais / français (cas eau et vin)

The easiest way to explain this problem is, that if the volumes of liquid return to the exact same amounts, then, after the transfer of the wine and water, the wine that was transfered to the water has to be the same amount of water that was transfered to the wine. Or you could think about it this way: the amount of wine transfered to the water has to be the same amount of water transfered to the wine in order to keep both volumes of water the same in the end.

La façon la plus simple d'expliquer ce problème est la suivante : si les volumes de liquide reviennent exactement aux mêmes quantités, alors, après le transfert du vin et de l'eau, le vin qui a été transféré à l'eau doit être la même quantité d'eau qui a été transférée au vin. Ou encore, on peut raisonner de la façon suivante : la quantité de vin transférée à l'eau doit être la même que la quantité d'eau transférée au vin pour que les deux volumes d'eau restent identiques au final.

Voir Anglais pour le bac et pour les affaires

Analogie pour vous convaincre
Panier gauche Boules noires	Panier droit Boules rouges
50	500
Transfert de 100 rouges dans le panier des noires.
50 + 100	400
Transferts de 100 boules du panier gauche vers le panier droit Disons 30 noires et 70 rouges
50 – 30 + 100 – 70 20 + 30 = 50	30 + 400 + 70 30 + 470 = 500
Bilan
30 rouges dans le panier des noires	30 noires dans le panier des rouges

Démonstration
Panier gauche Boules noires	Panier droit Boules rouges
N	R
r boules rouges de droite vers gauche.
N + r	R - r
n boules noires et r' boules rouges de gauche vers droite.
N - n + r - r'	n + R - r + r'
Or il y a même contenance au départ et à l'arrivée.
N = N - n + r - r' n = r - r'
n est le nombre balles noires dans le panier droit.	r est la quantité de boules rouges versées dans le panier gauche. r' est celle qui sont revenues dans le panier droit. r - r' est la quantité de boules rouges finalement dans le panier de gauche.
Quantité de noires à droite	= quantité de rouges à gauche.

Devinette – Solution

Énigme

Un verre contient 20 cl de soda dont 95% d'eau. Il fait chaud, la boisson s'évapore et, il ne reste plus que 90% d'eau. Quelle est la quantité de boisson dans le verre?

Solution

Ce qui n'est pas de l'eau constitue la partie constante du mélange: elle n'est pas soumise à l'évaporation.

Cette partie représente 100 – 9 5 = 5% de 20 cl, soit 1cl.

Après évaporation, il représente: 100 – 90 = 10% du volume final.

Si 1 cl = 10%, alors le volume total vaut: 10 cl.

Solution express

95 % d'eau dans 20 cl, reste 5% sans eau = 1 cl

La nouvelle concentration donne un volume égal à: V = 1 + 0,9 V

Calcul de V = 1 / (1 – 0,9) = 1 / 0,1 = 10 cl.

Cas des courges

99 % d'humidité pour 100 kg, reste 1% de matière, soit 1kg.

Le poids en fin de journée: P = 1 + 0,98 P

Calcul de P = 1 / (1 – 0,98) = 1 / 0,02 = 50 kg

Retour

Suite	Voir haut de page
Famille	Anniversaires Autres énigmes sur les âges Dates de naissance produit Élections Énigmes des filles Énigmes famille et probabilités Famille et probabilités Filles (les trois) Garçons & Filles Huit fois mon âge Paradoxes Roméo et Juliette
Voir	Jeux – Index Logique – Index
Cette page	http://villemin.gerard.free.fr/Puzzle/Pastis.htm