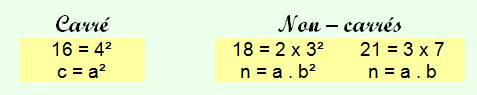|
||||||||||||||||||||||||||||||||
![]()
|
CARRÉS & NON - CARRÉS Comment
caractériser un nombre qui est un carré parfait ou non? But:
disposer d'une représentation utile pour effectuer des démonstrations.
|
|
|
||
|
On peut utiliser la définition du
carré: Le carré d'un nombre est égal au
produit du nombre par lui-même. Cette définition est valable que le
nombre soit un nombre premier
ou un nombre composé. |
n = a . a = a2 |
|
|
S'il est composé, le nombre peut s'écrire sous la forme de ses
facteurs premiers |
a = p1E1
. p2E2 . ... pmEm |
|
|
Et c'est toute cette expression qui
est au carré Autrement dit, on peut aussi écrire: |
n = a2
= (p1E1 . p2E2 . ... pmEm) 2 n = a2 = p12xE1
. p22xE2 . ... pm2xEm |
|
|
Prenant sa
décomposition en facteurs premiers, un carré est un nombre dont tous les exposants sont pairs. |
n = a2 = p12xE1
. p22xE2 . ... pm2xEm |
|
|
|
|||
|
Comment représenter un nombre qui
n'est pas un carré? À partir de la conclusion ci-dessus,
la conclusion est pratiquement évidente |
|||
|
Prenant sa décomposition en facteurs
premiers, pour qu'un nombre soit non-carré il suffit que l'un des
exposants soit impair. On se souvient qu'un nombre impair est représenté par 2k + 1. |
n =
p12xE1 .
p22xE2 . ...
. pi2xEi
+ 1 . ...
. pm2xEm |
||
|
On peut aussi écrire, en isolant le
facteur particulier. B étant le produit de tous les autres facteurs premiers. On note que, bien sûr, pi
étant premier différent des autres, il ne peut pas diviser B. |
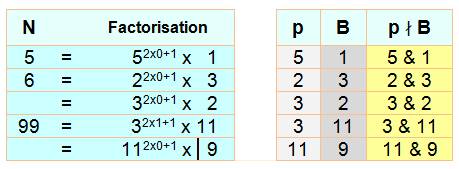
n = pi2xEi+1 .
B avec pi |
||
|
Exemples |
|
||
Note: Le symbole "ne divise pas"
est une barre verticale barrée;
|
Cette représentation sert dans la démonstration
de l'irrationalité de |
Voir Racine de 2 est irrationnel
![]()
|
Suite Retour |
|||||||||||||||||||||||||||
|
Carrés |
|
||||||||||||||||||||||||||
|
Voir |
|
||||||||||||||||||||||||||
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/Carre.htm |
![]()