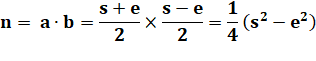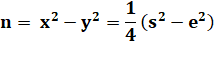|
||||||||||||||||||||||||||||||||||||||||
![]()
|
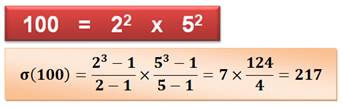
SOMME des DIVISEURS Nombres SOMME de PUISSANCES Méthode de calcul de la somme des diviseurs à partir de la somme des
puissances des nombres. Comment retrouver le nombre n connaissant la somme de ses diviseurs. Exemple: s = 224, il faut retrouver n = 84. |
|
|
||
|
Calcul
direct de la somme des diviseurs |
Div(100) = {1, 2, 4, 5, 10, 20, 25, 50, 100} Somme: 217 |
|
|
Formule de calcul de la somme des diviseurs. |
|
|
|
Méthode
particulière Voyez ce
produit et son développement qui redonne bien la liste des diviseurs. |
S = (20 + 21 + 22) (50 + 51
+ 52) = 1 + 2 + 4 + 5 + 10 + 50 + 4
+ 20 + 100 |
|
|
Observation Somme diviseurs = produit de la somme des
puissances de chaque facteur jusqu'à la valeur de l'exposant. |
S = somme des puissances de 2 jusqu'à 2 S = 7 x 31 |
|
|
Exemple avec 1800 = 23 x 32 x 52 Diviseurs de 1800: {1, 2, 3, 4, 5, 6, 8, 9, 10,
12, 15, 18, 20, 24, 25, 30, 36, 40, 45, 50, 60, 72, 75, 90, 100, 120, 150,
180, 200, 225, 300, 360, 450, 600, 900, 1800} |
S = (1 + 2 + 4 + 8) (1 + 3 + 9) (1 + 5 + 25) = 15
x 13 x 31 = 6 045 |
|
|
|
||
|
Toute
somme de diviseurs est un produit de
sommes de puissances. Table des sommes de puissances à droite. On y
retrouve les facteurs du produit 6 045 somme des diviseurs de 1 800. |
Exposant, [valeurs successives des sommes avec
cette puissance] 2, [1, 3, 7, 15, 31, 63, 127, 255,
511] 3, [1, 4, 13, 40, 121, 364] 5, [1, 6, 31, 156, 781] 7, [1, 8, 57, 400] 11, [1, 12, 133] 13, [1, 14, 183] 17, [1, 18, 307] 19, [1, 20, 381] 31, [1, 32, 993] 37, [1, 38] |
|
|
|
||
|
Comment
calculer le nombre connaissant la somme ? |
S = 112 => n = ? |
|
|
Factorisation
de la somme s jusqu'à trouver des nombres qui figurent dans la table |
S = 2 x 56 = 4 x 28 = 8 x 14 |
|
|
Transcription
de ces nombres selon leur place dans la table |
7, [1, 8, 57, 400] => 71 13, [1, 14, 183] => 131 |
|
|
Nombre = produit des valeurs trouvées |
n = 71
x 131 = 91 |
|
|
Vérification |
Div(91) = {1, 7, 13, 91} S = 1 + 7 + 13 + 91 = 112 |
|
|
Autre exemple |
s = 91 => n = ? s = 7 x 13 n = 22 x 32 = 36 |
|
Autre |
s = 224 => n = ? s = 2 x 112 = 4 x 56 = 4 x 8 x 7 OK n = 31 x 71 x 22 = 84 |
|
Cas du
nombre s = 12 Une somme
peut correspondre à plusieurs nombres. |
s = 12 => n = ? s = 1 x 12 OK s = 2 x 6 = 3 x 4 OK Soit deux possibilités: n = 1k x 111 = 11 n = 21 x 31 = 6 |
Sommes et nombres correspondants pour somme jusqu'à 110
En couleur, les cas de plusieurs nombres pour une somme
donnée
|
[1, 1], [3, 2], [4, 3], [6, 5], [7, 4], [8, 7], [12, 6], [12,
11], [13, 9], [14, 13], [15, 8], [18, 10],
[18, 17], [20, 19], [24, 14], [24,
15], [24, 23], [28, 12], [30, 29], [31, 16], [31,
25], [32, 21], [32,
31], [36, 22], [38, 37], [39, 18], [40, 27], [42,
20], [42, 26], [42,
41], [44, 43], [48, 33], [48, 35], [48,
47], [54, 34], [54,
53], [56, 28], [56,
39], [57, 49], [60, 24], [60, 38], [60,
59], [62, 61], [63, 32], [68, 67], [72,
30], [72, 46], [72,
51], [72, 55], [72,
71], [74, 73], [78, 45], [80, 57], [80, 79], [84,
44], [84, 65], [84,
83], [90, 40], [90,
58], [90, 89], [91, 36], [93, 50], [96, 42], [96,
62], [96, 69], [96,
77], [98, 52], [98, 97], [102, 101], [104,
63], [104, 103], [108,
85], [108, 107], [110, 109] |
Plus
petits nombres qui sont k fois sommes des diviseurs de nombres
|
11, 122, 243,
964, 725, 168, 240, 336, 360, 50410, 576,
1512, 1080, 1008, 720, 2304, 3600, 5376, 2520, 216020, 1440,
10416, 13392, 3360, 4032, 3024, 7056, 6720, 2880, 6480, 10800, 13104, 5040, 6048,
4320, 13440, 5760, 18720, 20736, 19152, 22680, 43680, … |
|
Liste des
nombres ayant la même somme de diviseurs pour k record 1, 1, [1] 2, 12, [6,
11] Le nombre 12
est deux fois somme de diviseurs pour 6 et 11. 3, 24, [14, 15, 23] 4, 96, [42, 62, 69, 77] 5, 72, [30, 46, 51, 55, 71] 6, 168, [60, 78, 92, 123,
143, 167] 7, 240, [114, 135, 158, 177,
203, 209, 239] 8, 336, [132, 140, 182, 188,
195, 249, 287, 299] 9, 360, [120, 174, 184, 190,
267, 295, 319, 323, 359] 10, 504,
[204, 220, 224, 246, 284, 286, 334, 415, 451, 503] 11, 576,
[210, 282, 310, 322, 345, 357, 382, 385, 497, 517, 527] 12, 1512, [480, 636, 736,
748, 830, 902, 1006, 1105, 1255, 1391, 1411, 1511] 13, 1080, [408, 440, 534,
568, 590, 638, 646, 718, 807, 895, 979, 1003, 1007] 14, 1008, [390, 460, 476,
498, 574, 598, 615, 663, 715, 753, 835, 913, 923, 943] 15, 720, [264, 270, 280,
354, 376, 406, 418, 435, 459, 478, 537, 623, 649, 667, 719] 16, 2304, [930, 966, 1146,
1155, 1270, 1426, 1491, 1551, 1581, 1645, 1705, 1771, 1915, 2101, 2159, 2201] 17, 3600, [1080, 1416, 1566,
1624, 1672, 1912, 1990, 2086, 2235, 2242, 2403, 2755, 2995, 3143, 3383, 3401,
3427] 18, 5376, [1860, 1932, 2292,
2418, 2540, 2852, 3003, 3122, 3302, 3345, 3507, 3813, 4277, 4433, 4979, 5129,
5177, 5207] 19, 2520, [864, 984, 1068, 1144,
1180, 1276, 1292, 1336, 1390, 1436, 1534, 1558, 1678, 1885, 2095, 2327, 2363,
2407, 2419] 20, 2160, [870, 918, 920,
952, 1074, 1246, 1298, 1334, 1335, 1431, 1438, 1479, 1595, 1615, 1795, 1883,
1969, 2033, 2047, 2059] 21, 1440, [552, 570, 594,
616, 790, 826, 874, 885, 957, 958, 969, 1015, 1045, 1077, 1195, 1253, 1343,
1349, 1357, 1363, 1439] 21, 10416, [3120, 3300,
3660, 3984, 4550, 4592, 4700, 4758, 4784, 5612, 5948, 6062, 6225, 6495, 7175,
7475, 7503, 8723, 9107, 9659, 9959] 18, 13392, [4080, 5136, 5680,
5936, 5950, 6222, 6256, 6710, 6896, 7430, 7798, 8025, 8355, 8662, 8926, 9275,
9699, 9775] 24, 3360, [1140, 1188, 1482,
1580, 1652, 1748, 1755, 1784, 1916, 1946, 2054, 2085, 2241, 2301, 2337, 2517,
2639, 2717, 2933, 3107, 3173, 3197, 3239, 3359] 25, 4032, [1380, 1428, 1540,
1722, 1794, 1988, 2002, 2068, 2108, 2145, 2230, 2338, 2505, 2542, 2739, 2769,
2829, 2905, 3055, 3157, 3289, 3521, 3791, 3841, 3901] |
Sommes de diviseurs possibles (310 valeurs sur 1000 nombres)
Nombres produits de sommes de puissances
|
1, 3, 4, 6, 7, 8, 12, 13,
14, 15, 18, 20, 24, 28, 30, 31, 32, 36, 38, 39, 40, 42, 44, 48, 54, 56, 57,
60, 62, 63, 68, 72, 74, 78, 80, 84, 90, 91, 93, 96, 98, 102, 104, 108, 110,
112, 114, 120, 121, 124, 126, 127, 128, 132, 133, 138, 140, 144, 150, 152,
156, 158, 160, 162, 164, 168, 171, 174, 176, 180, 182, 183, 186, 192, 194,
195, 198, 200, 204, 210, 212, 216, 217, 222, 224, 228, 230, 234, 240, 242,
248, 252, 255, 256, 258, 260, 264, 266, 270, 272, 278, 280, 282, 284, 288,
294, 296, 300, 304, 306, 307, 308, 312, 314, 318, 320, 324, 330, 332, 336,
338, 342, 348, 350, 352, 354, 360, 363, 364, 368, 372, 374, 378, 380, 381,
384, 390, 392, 396, 398, 399, 400, 402, 403, 408, 410, 414, 416, 420, 422,
432, 434, 440, 444, 448, 450, 456, 458, 462, 464, 465, 468, 474, 476, 480,
488, 492, 494, 496, 500, 504, 508, 510, 511, 512, 518, 522, 524, 528, 532,
540, 542, 544, 546, 548, 549, 552, 553, 558, 560, 564, 570, 572, 576, 578,
582, 588, 592, 594, 600, 602, 608, 612, 614, 616, 618, 620, 624, 630, 632,
636, 640, 642, 644, 648, 654, 656, 660, 662, 672, 674, 678, 684, 686, 690,
692, 696, 702, 710, 714, 720, 726, 728, 732, 734, 740, 741, 744, 752, 756,
758, 760, 762, 768, 770, 774, 776, 780, 781, 784, 788, 792, 798, 800, 806,
810, 812, 816, 819, 822, 824, 828, 830, 832, 834, 840, 846, 847, 848, 852,
854, 855, 858, 860, 864, 868, 871, 878, 880, 882, 884, 888, 896, 900, 908,
912, 920, 921, 924, 930, 931, 936, 938, 942, 948, 952, 954, 960, 961, 962,
966, 968, 972, 978, 980, 984, 992, 993, 996, 998, … |
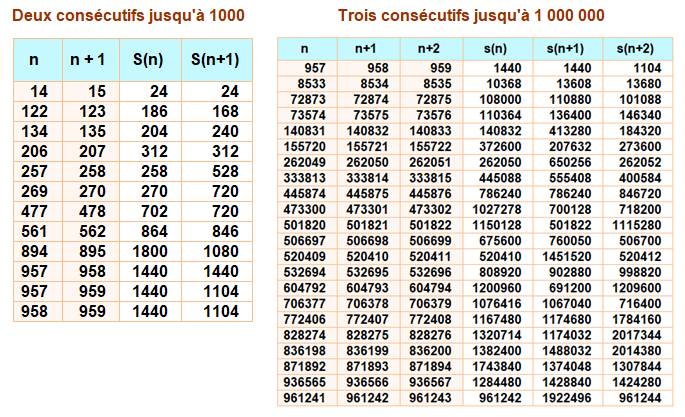
Nombres successifs avec mêmes chiffres dans
la somme de leurs diviseurs
|
Exemple Les
nombres 122 et 123 ont 186 et 168 pour somme des diviseurs. Ce sont les mêmes
chiffres {1, 6, 8}.
Exemple avec
le dernier cas du tableau de droite
|
Voir Sommes identiques /
Nombre 14 / Nombre 122
/ Nombre
957 / Nombre
961 241
![]()
Exercice
|
|
||||||||
|
Soit un
nombre composé à deux facteurs. On
souhaite connaitre la somme et la différence des facteurs sans passer par la
factorisation. Possible ? |
Exemple
Connaissant n = 21, trouver s = 10 et e = 4 |
|||||||
|
|
|
|||||||
|
Si on
connait s et e, on reconstruit le nombre et ses facteurs. |
Exemple
|
|||||||
|
On se
demande, connaissant n, s'il est possible de connaitre s et e sans connaitre
a et b. Exploitation
de produits, différences de carrés. |
|
|
|
Tout nombre,
sauf quelques uns, sont différence
de deux carrés. |
n = x² – y² = (x + y)
(x – y) |
|
|
En
rapprochant: Connaissant
x et y, peut-on trouver s et e ? |
|
|
|
Exemple avec n
= 21 Si on
sait trouver son expression comme différence de deux carrés. |
21 = x² – y² = 11² – 10² = 5² – 2² |
|
|
Note: pour
trouver ces différences de carré on s'appuie généralement sur la factorisation
de n. Si le nombre est impair (n =
2k +1), il est la différence de deux carrés successifs: n = (k+1)² - k². Ex:
91 = 45x2 + 1 = 46² - 45². |
21 = 7 x 3 = (5 + 2)
(5 – 2) = 5² – 2² |
|
|
Les
valeurs de s et e sont doubles. |
(s, e) = (22,
20) ou (10, 4) |
|
|
On lève
le doute par le calcul de a et b, puis le calcul de n. |
(a, b) = (21, 1) ou (7, 3) n
= 21 ou 21 => BON |
|
|
Bilan: on sait calculer
s et e à partir de n; oui, mais … |
À condition de connaitre la décomposition de n en
différences de carrés (ce qui n'est pas toujours possible). Ce qui revient généralement à … trouver les
facteurs de n ! |
|
|
Attention Exemple
avec 100 |
100² = 26² – 24² seule
différence possible (a, b) = (50, 2) et 50
x 2= 100 Bien ! Mais, ce procédé n'a détecté qu'une des
factorisations de 100. |
|
Voir Brève
562
![]()
|
Retour Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/DivSomm1.htm
|
![]()