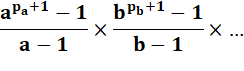|
||||||||||||||||||||||||||||||||||||
![]()
|
CALCUL AVEC LES DIVISEURS Trouver
la quantité ou la somme des diviseurs. Un bref
aperçu. Voir développements >>> |
|
|
||
|
La quantité de diviseurs de N = ap
. bq . cr ... est |
||
|
Démonstration ap est divisible par 1,
a, a2, ... ap N est divisible
par (1, a, a2, ... ap)(1,
b, b2, ... bp)(1, c, c2, ... cp)(... Soit: (p+1) facteurs fois (q+1)
facteurs, etc. |
Exemple 32 x 51
= 45 Nombre
de diviseurs = (2 + 1) (1 + 1) = 6 En effet, (1
x 3 x 9) (1 x 5) = 1 x 3 x 9 x 5 x 15 x 45 |
|
Voir Calcul
des diviseurs propres
|
|
||
|
N ayant n
facteurs premiers différents, la quantité de produits de deux facteurs
premiers entre eux est 2n - 1 . |
45
= 32 x 5 Quantité
de produits : 2 (2-1) = 2 En effet, 3 et 5 sont les deux seuls facteurs
premiers de 45 |
|
|
|
||
|
Somme des diviseurs =
|
21 600 = 63 . 102 = 23 . 33 . 25 . 52
= 25 . 33 . 52 Quantité de diviseurs : (5 + 1) (3 + 1) (2 + 1) = 72 Somme des diviseurs : (26 – 1)/(2 – 1) . (34 – 1 )/(3 –
1) . (53 - 1)/(5 – 1) = 63 x 40 x 31 = 78 120 Quantité de produits de deux facteurs
premiers entre eux avec 3 facteurs différents 2(3 – 1) = 4 |
|
![]()
Amusements et curiosités
|
|
||||
|
Nombre
dont le plus grand facteur est égal à la
somme des chiffres du nombre. |
Exemples 12 = 2 x 3 & 3 = 1 +
2 1729 = 7 x 13 x 19 & 19 = 1 + 7 + 2 + 9 |
|||
|
Liste pour n de 2 à 1000 2, {2} 3, {3} 5, {5} 7, {7} 12, {2, 3} 50, {2, 5} 70, {2, 5, 7} |
308, {2, 7, 11} 320, {2, 5} 364, {2, 7, 13} 476, {2, 7, 17} 500, {2, 5} 605, {5, 11} 700, {2, 5, 7} 704, {2, 11} 715, {5, 11, 13} 832, {2, 13} 935, {5, 11, 17} |
1088, {2, 17} 1183, {7, 13} 1547, {7, 13, 17} 1729, {7, 13, 19} 2401, {7} 2584, {2, 17, 19} 2618, {2, 7, 11,
17} 2704, {2, 13} 2926, {2, 7, 11,
19} |
3080, {2, 5, 7, 11} 3200, {2, 5} 3536, {2, 13, 17} 3640, {2, 5, 7, 13} 3952, {2, 13, 19} 4225, {5, 13} 4760, {2, 5, 7, 17} 4784, {2, 13, 23} 4913, {17} 5000, {2, 5} |
|
Voir Nombres de Ruth-Aaron
(sommes de facteurs égales)
|
|
||
|
Nombre
dont la somme des facteurs est égal à la
somme des chiffres du nombre. Note: les
nombres
parfaits sont ceux dont la somme des diviseurs propres est gale au
nombre. Il se trouve que les diviseurs propres de 6 (1, 2 et 3) sont aussi ses
facteurs premiers. Alors que pour 28, le nombre parfait suivant, ce n'est pas le cas: 28 = 2 x 2 x 7 => somme 11 Sigma'(28) = {1, 2, 4, 7, 14} = 28 |
Tous les nombres premiers sont dans ce cas: 13 = 1 x 13 si on ignore
le facteur 1. Sinon le plus petit tel nombre est 6 6 = 1 x 2 x 3 & la somme vaut 1 + 2 + 3 = 6. Et, on montre facilement que c'est le seul cas. Le cas critique
correspond à 2 x k = N; or k est moitié de N et en y ajoutant 2, on
n'atteindra jamais N. |
|
![]()
|
Suite plus
formelle |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
|
![]()