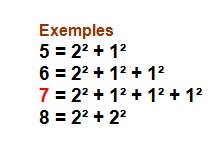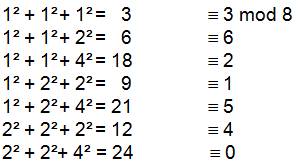|
|||||||||||||||||||||||||||||||
![]()
|
SOMME de TROIS CARRÉS Problème plus difficile que pour deux ou
quatre.
|
Voir Cas de ces trois carrés: x² + y² + 1²
|
|
|||
|
Théorème énoncé par Fermat - 1636 et 1658 Un nombre est somme de trois carrés
si et seulement s'il N'est PAS de cette
forme (h et k entiers positifs) Un nombre de cette forme exige 4 carrés. Démonstration La démonstration complète dépasse le
cadre de ce site. |
n = 4h (8k + 7) |
||
|
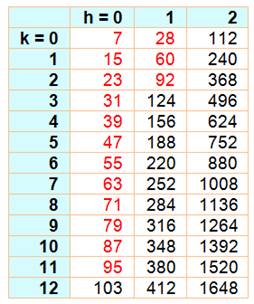
Nombres de la forme n = 4h (8k + 7)
|
Nombres somme de trois carrés jusqu'à 100
Les quinze nombres manquants dans
cette liste sont tous dans le tableau de gauche (rouge). |
||
|
|
|||
|
Théorème Tout nombre congruent à 7 mod 8 n'est
jamais somme de 3 carrés. Autrement
dit Tout nombre dont la division par 8 donne
un reste de 7 n'est jamais somme de 3 carrés. |
Si
n n n'est
pas somme de 3
carrés |
||
|
Démonstration Supposons que la somme des trois
carrés est congruente à 7 mod 8. |
n n a² + b² + c² |
= 7 mod 8 = a² + b² + c² = 7 mod 8 |
|
|
Remarquons tout de suite que, le
reste de la division de n par 8 étant 7, le nombre n n'est pas
pair. |
n |
est impair |
|
|
n est impair et somme de trois
nombres,
|
P+P+P P+P+I P+I+I I+I+I |
= P = I = P = I |
|
|
On ne perd pas en généralité en
disant que a est l'impair. |
a² |
est impair |
|
|
Propriété de chaque
carré modulo 8
|
a² b² c² |
= 1 mod 8 = { 0, 1, 4 } mod 8 = { 0, 1, 4 } mod 8 |
|
|
Dans le cas où a, b et c sont
impairs. En calculant la somme. La somme n'est pas égale à 7 mod 8
(hypothèse)
|
a² b² c² a² + b² + c² |
= 1 mod 8 = 1 mod 8 = 1 mod 8 = 3 mod 8 |
|
|
Dans le cas où a est impair, et b et c sont pairs En calculant la somme. La somme n'est pas égale à 7 mod 8
(hypothèse)
|
a² b² c² a² + b² + c² |
= 1 mod 8 = { 0, 4 } mod 8 = { 0, 4 } mod 8 = {1, 4, 9
} mod 8 = {1, 4 }
mod 8 |
|
|
En aucun cas nous ne trouvons la
valeur 7 imposée par l'hypothèse. |
Si n Alors n |
= 7 mod 8 ¹ a² + b² + c² |
|
|
NB: La somme des carrés modulo 8 est
égale à 3, 1 ou 4. Il faut se garder de conclure
qu'elle n'est jamais égale à 0, 2, 5, 6, 7. En effet, l'hypothèse du 7 a été
faite et, elle a servi au cours de la démonstration Contre
exemple => |
|
|
|
||
|
Quelques résultats Selon la forme de n, la
quantité q de présentations en somme de 3 carrés. La formule générale n'est pas simple
! Pour un
panorama en anglais: Sum of squares
function |
q( 8k + 7
) = 0 q( 4n ) =
q (n) |
|
|
|
|
|
Fermat en 1636: aucun nombre en 8k
+ 7 n'est somme de 3 carrés. Il complète en 1658 et formule le théorème
sans le démontrer. La démonstration est de Legendre –
Essai sur la théorie des nombres – 1798 et aussi Gauss- Disquistiones
Arithmeticae – 1801. Elle fait intervenir la théorie des résidus
quadratiques. Liouville and Uspensky ont développé
une alternative plus simple, mais longue – Elementary Number Theory – 1939. |
|
Partition de carrés en carrés?
|
Tout
nombre carré pair est la somme de quatre
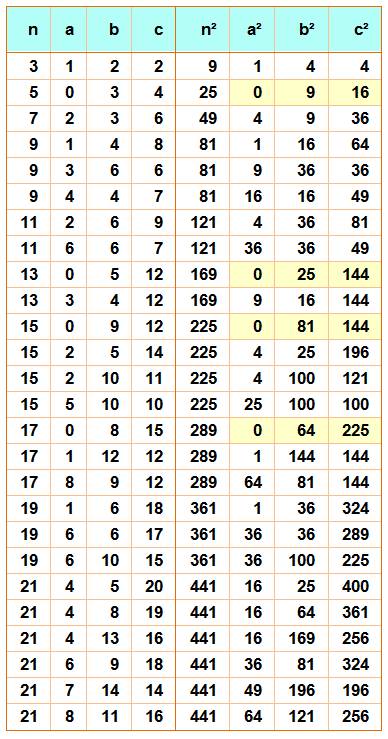
carrés identiques; Tout nombre carré impair est somme d'au plus trois carrés différents. Un
carré somme de deux carrés forme un triplet de Pythagore. Nombre pair:
(2k)² = 4k² = k² + k² + k² + k². Nombre impairs: (2k + 1)² = 4k² + 4k + 1 (conclusion moins évidente) À partir de 9, les
carrés des nombres impairs sont plusieurs fois somme de trois carrés.
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/SomCa3ca.htm
|
![]()