NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 17/05/2021

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

      

Théorie des Nombres

 

Débutants

Division

Fonctions

ARITHMÉTIQUES

 

Glossaire

Division

 

 

INDEX

 

Accueil

 

Sommaire

Liste des fonctions

Diviseurs

Lambda

Moebius / Mertens

 

Sommaire de cette page

>>> Fonction lambda de Liouville

>>> Graphe

>>> Propriétés

>>> Comportement

>>> Programmation

 

 

 

 

 

Fonction lambda de n

 

Fonction arithmétique introduite par Liouville qui caractérise la parité de la quantité des facteurs premiers d'un nombre.

 

Utile pour l'étude des fonctions multiplicatives et indirectement pour la résolution de la conjecture des écarts d'Erdös par Terence Tao.

 

 

 

 

Fonction de Liouville: lambda de n

 

Oméga de n

Donne la quantité de facteurs premiers d'un nombre, y compris leur répétition.

 

n = 10 = 2 x 5

n = 100 = 2² x 5²

 

 

Lambda de n

 

 

Cette fonction vaut 1 si la quantité de facteurs est paire et -1 sinon.

 

L(n)

 

Fonction de Liouville

C'est la somme de 1 à n des valeurs de lambda (n).

Exemples

n = 2 

n = 10 = 2 x 5

n = 100 = 2² x 5²

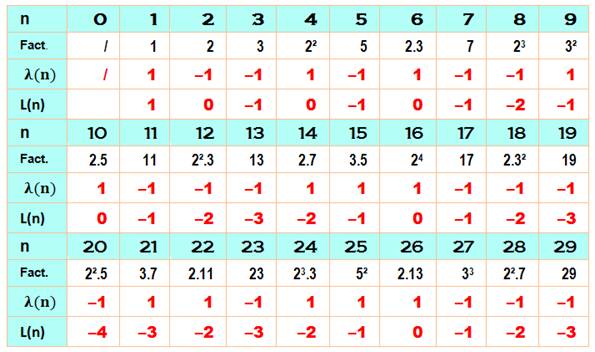
Valeurs

 

Graphe

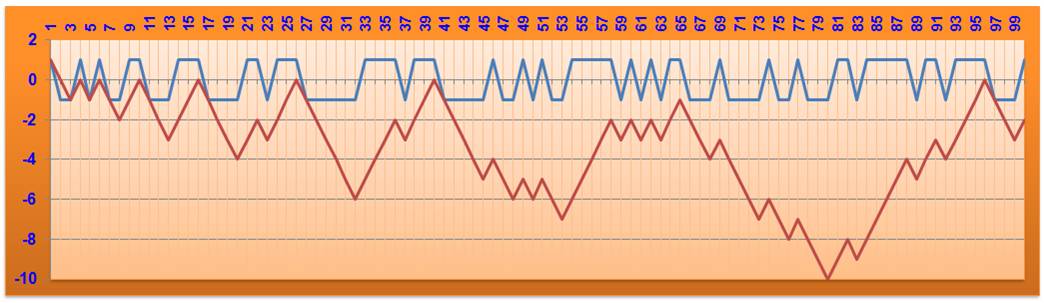
Lambda en bleu et L en marron

 

Fonction de Liouville nulle

 

Pour n de 1  à 12

n

Ω

λ

Σλ

1

 0

 1

 1

2

 1

 -1

 0

3

 1

 -1

 -1

4

 2

 1

 0

5

 1

 -1

 -1

6

 2

 1

 0

7

 1

 -1

 -1

8

 3

 -1

 -2

9

 2

 1

 -1

10

 2

 1

 0

11

 1

 -1

 -1

12

 3

 -1

 -2

  

 

Valeur de n pour cumul de la fonction de Liouville passe par 0

2, 4, 6, 10, 16, 26, 40, 96, 586, 906 150 256, 906 150 294, 906 150 308,…

A028488

 

Valeurs record

[1, 1], [8, -2], [13, -3], [20, -4], [31, -5], [32, -6], [53, -7], [76, -8], [79, -9], [80, -10], [117, -11], [176, -12], [181, -13], [182, -14], [193, -15], [200, -16], [283, -17], [284, -18], [285, -19], [286, -20], [293, -21], [440, -22], [443, -23], [468, -24], [661, -25], [678, -26], [683, -27], [684, -28], …

 

 

Propriétés

Propriété multiplicative

La fonction oméga (n) est additive et par conséquent la fonction lambda (n) est multiplicative.

Voir Application des fonctions multiplicatives

Conjecture

On a pensé (conjecture de Polya) que la somme L(n) des valeurs de lambda de 1 à n était négative ou nulle.

Un contre exemple fut trouvé en 1980 avec n = 906 150 257 pour lequel la somme vaut 1.

Signes

La quantité de changements de signe le long de la séquence de 1 et -1 est liée à l'hypothèse de Riemann

 

 

On ignore si la quantité de changement de signe est infinie.

Premiers

La fonction de Liouville donne un moyen de calculer la quantité de nombres premiers jusqu'à un nombre donné. Fonction pi(n)

 

 

Comportement

 

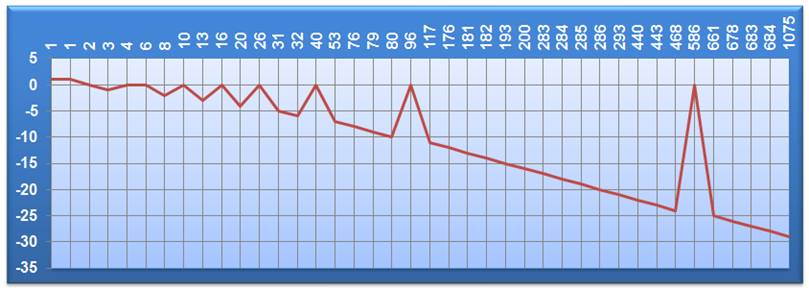
Ce graphe indique les points pour lesquels la fonction de Liouville (L):

*    détient un record en négatif: pour n = 80, L = -10 alors que pour n = 53, L = -7;

*    remonte à la valeur 0: pour n = 96 L = 0. La prochaine occurrence est pour n = 586.

 

 

L'allure de cette courbe se prolonge: avec n croissant:

*    la descente de L est de plus en plus profonde. Par exemple, pour n = 423 920 456, elle atteint -20 000; et,

*    la plage entre deux L = 0 est de plus en plus grande, sans jamais revenir à 1. Après n = 586, le prochain passage à 0, intervient pour n > 1 000 000.

  

 

 

Programmation Maple

 

Rappel sur l'extraction des facteurs et leur décompte

 

 

nf: = ifactors(72):

Extraction des facteurs du nombre 72 (exemple) dans nf.

nf;

Impression de nf. Ici: 72 = 23 x 32

Comment extraire la quantité des facteurs

nf[2];

        

Extraction du 2e terme.

nf[2][1];

           

Extraction de son 1er terme.

nf[2][1][2];

               3

Extraction de son 2e terme.

nops(nf[2]));

2

Donne la quantité de facteurs distincts.

Comment compter les facteurs

F:= add(nf[2][i][2], i = 1..nops(nf[2]));

Addition des quantités de facteurs répétés pour i allant de 1 à la quantité de facteurs distincts.

 

Programme complet

 

Ouverture du package théorie des nombres.

Mise à zéro; redémarrage.

 

 

Procédure de calcul de la valeur de lambda (n). En utilisant l'instruction expliquée ci-dessus.

 

 

 

 

 

 

 

 

Liste A pour les valeurs de lambda.

Liste L pour les fonctions de Liouville.

 

Exemple pour le calcul des dix premières valeurs.

Attention: bien spécifier un départ à i = 1 et non pas à 0.

On place lambda (n) dans l.

On ajoute l à la liste A.

On calcule la somme S, que l'on ajoute à la liste L

 

 

Impression des listes A et L.

Voir Quantité de diviseurs – Maple (explications pas à pas)

 

 

 

Programme donnant le passage à 0 de la fonction de Liouville

utilisant l'instruction de calcul des sommes cumulées (PartialSums)

Programmes de Robert Israel - A028488  

 

Voir Programmation – Index

 

 

 

Suite

*         Quantité de facteurs premiers

Autour

*         Fonctions de Moebius  et de Mertens

Voir

*         Cryptage

*         Des jeux sur les partages

*         Jeux et puzzles – Index

*         L'arithmétique de l'horloger – Congruence / Modulo

*         Le calcul mental

*         Théorie des nombres – Index

Site

*         Liouville function – Wolfram MathWorld

*         Liste des valeurs en OEIS A 008836

Cette page

http://villemin.gerard.free.fr/Referenc/Prof/THdesNBS/Lambda.htm