NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/12/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TECHNOLOGIE
Débutants Général	Nanotechnologies		Glossaire Général
INDEX Sciences	Approche	Gravure
	Sommaire de cette page >>> Approche >>> Tailles comparées >>> Données >>> Nanoparticules >>> Historique >>> Danger ? >>> Nanoparticules dans la nature >>> Granularité et surface développée

Un monde de l'infiniment petit où les cheveux sont des câbles géants, cent mille fois plus gros que la magnifique sphère de carbone, exhibée par Kroto. Étonnant spectacle de l'invisible sur scène, de la science en marche avec son panache de fascination.

Dorothée Benoit Browaeys - Allusion à la présentation du fullerène

par Harry Kroto, prix Nobel de chimie 1996.

Voir Pensées & humour

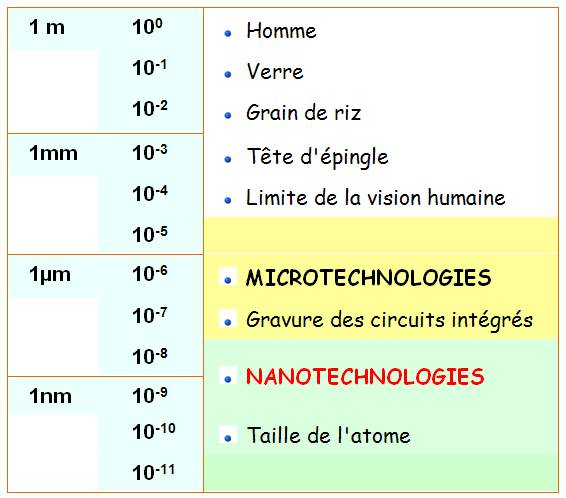
NANOTECHNOLOGIES

ou Nanos

Technologie de l'infiniment petit. La technologie du futur?

En grossissant un million de fois …

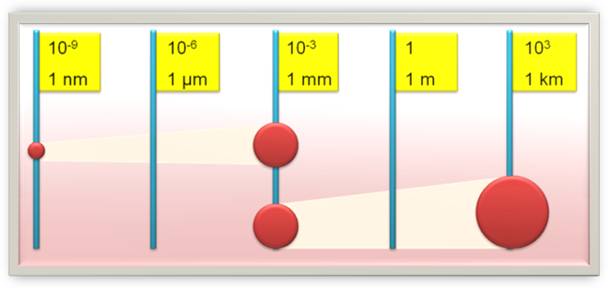
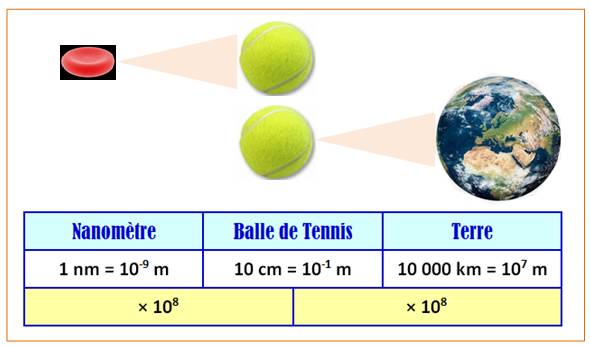
Si une nanoparticule de 1nanomètre (10^-9) devenait une tête d'épingle (1mm), la tête d'épingle agrandie de la même manière aurait une taille de 1 km.

Autre comparaison (ordre de grandeur)

Un nanomètre est à la balle de tennis ce qu'est la balle de tennis à la Terre.

Approximations, car en fait:
Globule rouge: 7 nm; Balle de tennis: 6,5 cm et Terre: 12 742 km

APPROCHE

Voir Échelle de 10 / Très petits nombres  Les nanotechnologies concernent surtout l'électronique, les ordinateurs et l'ingénierie. On imagine des nano robots assemblant des nano éléments qui pourraient reproduire la complexité du vivant qui lui-même serait à même de construire nos équipements: chaise, lait, voiture et ... armes! La nanotechnologie s'étend aussi aux produits de nano-taille dont les propriétés offrent des perspectives inégalées. C'est le cas du fullerène, par exemple.

Tailles comparées

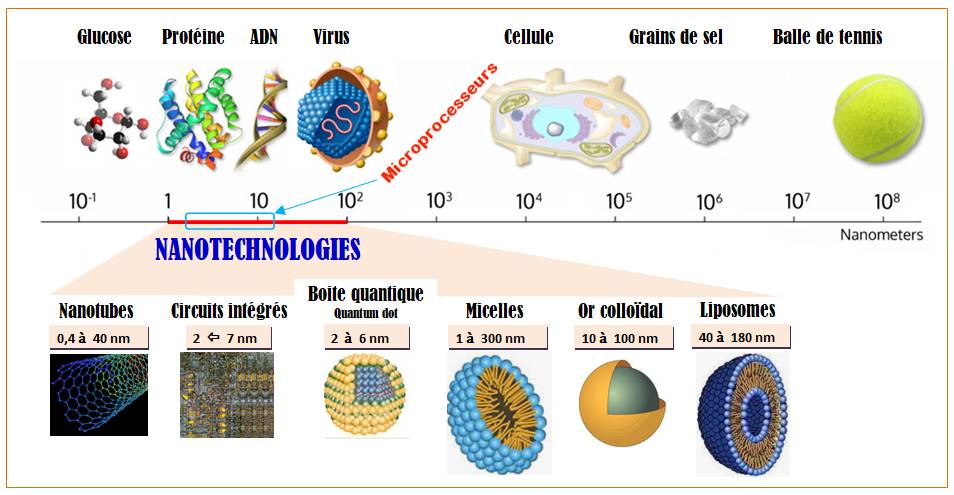
Voir Brève 47-925 / Gravure des microprocesseurs (3 nm en 2022)

Rappel des préfixes

Voir Échelle de 10 (préfixes) / Mnémotechnique

DONNÉES
Nanomètre	= 000 000 001 = 10^-9 mètre = un milliardième de mètre
Nanotechnologie	Industrie de l'extrême miniature.
Nanoscience	Manipulation de la matière à l'échelle de l'atome.
Nanotubes	En carbone, 100 fois plus solide que l'acier et 6 fois plus léger.
Nanotransistors	Le laboratoire de Hewlett-Packard arrive à nicher un transistor dans une molécule.
Marché	1000 milliards de $ en 2015.
Littérature	Michael Crichton (Jurassic Park, Urgences…) vient de faire paraître un roman sur les dangers de la nanoscience: "La Proie". Il met en scène les méfaits de robots intelligents de la taille des molécules.

L'ambition des nanotechnologies est de refaire ce que la vie a fait, mais à notre façon. Jean-Marie Lehn, prix Noble français de chimie.

Les nanotechnologies semblent offrir des outils pour connecter l'inerte au vivant et générer dans la matière des propriétés d'auto-organisation ou de réplication jusqu'ici restées l'apanage des seuls organismes biologiques.

Dorothée Benoit Browaeys

Voir Pensées & humour

Nanoparticules (NPs)

Les nanoparticules sont généralement utilisées en incorporation à d'autres produits pour en augmenter certaines qualités: résistance, souplesse, anti-cassure, conductivité électrique ou thermique … En 2010, elles sont déjà très utilisées dans pratiquement toutes les industries. Nanotubes Feuillets de carbone formant une sorte de grillage enroulé de quelques nanomètres de diamètre. Taille voisine de celle de l'ADN. Ressemble, en miniature, à une gaine de protection de bouteille. Plus résistants, plus flexibles et plus légers que l'acier: cadre de vélo, raquette … Très bonne conductivité électrique même à faible dose: ils sont incorporés dans les plastiques pour permettre la peinture électrostatique des pièces d'automobile, par exemple. Meilleur conductivité thermique, comme le diamant. Par exemple. utilisation pour évacuer la chaleur des circuits électroniques qui deviennent de plus en plus miniatures tout en dissipant autant. Nanoparticules de titane Oxyde de titane (TiO2): pigment blanc pour les peintures, les plastiques, les encres; largement utilisé aussi dans les prothèses dentaires. En nanoparticules, cet oxyde devient transparent et absorbe les ultraviolets: crèmes solaires, produits antivieillissement … Catalyseur (moteur diesel), élimination des oxydes d'azote (revêtement de routes)

Voir Fullerène

HISTORIQUE
1959 Richard Feynman	Plutôt que de diviser sans cesse la matière, pourquoi ne pas partir de l'infiniment petit pour construire quelque chose?
1969 Eric Drexler	Étudiant de Feynman, chercheur au MIT, invente le terme nanotechnologie pour son rapport de stage. Il imagine une nano-usine capable d'assembler des nano-robots.
1985 Gerd Binnig Heinrich Rohrer	Mise au point du microscope à effet tunnel, capable de montrer le 1/25 d'atome. Prix Nobel en 1986.
1990 Don Eigler	Dessine le logo d'IBM quasiment à l'échelle atomique.
En 1990, à 36 ans, Donald Eigler, physicien chez IBM, a réussi à déplacer des atomes de xénon, l'un après l'autre, comme des cubes de Lego. Pour la première fois la matière était manipulée à l'échelle atomique. Explications Pour ce résultat, on utilise un TSM : Scanning-Tunneling Microscope : microscope à effet tunnel. Une pointe métallique explore, à l'échelle atomique, la surface d'un métal conducteur, comme le nickel. Elle est traversée par un courant électrique. En lisant les minuscules variations du flux d'électrons qui se glisse (comme dans un tunnel) entre elle et les atomes de la surface métallique, la pointe produit une image de la surface, comme la pointe d'un phonographe donne naissance à du son. Ce travail est comparable à celui des aveugles qui se font une image mentale d'un objet en l'effleurant.

Danger ou pas?

Rien à craindre pour le moment des nano-robots ou de transhumains faits de chair et de nano-éléments qui deviendraient plus ou moins invincibles ou immortels. Le danger viendrait plutôt des nanoparticules. À l'état libre, elles pourraient pénétrer au travers des tissus humains. Création de mutations cancérigènes? On ne sait pas encore aujourd'hui. Mise au point de smart dust (poussière intelligents), agrégat de minuscules systèmes qui communiquent entre eux, capables de mesurer les paramètres de l'environnement. Capable de prévenir, de guérir … Voire, dans le domaine de la défense, capable de tuer.

NANOPARTICULES dans la nature
L'air contient des nanoparticules issues des poussières d'érosion, des retombées des volcans, des fumées industrielles, des échappements des véhicules … Concentration moyenne: 10 000 /cm^3 Contraction en pic: 700 000 /cm^3

Granularité et surface développée

Plus un grain de matière est découpé finement, plus la surface (l'aire) résultante s'accroît.

Application

Pour un cube de un mètre de côté, la surface développée est de 6 m². Découpons ce cube en cubes de côté 10 fois plus petit (1dcm). Chaque petit cube développe une surface de 6 dcm² ou 0,06m². Mais, il y en a 1000, soit une surface totale de 0,06 x 1000 = 60 m².

Conclusion

En divisant le côté du cube par 10, la surface est multipliée par 10.

En résumé:

Côté du cube	Quantité	Surface
1 m	1	6 m²
1 dcm	1 000	6 dcm² x 100 = 60 m²

Nanoparticules

Granularité	Diamètre divisé par	Surface en mm²	Surface en m²
1 mm	1	3,14	0,000006
1 µm	10^3	3,14 10^3	0,006
1nm	10^6	3,14 10^6	6

Exemple

Un gramme de dioxyde de titane en nanoparticules offre une surface d'interaction de 60 m², contre quelques centimètres carrés lorsqu'il est pulvérulent.

Voir Préfixes milli, micro, nano

Sources: L'Express du 6/11/2003 puis du 2/3/2010

& Livre cité en référence

Voir	Étapes de développement des nanotechnologies Informatique & multimédia Objets invisibles Levier Loi de Moore NBIC Plan 34-2013
DicoNombre	Nanotechnologie en 10^-9
Sites	La découverte du nanomonde Site du Ministère délégué à l'enseignement supérieur et à la recherche - Introduction simple et donnant l'essentiel Impact of Technological Trends and Electromagnetic Compatibility of Integrated Circuits – Etienne Sicard, Alexandre Boyer – 2019
Livres	Le meilleur des nanomondes – Dorothée Benoit Browaeys – Buchet & Chastel – 2009 - Docu-fiction très abordable et particulièrement informatif. Le grand livre des idées reçues – Dominique Vinck pour cette partie – Le Cavalier Bleu – 2010
Cette page	http://villemin.gerard.free.fr/Scienmod/Nanotech.htm