|
||||||||||||||||||||
![]()
|
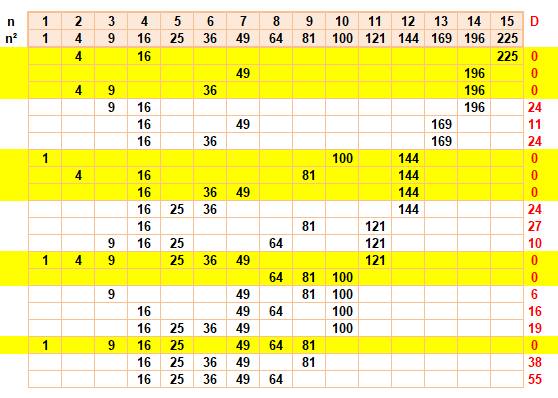
PARTITION en sommes de carrés Toutes
les partitions pour quelques nombres. Les
partitions en carrés distincts pour les nombres de 1 à 100. |
|
|
|
|
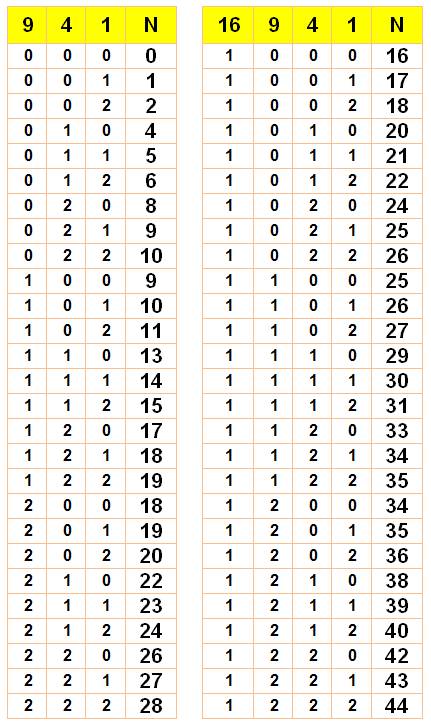
10 = 10 x 1² = 1x2² + 6x1² = 2x2² + 2x1² = 1x3² + 1x1² 9, 4, 1 0 ,
0 , 10 0 ,
1 , 6 0 ,
2 , 2 1 ,
0 , 1 |
|
|
|
|
|
16, 9, 4,
1 0 ,
0 , 0
, 20 0 ,
0 , 1
, 16 0 ,
0 , 2
, 12 0 ,
0 , 3
, 8 0 ,
0 , 4
, 4 0 ,
0 , 5
, 0 0 ,
1 , 0
, 11 0 ,
1 , 1
, 7 0 , 1
, 2 , 3 0 ,
2 , 0
, 2 1 ,
0 , 0
, 4 1 ,
0 , 1
, 0
|
|
|
|
|
|
39 = 39 x 1² = 1x2² + 35x1² = 2x2² + 31x1² 81, 64, 49, 36,
25, 16, 9,
4, 1 0 ,
0 , 0
, 0 ,
0 , 0
, 0 ,
0 , 39 0 ,
0 , 0
, 0 ,
0 , 0
, 0 ,
1 , 35 0 ,
0 , 0
, 0 ,
0 , 0
, 0 ,
2 , 31 0 ,
0 , 0
, 0 ,
0 , 0
, 0 ,
3 , 27 0 ,
0 , 0
, 0 ,
0 , 0
, 0 , 4
,
23 0 ,
0 , 0
, 0 ,
0 , 0
, 0 ,
5 , 19 0 ,
0 , 0
, 0 ,
0 , 0
, 0 ,
6 , 15 0 ,
0 , 0
, 0 ,
0 , 0
, 0 ,
7 , 11 0 ,
0 , 0
, 0 ,
0 , 0
, 0 ,
8 , 7 0 ,
0 , 0
, 0 ,
0 , 0
, 0 ,
9 , 3 0 ,
0 , 0
, 0 ,
0 , 0
, 1 ,
0 , 30 0 ,
0 , 0
, 0 ,
0 , 0
, 1 ,
1 , 26 0 ,
0 , 0
, 0 ,
0 , 0
, 1 ,
2 , 22 0 ,
0 , 0
, 0 ,
0 , 0
, 1 ,
3 , 18 0 ,
0 , 0
, 0 ,
0 , 0
, 1 ,
4 , 14 0 ,
0 , 0
, 0 ,
0 , 0
, 1 ,
5 , 10 0 ,
0 , 0
, 0 ,
0 , 0
, 1 ,
6 , 6 0 ,
0 , 0
, 0 ,
0 , 0
, 1 ,
7 , 2 0 ,
0 , 0
, 0 ,
0 , 0
, 2 ,
0 , 21 0 ,
0 , 0
, 0 ,
0 , 0
, 2 ,
1 , 17 0 ,
0 , 0
, 0 ,
0 , 0
, 2 ,
2 , 13 0 ,
0 , 0
, 0 ,
0 , 0
, 2 ,
3 , 9 0 ,
0 , 0 , 0
, 0 ,
0 , 2
, 4 , 5 0 ,
0 , 0
, 0 ,
0 , 0
, 2 ,
5 , 1 0 ,
0 , 0
, 0 ,
0 , 0
, 3 ,
0 , 12 0 ,
0 , 0
, 0 ,
0 , 0
, 3 ,
1 , 8 0 ,
0 , 0
, 0 ,
0 , 0
, 3
, 2 , 4 0 ,
0 , 0
, 0 ,
0 , 0
, 3 ,
3 , 0 0 ,
0 , 0
, 0 ,
0 , 0
, 4 ,
0 , 3 0 ,
0 , 0
, 0 ,
0 , 1
, 0 ,
0 , 23 0 ,
0 , 0
, 0 ,
0 , 1
, 0 ,
1 , 19 0 , 0
, 0 ,
0 , 0
, 1 ,
0 , 2
, 15 0 ,
0 , 0
, 0 ,
0 , 1
, 0 ,
3 , 11 0 ,
0 , 0
, 0 ,
0 , 1
, 0 ,
4 , 7 0 ,
0 , 0
, 0 ,
0 , 1
, 0 ,
5 , 3 0 ,
0 , 0
, 0 , 0
, 1 ,
1 , 0
, 14 0 ,
0 , 0
, 0 ,
0 , 1
, 1 ,
1 , 10 0 ,
0 , 0
, 0 ,
0 , 1
, 1 ,
2 , 6 0 ,
0 , 0
, 0 ,
0 , 1
, 1 ,
3 , 2 0 ,
0 , 0
, 0 ,
0 , 1
, 2 , 0 , 5 0 ,
0 , 0
, 0 ,
0 , 1 , 2
, 1 , 1 0 ,
0 , 0
, 0 ,
0 , 2
, 0 ,
0 , 7 0 ,
0 , 0
, 0 ,
0 , 2
, 0 ,
1 , 3 0 ,
0 , 0
, 0 ,
1 , 0
, 0 ,
0 , 14 0 ,
0 , 0
, 0 ,
1 , 0
, 0 ,
1 , 10 0 ,
0 , 0
, 0 ,
1 , 0
, 0 ,
2 , 6 0 ,
0 , 0
, 0 ,
1 , 0
, 0 ,
3 , 2 0 ,
0 , 0
, 0 ,
1 , 0
, 1 ,
0 , 5 0 ,
0 , 0
, 0 , 1 , 0
,
1 , 1
, 1 0 ,
0 , 0
, 1 ,
0 , 0
, 0 ,
0 , 3
|
|
|
|
|
|
81, 64, 49, 36,
25, 16, 9,
4, 1 0 ,
0 , 0
, 0 ,
2 , 2
, 1 ,
2 , 1 0 ,
0 , 0
, 0 ,
2 , 2
, 2 ,
0 , 0 0 ,
0 , 0
, 1 ,
1 , 1
, 2 ,
1 , 1 0 ,
0 , 0
, 1 ,
2 , 0
, 1 ,
1 , 1 0 ,
0 , 0
, 2
, 0 ,
0 , 2 , 2
, 2 0 ,
0 , 1
, 0 ,
0 , 2
, 1 ,
2 , 2 0 ,
0 , 1
, 0 ,
0 , 2
, 2 ,
0 , 1 0 ,
0 , 1
, 0 ,
1 , 0
, 2 ,
2 , 0 0 ,
0 , 1
, 0 ,
1 , 1
, 0 ,
2 , 2 0 ,
0 , 1 ,
0 , 1
, 1 ,
1 , 0
, 1 0 ,
0 , 1 , 0
, 2 , 0 ,
0 , 0
, 1 0 ,
0 , 1
, 1 ,
0 , 0
, 1 ,
1 , 2 0 ,
0 , 2 , 0
, 0 , 0 ,
0 , 0
, 2 0 ,
1 , 0
, 0 ,
0 , 1
, 2 ,
0 , 2 0 , 1 ,
0 , 0
, 0 ,
2 , 0
, 1 , 0 0 ,
1 , 0
, 0 ,
1 , 0
, 1 ,
0 , 2 0 , 1 ,
0 , 1
, 0 ,
0 , 0
, 0 , 0 1 ,
0 , 0
, 0 ,
0 , 0
, 1 ,
2 , 2 1 , 0
, 0 , 0 ,
0 , 0
, 2 ,
0 , 1
1 ,
0 , 0
, 0 ,
0 , 1
, 0 ,
0 , 3
Voir Nombre 100 |
|
|
|
|
|
81, 64,
49, 36, 25,
16, 9, 4,
1 1 , =>
, 0 , 0 ,
0 , 0
, 0 ,
0 , 0
, 0 , 1 4 , =>
, 0 , 0 ,
0 , 0
, 0 ,
0 , 0
, 1 , 0 5
, => ,
0 , 0
, 0 ,
0 , 0
, 0 ,
0 , 1 , 1 9 , =>
, 0 , 0
,
0 , 0
, 0 ,
0 , 1
, 0 , 0 10 ,
=> , 0
, 0 ,
0 , 0
, 0 ,
0 , 1
, 0 , 1 13 ,
=> , 0
, 0 ,
0 , 0
, 0 ,
0 , 1
, 1 , 0 14 ,
=> , 0
, 0 ,
0 , 0
, 0 ,
0 , 1 , 1
, 1 16
, => ,
0 , 0
, 0 ,
0 , 0
, 1 ,
0 , 0
, 0 17 ,
=> , 0
, 0 ,
0 , 0
, 0 ,
1 , 0
, 0 , 1 20 ,
=> , 0
, 0 ,
0 , 0
, 0 ,
1 , 0
, 1 , 0 21 ,
=> , 0 , 0
, 0 ,
0 , 0
, 1 ,
0 , 1
, 1 25 ,
=> , 0
, 0 ,
0 , 0
, 0 ,
1 , 1
, 0 , 0 25
, => ,
0 , 0
, 0 ,
0 , 1
, 0 ,
0 , 0
, 0 26 ,
=> , 0
, 0 ,
0 , 0
, 0 , 1
,
1 , 0
, 1 26 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
0 , 0
, 0 , 1 29 ,
=> , 0
, 0 ,
0 , 0
, 0 ,
1 , 1
, 1 , 0 29 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
0 , 0
, 1 , 0 30 ,
=> , 0
, 0 ,
0 , 0
, 0 , 1 ,
1 , 1
, 1 30 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
0 , 0
, 1 , 1 34 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
0 , 1
, 0 , 0 35 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
0 , 1
, 0 , 1 36
, => ,
0 , 0
, 0 ,
1 , 0
, 0 ,
0 , 0
, 0 37 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
0 , 0
, 0 , 1 38 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
0 , 1
, 1 , 0 39 , =>
, 0 ,
0 , 0
, 0 ,
1 , 0
, 1 ,
1 , 1 40 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
0 , 0
, 1 , 0 41 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
1 , 0
, 0 , 0 41 ,
=> , 0
, 0 ,
0 , 1 , 0
, 0 ,
0 , 1
, 1 42 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
1 , 0
, 0 , 1 45 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
1 , 0
, 1 , 0 45 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
0 , 1
, 0 , 0 46 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
1 , 0
, 1 , 1 46 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
0 , 1
, 0 , 1 49 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
0 , 1
, 1 , 0 49
, => ,
0 , 0
, 1 , 0
, 0 ,
0 , 0
, 0 , 0 81, 64,
49, 36, 25,
16, 9, 4,
1 50 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
1 , 1
, 0 , 0 50 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
0 , 1
, 1 , 1 50 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
0 , 0
, 0 , 1 51 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
1 , 1
, 0 , 1 52 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
1 , 0
, 0 , 0 53 ,
=> , 0
, 0 ,
0 , 1 ,
0 , 1
, 0 ,
0 , 1 53 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
0 , 0
, 1 , 0 54 ,
=> , 0
, 0 ,
0 , 0
, 1 ,
1 , 1
, 1 , 0 54 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
0 , 0
, 1 , 1 55 ,
=> , 0
, 0 ,
0 , 0
, 1 , 1
, 1 , 1 , 1 56 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
1 , 0
, 1 , 0 57 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
1 , 0
, 1 , 1 58 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
0 , 1
, 0 , 0 59 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
0 , 1
, 0 , 1 61 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
1 , 1
, 0 , 0 61 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
0 , 0
, 0 , 0 62 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
1 , 1
, 0 , 1 62 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
0 , 0
, 0 , 1 62 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
0 , 1
, 1 , 0 63 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
0 , 1
, 1 , 1 64
, => ,
0 , 1
, 0 ,
0 , 0
, 0 ,
0 , 0
, 0 65 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
1 , 1
, 1 , 0 65 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
0 , 0 , 1
, 0 65 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
1 , 0
, 0 , 0 65 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
0 , 0
, 0 , 1 66 ,
=> , 0
, 0 ,
0 , 1
, 0 ,
1 , 1
, 1 , 1 66 ,
=> , 0 ,
0
, 0 ,
1 , 1
, 0 ,
0 , 1
, 1 66 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
1 , 0
, 0 , 1 68 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
0 , 0
, 1 , 0 69 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
1 , 0
, 1 , 0 69 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
0 , 0
, 1 , 1 70 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
0 , 1
, 0 , 0 70 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
1 , 0
, 1 , 1 71 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
0 , 1
, 0 , 1 73 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
0 , 1
, 0 , 0 74 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
0 , 1
, 1 , 0 74 ,
=> , 0
, 0 ,
1 , 0
, 0 , 1
, 1 ,
0 , 0 74 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
0 , 0
, 0 , 0 74 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
0 , 1
, 0 , 1 75 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
0 , 1
, 1 , 1 75 , => ,
0 , 0
, 1 ,
0 , 0
, 1 ,
1 , 0
, 1 75 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
0 , 0
, 0 , 1 77 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
1 , 0
, 0 , 0 77 ,
=> , 0
, 1 ,
0 , 0
, 0
, 0 ,
1 , 1
, 0 78 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
1 , 0
, 0 , 1 78 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
1 , 1
, 1 , 0 78 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
0 , 0
, 1 , 0 78
,
=> , 0
, 1 ,
0 , 0
, 0 ,
0 , 1
, 1 , 1 79 ,
=> , 0
, 0 ,
1 , 0
, 0 ,
1 , 1
, 1 , 1 79 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
0 , 0
, 1 , 1 80 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
1 , 0
, 0 , 0 81 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
1 , 0
, 1 , 0 81 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
1 , 0
, 0 , 1 81
, => ,
1 , 0
, 0 ,
0 , 0
, 0 ,
0 , 0
, 0 82 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
1 , 0
, 1 , 1 82 ,
=> , 1
, 0 ,
0 , 0
, 0 ,
0 , 0
, 0 , 1 83 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
0 , 1
, 0 , 0 84 ,
=> , 0
, 0 , 1 ,
0 , 1
, 0 ,
1 , 0
, 1 84 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
1 , 0
, 1 , 0 85 ,
=> , 0
, 0 ,
1 , 1
, 0 ,
0 , 0
, 0 , 0 85 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
1 , 0
, 1 , 1 85 ,
=> , 1
, 0 ,
0 , 0
, 0 ,
0 , 0
, 1 , 0 86 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
1 , 1
, 0 , 0 86 ,
=> , 0
, 0 ,
1 , 1
, 0 ,
0 , 0
, 0 , 1 86 ,
=> , 1
, 0 ,
0 , 0
, 0 ,
0 , 0
, 1 , 1 87 ,
=> , 0
, 0 ,
0 , 1
, 1 ,
1 , 1
, 0 , 1 87 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
0 , 1
, 1 , 0 88 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
0 , 1
, 1 , 1 89 ,
=> , 0
, 0 ,
1 , 1
, 0 ,
0 , 0
, 1 , 0 89 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
1 , 1
, 0 , 0 89 ,
=> , 0
, 1 ,
0 , 0
, 1 ,
0 , 0
, 0 , 0 90 ,
=> , 0 , 0
, 0 ,
1 , 1
, 1 ,
1 , 1
, 0 90 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
1 , 0
, 0 , 0 90 ,
=> , 0
, 0 ,
1 , 1
, 0 ,
0 , 0
, 1 , 1 90 ,
=> , 0
, 1 ,
0 , 0
, 0 , 1
,
1 , 0
, 1 90 ,
=> , 0
, 1 ,
0 , 0
, 1 ,
0 , 0
, 0 , 1 90 ,
=> , 1
, 0 ,
0 , 0
, 0 ,
0 , 1
, 0 , 0 91 ,
=> , 0
, 0 ,
0 , 1 , 1
, 1 , 1 ,
1 , 1 91 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
1 , 0
, 0 , 1 91 ,
=> , 1
, 0 ,
0 , 0
, 0 ,
0 , 1
, 0 , 1 93 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
1 , 1
, 1 , 0 93 ,
=> , 0
, 1 ,
0 , 0
, 1 ,
0 , 0
, 1 , 0 94 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
1 , 0
, 1 , 0 94 ,
=> , 0
, 0 ,
1 , 1
, 0 ,
0 , 1
, 0 , 0 94 ,
=> , 0
, 1 ,
0 , 0
, 0 ,
1 , 1
, 1 , 1 94 , =>
, 0 ,
1 , 0
, 0 ,
1 , 0
, 0 ,
1 , 1 94 ,
=> , 1
, 0 ,
0 , 0
, 0 ,
0 , 1
, 1 , 0 95 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
1 , 0
, 1 , 1 95 ,
=> , 0
, 0 ,
1 , 1 , 0
, 0 ,
1 , 0
, 1 95 ,
=> , 1
, 0 ,
0 , 0
, 0 ,
0 , 1
, 1 , 1 97 ,
=> , 1
, 0 ,
0 , 0
, 0 ,
1 , 0
, 0 , 0 98 ,
=> , 0
, 0 ,
1 , 1
, 0 ,
0 , 1
, 1 , 0 98 ,
=> , 0
, 1 ,
0 , 0
, 1 ,
0 , 1
, 0 , 0 98 ,
=> , 1
, 0 ,
0 , 0
, 0 ,
1 , 0
, 0 , 1 99 ,
=> , 0
, 0 ,
1 , 0
, 1 ,
1 , 1
, 0 , 0 99 ,
=> , 0
, 0 ,
1 , 1
, 0 ,
0 , 1
, 1 , 1 99 ,
=> , 0
, 1 ,
0 , 0
, 1 ,
0 , 1
, 0 , 1 100, =>
, 0 ,
0 , 1
, 0 ,
1 , 1
, 1 ,
0 , 1 100, =>
, 0 ,
1 , 0
, 1 ,
0 , 0
, 0 ,
0 , 0 100, =>
, 1 ,
0 , 0
, 0 ,
1 , 0
, 0 ,
1 , 1 |
|
Toutes les partitions
de n jusqu'à 100 en carrés distincts
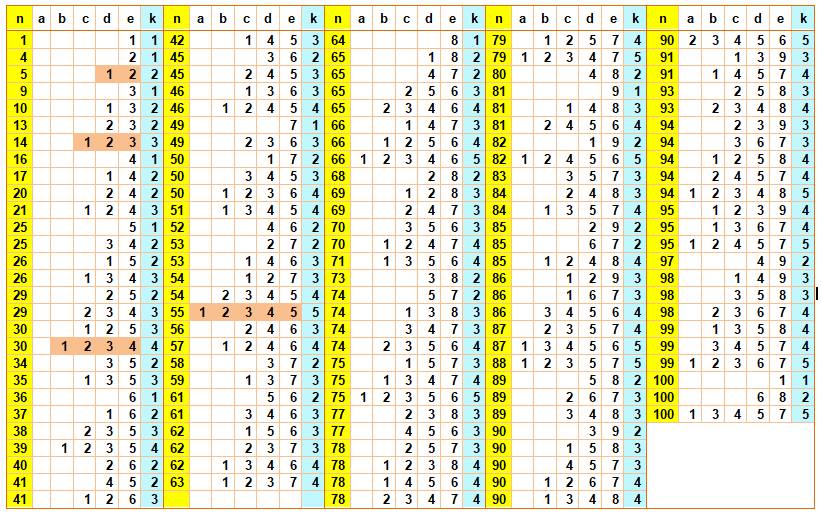
Nombre NON-somme de 1 à 5 carrés de nombres
distincts
|
2, 3, 6, 7, 8,
11, 12, 15, 18, 19, 22, 23, 24, 27, 28, 31, 32, 33, 43, 44, 47, 48, 60, 67,
72, 76, 92, 96, 108, 112, 124, 128,
188. À partir de 189
tous les nombres sont sommes de 1 à 5 carrés distincts. 188 nécessite
six carrés: 188 = 1² + 2² + 3² + 5² + 7² + 10² |
Voir OEIS A1422 / OEIS A003995
Recherche des partitions d'un nombre avec un
tableur
|
Exemple partition de 245: Alignez les carrés successifs, en colonne D, calculez 245 – la somme
sur la ligne des carrés. Partez de 15² = 225 et ajoutez le carré juste
inférieur à la valeur lue en D, continuez jusqu'à obtenir une valeur nulle en
D.
|
Voir Tableur
|
Partitions |
|
|
Le nombre ternaire 102
conduit à 1x9 + 0x4 + 2x1 = 3² + 1² + 1² = 11.
Absents:
3, 7, 12, 32, 37, 41; En double:
9, 10, 17, 19, 20, 22, 24, 25, 27, 34, 35; En triple:
18, 26. |
|
![]()
|
Retour |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/TABLES/aaaParti/Puissanc/carres.htm |
![]()