|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
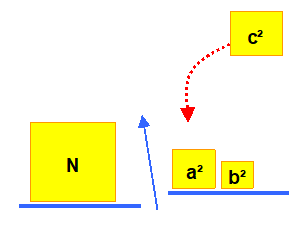
Comprendre les sommes de carrés |
|
|
|
5
= 1² + 1² + 1² +1² + 1² 5
= 2² + 1²
|
|
|
|
|
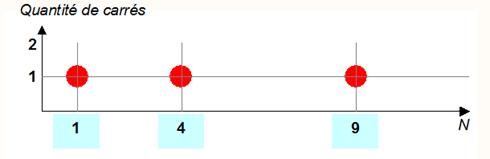
Rappel de la liste
des carrés N 1 2 3 4 5 6 7 8 9 10 … N² 1 4 9 16 25 36 49 64 81 100
Question que l'on se
pose: 4 carrés
sont-ils suffisants lorsqu'on passe à des valeurs plus grandes de N ? Réponse: OUI. |
|
Voir Nombres
carrés
|
|
|
|
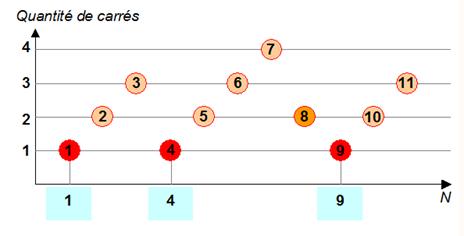
Exemple pour 10
Quantité de carrés
en fonction de N
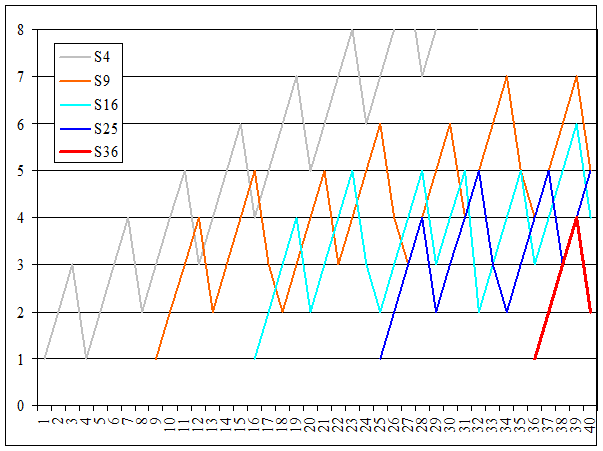
Exemple 18 = 2.3² Deux carrés seulement avec S9. 18
= 1.4² + 2.1² Trois carrés avec la
nouvelle courbe (plus pesante) en S16. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
39
= 6² + 1² + 1² + 1²
39
= 5² + 3² + 2² + 1²
39
= 4² + 4² + 2² + 1² + 1² + 1² |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Que nous appellerons l'empreinte des carrés (ou la
matrice). Empreinte
des carrés
Utilisation
de l'empreinte pour trouver de nouvelles sommes de carrés
Voir Table
de partitions de quelques nombres en sommes de carrés |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Retour |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/PartitiZ.htm |
![]()