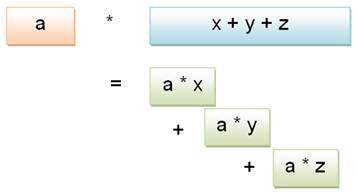|
||||||||||||||||||||||||||||||||||||||||
![]()
|
PARENTHÈSES
|
|
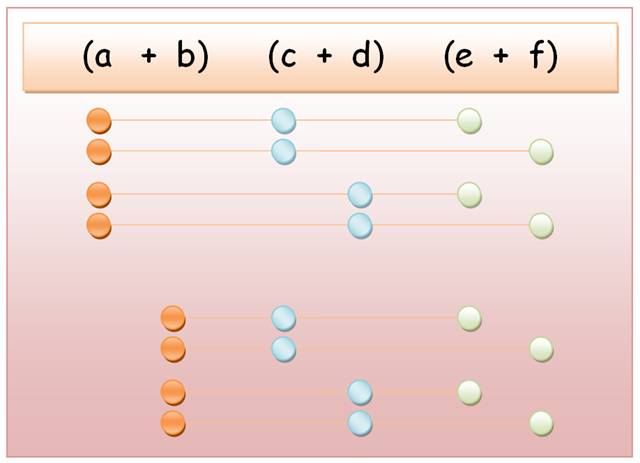
(a+b)(c+d)(e+f)=? |
|
|
Pour
se souvenir:
Au
total, vous conviendrez qu'il y a bel et bien 2 x 3
bonbons et 2 x 5 sucettes.
2
paquets de (3 bonbons + 5 sucettes).
2 (3
bonbons + 5 sucettes) = 6 bonbons et 10 sucettes. Règle
à retenir
A x (B + C) = A x B + A x C
A (B + C) = A B + A C Applications
A (B + C) = A B + A C avec A = (a + b) Je remplace A par sa valeur de chaque côté. (a + b) (B +
C) = (a + b) B
+ (a + b) C Et, discipliné, j'applique à nouveau la
règle (a B + b B)
+ (a C + b C) Bilan: (a + b) (B + C)
= a B + b B + a
C + b C
Solution
du problème posé
E = (a + b) (c + d) (e + f) = ? Pas très compliqué; on va appliquer la
règle en procédant par étapes. Posons X = (a + b) (c + d) Nous savons d'ores et déjà que X = (a + b) (c + d) = ac + ad + bc + bd Notre expression E devient: E = X (e + f) = Xe
+ Xf Remplaçons X par sa valeur E = Xe + Xf = (ac + ad + bc + bd) e + (ac + ad + bc + bd)f On développe en appliquant le terme e à chacun des termes de la parenthèse. Et même chose pour f. E = ace + ade + bce + bde + acf + adf + bcf + bdf Nous y voilà! L'usage veut que l'on mette tout cela par
ordre alphabétique: E = ace + acf
+ ade + adf + bce + bcf + bde + bdf |
|
|
|
||
Illustration
|
||
|
|
|
|
(a + b) (c + d) = ac + ad + bc + bd (a + b) (c + d) (e + f) = ace + acf + ade + adf + bce + bcf + bde +
bdf (a + b) (c + d) (e + f) (g + h) = aceg + aceh + acfg + acfh +
adeg + adeh + adfg + adfh +
bceg + bceh + bcfg + bcfh +
bdeg + bdeh + bdfg + bdfh (a + b) (c + d) (e + f) (g + h) (x + y) = acfhy + acehx
+ bdfhx + adehy + acfhx + acegx + acegy + acehy + acfgx + acfgy + adegx + adegy + adehx + adfgx + adfgy + adfhx + adfhy + bcegx + bcegy + bcehx + bcehy + bcfgx + bcfgy + bcfhx + bcfhy + bdegx + bdegy + bdehx + bdehy + bdfgx + bdfgy + bdfhy
|
|
|
Multi – parenthèses à trois
termes |
|
|
(a + b + c) (d + e + f) = ad +
ae + af + bd + be + bf + cd + ce + cf (a + b + c) (d
+ e + f) (x + y + z) = adx + ady +
adz + aex + aey + aez + afx + afy + afz + bdx + bdy + bdz + bex + bey + bez + bfx + bfy + bfz + cdx + cdz + cex + cey
+ cez + cfx + cfy + cfz + cdy
|
|
|
|
|
|
ace +
abf + abd + acd + acf + abe
abd + abe + abf + acd + ace + acf
a ( bd + be + bf + cd + ce + cf )
a ( b (d + e + f) + c (d + e + f) )
a ( (b + c) (d + e + f) )
a (b + c) (d + e + f) |
|
|
abdx +
abdy + abdz + abdt + abex + abey + abez + abet + abfx + abfy + abfz + abft +
acdx + acdy + acdz + acdt + acex + acey + acez + acet + acfx + acfy + acfz +
acft
= a { bdx + bdy + bdz + bdt + bex + bey + bez + bet + bfx +
bfy + bfz +
bft + cdx + cdy + cdz + cdt + cex + cey + cez + cet + cfx + cfy +
cfz + cft } = a { b (dx + dy + dz + dt
+ ex + ey + ez + et + fx + fy + fz + ft) + c (dx + dy + dz + dt + ex + ey + ez + et + fx + fy + fz
+ ft) } = a { b (dx + dy + dz + dt
+ ex + ey + ez + et + fx + fy + fz + ft) + c (dx + dy + dz + dt + ex + ey + ez + et + fx + fy + fz
+ ft) } = a { ( b + c) (dx + dy
+ dz + dt + ex + ey + ez + et + fx + fy + fz + ft) } = a { ( b
+ c) (d (x + y + z + t)
+ e (x + y + z + t)
+ f (x + y + z + t) } = a { ( b
+ c) (d + e + f ) (x
+ y + z + t) } =
a ( b + c) (d + e + f ) (x + y + z +
t) |
|
|
Base Une
parenthèse indique que son contenu forme un tout, un paquet. Mais il n'est
pas interdit de le déballer. Si
j'ai 3 paquets contenant chacun (2 bonbons et 5 billes), en posant tout cela
sur la table et en regroupant, je constate que j'ai 3 fois 2 bonbons et 3
fois 5 billes. 3 (2bo + 5bi) = 3 x 2 bo + 3 x 5
bi = 6 bo + 15 bi. En algèbre (les boites en couleur représentent des
parenthèses)
Développement: a (x + y + z) = ax
+ ay + az Mise en facteur commun: ax + ay + az = a (x + y + z) Poursuivons Si
(x + y + z) est un
paquet P et que j'en
ai 3 et que l'on m'en donne 7, je peux écrire que j'en ai désormais: 3P + 7P =
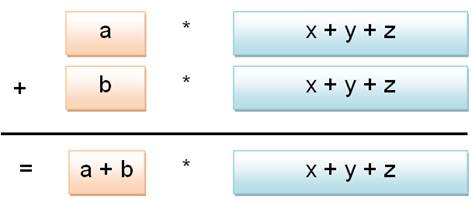
(3 + 7) P = 10 P. En algèbre aP + bP = (a + b) P = (a + b) (x + y + z) Développement: (a + b) (x + y + z) = aP
+ bP = a (x + y + z) + b
(x + y + z)
= ax + ay + az
+ bx + by + bz Règle: on distribue les
termes de la première parenthèse sur tous ceux de la deuxième
Même principe
avec plus de termes
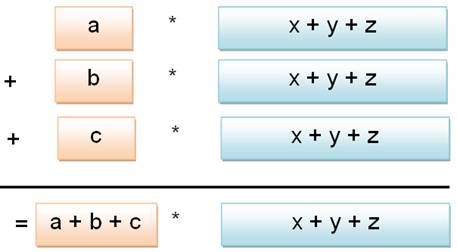
(a +
b + c) ( x + y + z) = a
( x + y + z) + b ( x + y + z) + c ( x + y + z)
= ax
+ ay + az + bx + by + bz + cx + cy + cz Si vous avez un
doute, rassurez – vous avec des nombres: (2 + 3) (4 + 5) =
5 x 9 = 45 = 2x4 + 2x5 + 3x4
+ 3x5 = 8 + 10 + 12 + 15 = 45. |
On
s'en "remet une couche" en développant les identités remarquables
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Voyons le développement des puissances du binôme (a + b)2 = (a
+ b)*(a + b) = aa
+ ab + ba + bb J'ai
distribué a et b
sur les termes de (a + b) = a² +
2ba + b² ab et ba sont deux produits. Ils sont
commutatifs (je peux échanger les termes: ab = ba). (a + b)3 = (a + b)(a + b)(a + b) = (a + b) ( a² + 2ba +
b²) = ( a3 + 2ba² +
ab²) + (ba² + 2ab² + b3) = a3 + 3a²b +
3b²a+ b3 (a + b)4 = (a + b) (a3 + b3 + 3a²b + 3ba²) = a (a3
+ 3a²b + 3ab² + b3) + b (a3
+ 3a²b + 3ab² + b3) = (a4 + 3a 3b + 3a²b² + ab3) + (ba3 + 3a²b² + 3ab3 + b4) Remarque sur les puissances
Décroissance régulière des puissances de a et
croissance régulière des puissances de b. Remarque sur les coefficients
Il est facile de construire la ligne suivante:
chaque nombre est la somme des deux du dessus. C'est le triangle de Pascal. Avec lui, il est possible de développer la
puissance quelconque d'un binôme sans faire le calcul explicite (développement du binôme). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
![]()