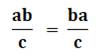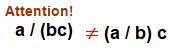base de l'algèbre: les parenthèses

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/02/2023 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	ALGÈBRE
Débutants Algèbre	BASES				Glossaire Algèbre
INDEX Arithmétique et Algèbre Résolution de Problèmes	Techniques de base		Additions	Multiplications
	Parenthèses		Multi Parenthèses	Divisions
	Priorité des opérations
		Sommaire de cette page >>> Un cas de conscience entre parenthèses … >>> Approche >>> Emploi des parenthèses >>> Récapitulatif >>> Exemples >>> Anglais >>> Exemples de problèmes posés sur le Net

PARENTHÈSES

Les parenthèses sont utilisées pour isoler un groupe de symboles à considérer comme un tout.

Elles sont là pour éviter les confusions. Elles facilitent les calculs. On les traite en premier.

Comment les manipuler ? Que vaut: (a + b) (b + c) ?

Anglais: parentheses ( ), brackets [ ] or braces { }

Pour commencer voir: Initiations aux Opérations arithmétiques /

Maths 5^e / Mnémotechnique de la priorité des opérations

Pour mise en bouche

Quelle est la moitié de 2 + 2 ? Ben… c'est ½ x 2 + 2 = 1 + 2 = 3.

Vous avez dit 3, c'est que vous avez oublié de mettre mentalement des parenthèses: moitié de (2 + 2) = ½ (2 + 2) = ½ de 4 = 2.

Remarquez que, à l'oral, l'une ou l'autre réponse est valable selon que deux plus deux est prononcé d'une traite ou avec un temps d'arrêt.

G + R (A + 1) = G + RA + R => G RA R => Gérard

Voir Pensées & humour / Prénoms amusants

Calculez: P = (x – a) (x – b) … (x – z).

Ne vous précipitez pas à effectuer le calcul.

Réponse: parmi tous les facteurs l'un sera (x – x) = 0

Alors P = 0.

Voir Pensées & humour

APPROCHE
ADDITIONS Tous les termes peuvent s'écrire les uns à la suite des autres et sans ordre. Il n'est pas utile d'isoler des groupes de termes.	a + b + c	= b + a + c
SOUSTRACTIONS Tous les termes peuvent s'écrire les uns à la suite des autres et sans ordre. À condition que chaque terme conserve son signe.	a – b – c	= – b + a – c
MULTIPLICATIONS Tous les facteurs peuvent s'écrire les uns à la suite des autres et sans ordre. Il n'est pas utile d'isoler des groupes de termes.	a . b . c abc	= b . c . a = bca
Notes: On peut supprimer le point indiquant la multiplication, s'il n'y a pas d'ambigüité. Pour les puristes: le point de la multiplication est au milieu de la ligne:
DIVISIONS Il est prudent de conserver le bon ordre. Même si les facteurs des produits peuvent être échangés.	a . b / c	= b . a / c
On peut supprimer le point indiquant la multiplication, s'il n'y a pas d'ambigüité.	ab / c	= ba / c
On préférera la forme fractionnaire.

Utilisés seuls:

les + et x forment des chaînes dociles: ordre quelconque; et

les – et / sont moins dociles: vigilance, surtout pour la division.

Voir Détails sur les règles de priorités des opérateurs arithmétiques

EMPLOI DES PARENTHÈSES Opérations seules
ADDITIONS Les parenthèses sont généralement inutiles. Si une expression entre parenthèses est précédée du signe + la parenthèse est inutile.	a + (b + c)	= a + b + c
DIVISION Les parenthèses sont nécessaires. Ne pas tenter de les éliminer! Leur emploi, même en abondance, évite les confusions possibles.
	a / b c	à éliminer car confusion possible entre (a / b) c ou a / (bc)
	Voir Exemples de ces cas ambigus

EMPLOI DES PARENTHÈSES

Opérations composées

Les parenthèses trouvent toute leur justification lorsque diverses opérations sont utilisées dans la même expression.

FACTEUR D'ADDITION

Le facteur commun est placé devant la parenthèse.

Pour développer il faut attribuer ce facteur commun à chacun des termes de la parenthèse.

Image

1 paquet de 2 caramels et 3 chocolats.

Avec 2 paquets nous serons en possession de 4 caramels et de 6 chocolats.

a (b + c)

2 (2ca + 3 ch)

= ab + ac

= 4ca + 6ch

MULTIPLICATION D'ADDITIONS

Pas si compliqué: appliquons la même chose que ci-dessus.

Notez l'astuce (a + b) = (P) pour mieux se rendre compte de ce qui se passe.

(a + b) (c + d)

(P) (c + d)

= (P) c + (P) d

= (a+ b) c + (a + b) d

= ac + bc + ad + bd

Voir illustration en Tracas de calculs avec parenthèses

Voir Produit cartésien

RÉCAPITULATIF selon la quantité de termes
Qté	Parenthèses inutiles	Parenthèses UTILES
2	a + b ab
3	a + b + c a + bc abc	a	(b + c)	= ab + ac
4	a + b + c + d a + bcd ab + cd abcd	a ab (a + b)	(b + c + d) (c + d) (c + d)	= ab + ac + ad = abc + abd = ac + bc + ad + bd

BILAN

On effectue les calculs d'abord à l'intérieur des parenthèses.

La multiplication est prioritaire sur l'addition.

P (c + d) = Pc + Pd même si P est une expression comme (a + b).

EXEMPLES – Enlever les parenthèses inutiles
a + 2 b + (2a – 3b) = a + 2 b + 2a – 3b
a + 2 b - (2a – 3b) = a + 2 b - 2a + 3b
{3a + 2b + (2a – 6b) – [3a – (2x + 4y) + z] – 6t} = {3a + 2b + 2a – 6b – [3a – 2x - 4y + z] – 6t} = {3a + 2b + 2a – 6b – 3a + 2x + 4y - z – 6t} = 3a + 2b + 2a – 6b – 3a + 2x + 4y - z – 6t = 2b + 2a – 6b + 2x + 4y - z – 6t
3(x – 2y) + 2 (x + 4y) = 3x – 6y + 2x + 8y = 5x + 2y
3(x – 2y) – 2 (x - 4y) = 3x – 6y – 2x + 8y = x + 2y
4x +3{ x – (1 – y) + 2(1 – x) } = 4x + 3{ x – 1 + y + 2 – 2x } = 4x + 3x – 3 + 3y + 6 – 6x = x + 3y + 3
4x -3{ x – (1 – y) + 2(1 – x) } = 4x - 3{ x – 1 + y + 2 – 2x } = 4x - 3x + 3 - 3y - 6 + 6x = 10x – 3y - 3
(2a + 3b + c) (x + y + z) = 2a (x + y + z) + 3b (x + y + z) + c (x + y + z) = 2ax + 2ay + 2az + 3bx +3by + 3bz + cx + cy + cz

ENGLISH CORNER

Brackets are used to indicate that the terms enclosed within them are to be considered as one entity.

Cas de conscience qui montrent l'importance des parenthèses …

On trouve des énigmes mathématiques sur Internet sous le nom: cette équation va vous rendre complètement fou ! Les Anglo-Saxons parlent aussi de problèmes viraux sur le Net ou de problèmes qui affolent le Net.

Comme ce cas: 82(2+2) = 1 ou 16 ?