|
||||||||||||||||||||||||||||||||||||||||
![]()
|
ADDITION & SOUSTRACTION Un peu de méthode et le travail est plus
simple et plus sûr. |
Voir Bases
telles qu'enseignées en 5e
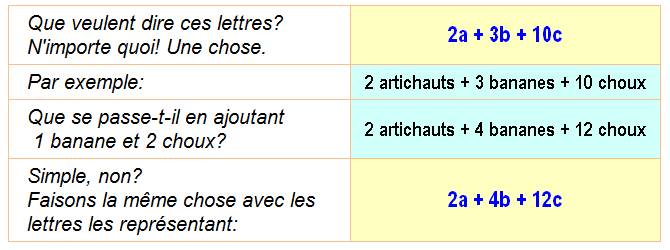
Je ne comprends pas
pourquoi, on met des lettres.
|
|
||||||||||
|
|
(3a
+ 2b – 5c) + (4a – b + c – 5d) |
|||||||||
|
|
3a
+ 2b – 5c + 4a – b + c – 5d |
|||||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
|
7a
+ b – 4c – 5d |
|||||||||
|
EXEMPLES |
|
|||||||||
|
Un petit piège! |
||||||||||
|
|
(3a
+ 2b – 5c) + (–4a – b + c – 5d) |
|||||||||
|
|
3a
+ 2b – 5c – 4a – b + c – 5d |
|||||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
Un plus gros piège! |
||||||||||
|
|
(3a
+ 2b – 5c) – (4a – b + c – 5d)
|
|||||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
Un très gros piège |
||||||||||
|
|
(3a
+ 2b – 5c) – (–
4a – b + c – 5d) |
|||||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
|
||||||||||||||||||||||||||
|
Regrouper
les objets de même type |
||||||||||||||||||||||||||
|
|
(5abc + 2cd + 2ab – 7y – xyz) + (5x – ab + 8y + 4xyz) –(2abc + cd + xyz) |
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
Il
est d'usage d'ordonner par puissances décroissantes |
||||||||||||||||||||||||||
|
|
(4x3
+ 3x4 – 5x2 –
10x + 13 + x5) +
(5x2 – 2x3 – 10 – 10x) +
(2x3 + x2 + 3x4 + 4x5) +
(3x4 + 2x2 + 1) |
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
Puissances
croissantes et décroissantes |
||||||||||||||||||||||||||
|
|
(5x3
– 4xy2 + 2x2y – y3) +
(2x2y – 2x3) +
(10y3 + 9xy2 + 2x2y) +
(2x2y – 4xy2 – y3 –2x3) |
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
Pour un mathématicien,
calculer c'est raisonner, c'est analyser plus profondément les faits
géométriques sous-jacents; pour un jeune élève, calculer c'est laisser aux
symboles le soin de raisonner à sa place, c'est oublier tout fait géométrique
pour ne plus voir que des symboles. Henri
Lebesgue |
Voir
Pensées & humour
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()
