NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/02/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Puissances
Débutants Pythagore Débutants Pythagore – Diaporama	Opérations sur les puissances		Glossaire Puissances
Rubrique PARTITION INDEX PUISSANCES	Somme de puissances
	Th de Pythagore	Th de Fermat-Wiles
	Démonstration du théorème	Carré somme de cubes
	Sommaire de cette page >>> Plus petites solutions pour n = 1 >>> Table des records >>> Tous les nombres >>> Certains nombres >>> Propriétés: résumons ce que nous savons

SOMME DE PUISSANCES

Introduction à la rubrique Pythagore et Fermat où il est question d'un nombre N à la puissance p égal à r nombres à la même puissance p. C'est un problème de partition avec des puissances.

On cherche à connaitre les plus petites configurations.

Exemple:

Spnm = S514 est la plus petite somme avec des puissances p = 5 avec n = 1 terme à gauche et m = 4 termes à droite. Notez qu'il a seulement quatre termes pour une puissance 5.

Pour rubrique avancée sur les sommes des puissances

Voir S'y retrouver

Plus petites solutions pour n = 1 (un seul terme à gauche)
On connait les triplets de Pythagore, une infinité.	S212	5² = 4² + 3²
On sait qu'il n'existe aucune somme S3nm: théorème de Fermat-Wiles.	S312	a^k = b^k + c^k Aucune solution
Si on ajoute un terme, on a des solutions	S313	6^3 = 5^3 + 4^3 + 3^3
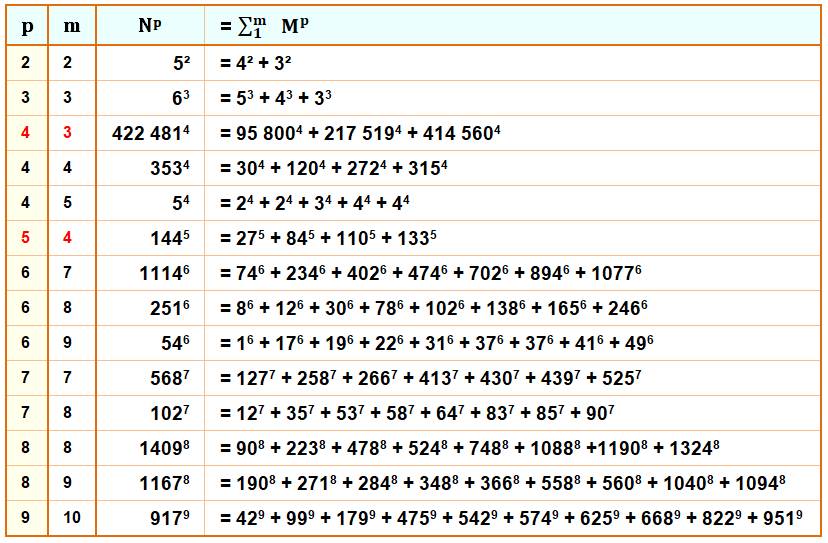
Avec les ordinateurs, les recherches sont nombreuses et on peut entretenir une liste des configurations les plus petites. La table indique la valeur minimale de N dans chaque cas. Le premier cas pour chaque p est un record: il n'existe pas de possibilité avec moins de termes (m) pour cette puissance. Notez les rares cas (en rouge) où la quantité de termes est inférieure au degré de la puissance. Plus p est grand et plus m le surpasse largement (p = 32, plus petite valeur connue m = 230).

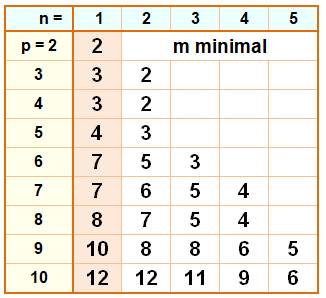
Records pour Sp1m avec p jusqu'à 9

Référence et plus sur Euler's Sum of PowersConjecture – Wolfram MathWorld

Bilan des connaissances actuelles

Récapitulatif des records: pour une puissance p donnée et une quantité n de termes à gauche, combien (m) de termes à droite au minimum. Exemple: la colonne ocre montre les cas vus ci-dessus. Une puissance 5 est égale à 4 puissances 5 au moins. Dans la deuxième colonne: la somme de deux puissances 5 est égale à au moins 3 puissance 5.

Tableau complet Computing Minimal Equal Sums Of Like Powers – Jean-Charles Meyrignac

Revue de détail

TOUT NOMBRE …
4P2: Tout nombre peut s'écrire comme une somme d'au plus 4 puissances 2 (carrés).	12 = 2² + 2² + 2² 7 = 2² + 1² + 1² + 1²
9P3: Tout nombre peut s'écrire comme une somme d'au plus 9 puissances 3 (cubes).	36 = 3^3 + 2^3 + 1^3 10 = 2^3 + 1^3 + 1^3
19P4: Tout nombre peut s'écrire comme une somme d'au plus 19 puissances 4 (bicarrés).	434 = 2^4 + 3^4 + 3^4 + 4^4
Tout nombre peut s'écrire comme une somme d'au plus k puissances p. Théorème de Waring	N = a1 ^p + a2 ^p + …

Résumons la situation en tableau. pout tout nombre:
Quantité de termes dans la somme	Carrés	Cubes	Bicarrés
3
4	4P2	Il existe de nombreux
5		cas
…
9		9P3
…	TOUS
19	Toujours		19P4
…

NOMBRES puissance, somme de puissances
Certains nombres	peuvent s'écrire comme	Exemples
Carrés	somme de 2 carrés	5² = 4² + 3²
	somme de 3 carrés	13² = 3² + 4² + 12²
Cubes	somme de 3 cubes	6^3 = 5^3 + 4^3 + 3^3 9^3 = 8^3 + 6^3 + 1^3
Bicarrés	somme de 4 bicarrés	353^4 = 30^4 + 120^4 + 272^4 + 315^4
	somme de 3 bicarrés Euler le pensait impossible	422 481^4 = 95 800^4 + 217 + 519^4 + 414 560^4
Mais
Cube	somme de 2 cubes	IMPOSSIBLE
Bicarrés	somme de 2 bicarrés	IMPOSSIBLE

Résumons ce que nous savons
Quantité de termes dans l'addition	Carrés	Cubes	Bicarrés	Puissance 5 et plus
2* triplets	OUI Une infinité PYTHAGORE	IMPOSSIBLE FERMAT
3 quadruplets	3² + 4² + 12² = 13²	5^3 + 4^3 + 3^3 = 6^3	Existe EULER	? On ne sait pas encore
4 quintuplets		Il existe des cas		Existe EULER
…	TOUS WARING
9

* deux termes dans l'addition; trois termes dans la relation d'où le nom de triplet.

Principales propriétés
Pythagore (théorème)	Infinité de triplets: carré = somme de 2 carrés.	De très nombreuses démonstrations.
Fermat (théorème)	Aucune somme de deux mêmes puissances ne donne un nombre à cette puissance sauf pour la puissance 2.	Démontré par Andrew Wiles en 1994.
Euler (conjecture)	Aucune somme de k – 1 mêmes puissances k ne donne un nombre à cette puissance.	Conjecture fausse Contre-exemple en 1966 par ordinateur
Waring (théorème)	Tout nombre est décomposable en une quantité maximum de puissances k.	Démontré

Suite	Th de Pythagore
Voir	S'y retrouver Pythagore - Biographie Addition - Glossaire Années Pythagore Décade de Pythagore Partitions Nombre = sommes de puissances
Sites	Computing Minimal Equal Sums Of Like Powers – Jean-Charles Meyrignac Euler's Sum of PowersConjecture – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThPyFer.htm